Головна ⇒ 📌Плани-конспекти уроків по математиці ⇒ Формули зведення

Формули зведення

УРОК 14

Тема. Формули зведення

Мета уроку: вивчення формул зведення, формування умінь учнів застосовувати вивчені формули для спрощення ви­разів та обчислень.

І. Перевірка домашнього завдання

1. Відповіді на питання учнів, що виникли в процесі виконан­ня домашнього завдання.

2. Самостійна робота.

1. Спростіть 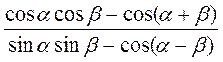Формули зведення. (3 бали)

2. Знайдіть tg 2?, якщо tg? = – 0,4. (3 бали)

3. Спростіть 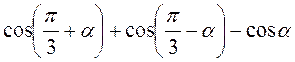Формули зведення. (3 бали)

4. Обчисліть 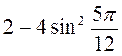Формули зведення. (З бали)

1. Спростіть 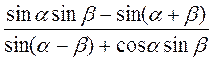Формули зведення. (3 бали)

2.

Знайдіть tg 2?, якщо tg? = 6. (3 бали)

3. Спростіть 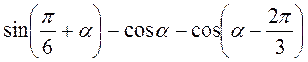Формули зведення. (3 бали)

4. Обчисліть 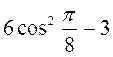Формули зведення. (3 бали)

Відповідь: В-1. 1. – tg? tg?. 2.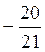Формули зведення. 3. 0. 4. Формули зведення.

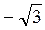В-2. 1. – сtg? tg?. 2. 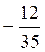Формули зведення. 3. 0. 4. Формули зведення.

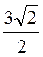II. Сприймання і усвідомлення формул зведення

Тригонометричні функції чисел виду 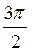Формули зведення ± ?, ? ± ?; Формули зведення ± ?, 2? ± ? можуть бути виражені через функції кута? за допомогою формул, які називаються формулами зведення.

Користуючись формулами тригонометричних функцій суми (різниці) двох чисел, можна

довести формули зведення:

Для синуса

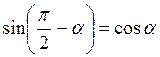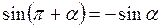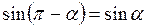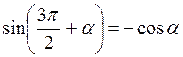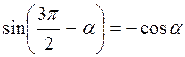, Формули зведення, Формули зведення,

Формули зведення, Формули зведення, Формули зведення.

Для косинуса

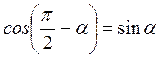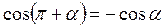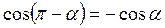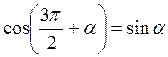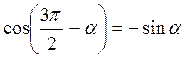, Формули зведення, Формули зведення,

Формули зведення, Формули зведення, Формули зведення.

Для тангенса і котангенса

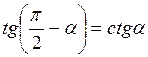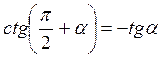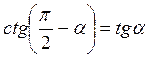, Формули зведення,

Формули зведення, Формули зведення.

Формули зведення запам’ятовувати необов’язково. Для того щоб записати будь-яку з них, можна користуватися таким прави­лом:

1) В правій частині формули ставиться той знак, який має ліва частина при умові 0 < ? < Формули зведення.

2) Якщо в лівій частині формули кут дорівнює 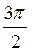Формули зведення ± ?, Формули зведення ± ?, то синус замінюється на косинус, тангенс – на котангенс і на­впаки. Якщо кут дорівнює? ± ?, то заміна не виконується.

Розглянемо приклади.

Приклад 1. Виразимо tg(? – ?) через тригонометричну функцію кута?. Якщо вважати, що? – кут І чверті, то? – ? буде кутом II чверті. У II чверті тангенс від’ємний, отже, у правій частині рівності слід поставити знак “мінус”. Для кута? – ? назва функції “тангенс” зберігається. Тому tg (? – ?) = – tg?.

За допомогою формул зведення знаходження значень триго­нометричних функцій будь-якого числа можна звести до знаходження значень тригонометричних функцій чисел від 0 до Формули зведення.

Приклад 2. Знайдемо значення sіn 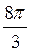Формули зведення.

Маємо: 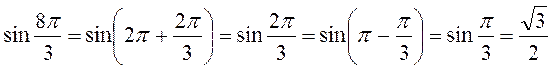Формули зведення.

Виконання вправ______________________________

1. Приведіть до тригонометричних функцій числа а:

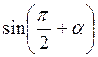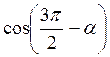А)Формули зведення; б)Формули зведення; в) сtg (? – ?); г) tg (? + ?); д) sіn (? + ?); є)Формули зведення.

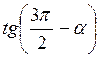Відповідь: а) соs?; б) – sіn?; в) – ctg?; г) tg?; д) – sіn?; є) сtg?.

2. Знайдіть:

А) sіn 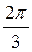Формули зведення; б) соs 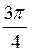Формули зведення; в) tg 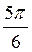Формули зведення; г) sіn Формули зведення.

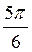Відповідь: а) 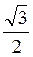Формули зведення ; б) – 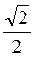Формули зв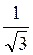едення; в) – Формули зведення; г) Формули зведення.

3. Спростіть:

А) 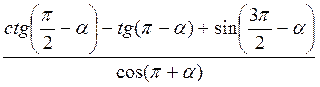Формули зведення; б) Формули зведення.

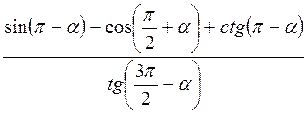Відповідь: а) 1. б) -1.

4. Доведіть, що

А) 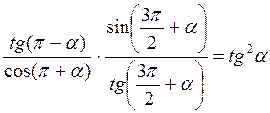Формули зведення, б) Формули зведення.

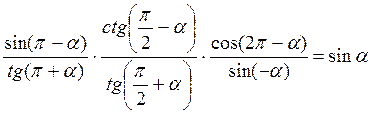III. Підведення підсумків уроку

IV. Домашнє завдання

Розділ І § 10 (2). Запитання і завдання для повторення до розділу І № 66. Вправи № 52 (12), № 26.


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і по­ловинного аргументу УРОК 13 Тема. Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і по­ловинного аргументу Мета уроку: вивчення формул тригонометричних функцій суми і різниці двох чисел, формул тригонометричних функцій подвійного і половинного аргументу. Фор­мування умінь застосовувати вивчені формули для спрощення виразів та обчислень. І. Перевірка домашнього завдання Розв’язання вправ, аналогічних до домашніх: вправа […]...

  2. Формули суми (різниці) однойменних тригономет­ричних функцій. Перетворення добутку тригономет­ричних функцій у суму УРОК 15 Тема. Формули суми (різниці) однойменних тригономет­ричних функцій. Перетворення добутку тригономет­ричних функцій у суму Мета уроку: вивчення формул суми і різниці однойменних три­гонометричних функцій і формул перетворення до­бутку тригонометричних функцій у суму. Формування умінь учнів застосовувати вивчені формули для спро­щення виразів та обчислень. Обладнання. Таблиця “Формули перетворення суми в добуток (добутку в суму)”. І. […]...

  3. Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60°. Розв’язування задач Урок № 58 Тема. Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60°. Розв’язування задач Мета: закріпити знання учнями змісту формул доповнення та числових значень тригонометричних функцій кутів 30°, 45°, 60°. Сформувати вміння застосовувати формули до розв’язування задач. Тип уроку: застосування знань, умінь та навичок. Наочність та обладнання: конспект 22. Хід уроку I. Організаційний етап […]...

  4. Розв’язування тригонометричних рівнянь способом зведення до однієї тригонометричної функції УРОК 23 Тема. Розв’язування тригонометричних рівнянь способом зведення до однієї тригонометричної функції Мета уроку: формування умінь учнів розв’язувати тригонометричні рівняння способом зведення до однієї тригонометричної функції (алгебраїчний спосіб). І. Перевірка домашнього завдання 1. Відповіді на питання, що виникли у учнів при виконанні домашніх завдань. 2. Самостійна робота. Розв’яжіть рівняння: A) cosx = . (3 бали) […]...

  5. Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60° Урок № 57 Тема. Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60° Мета: сформувати в учнів свідоме розуміння змісту та доведення теореми, що містить формули доповнення, а також наслідку з неї; домогтися засвоєння учнями способу обчислення та значень тригонометричних функцій кутів 30°, 45° і 60°. Закріпити знання вивчених формул та сформувати вміння їх застосовувати […]...

  6. Формули подвійного і потрійного аргументу – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули подвійного і потрійного аргументу Для будь-якого α Якщо Якщо...

  7. Формули половинного аргументу – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули половинного аргументу Для будь-якого α Якщо α ≠ (2к +1)π, то Якщо α ≠ 2kπ, то Для тангенса й котангенса половинного аргументу є ще й інші формули, що не містять радикалів. Якщо α ≠ (2к +1)π, то Якщо α ≠ 2kπ, то...

  8. Формули перетворення добутків у суми – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули перетворення добутків у суми Для будь-яких α і β...

  9. Розподільна властивість множення. Зведення подібних доданків Урок № 88 Тема. Розподільна властивість множення. Зведення подібних доданків Мета: завершити роботу з відпрацювання навичок використання розподільної властивості множення для: а) обчислень; б) розкриття дужок; в) зведення подібних доданків; г) винесення найбільшого спільного множника за дужки. Тип уроку: застосування знань, умінь та навичок. Хід уроку I. Перевірка домашнього завдання Усні вправи 1. Обчисліть, використовуючи […]...

  10. Формули зниження степеня – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули зниження степеня Для будь-якого α Якщо , то Якщо α ≠ kπ, то...

  11. Формули перетворення сум у добутки – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули перетворення сум у добутки Для будь-яких α і β...

  12. Формули додавання – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули додавання Для будь-яких α, β Для будь-яких α й β, якщо то А якщо то...

  13. Ділення багатоцифрових чисел, що закінчуються нулями. Ускладнені задачі на зведення до одиниці (№№ 688-696) Тема. Ділення багатоцифрових чисел, що закінчуються нулями. Ускладнені задачі на зведення до одиниці (№№ 688-696). Мета. Ознайомити учнів із діленням багатоцифрових чисел, що закінчуються нулями; закріплювати вміння ділити багатоцифрові числа на одноцифрові; вправляти учнів у розв’язуванні задач на зведення до одиниці; дати поняття про знаходження площі поверхні куба. Обладнання. Таблиця для усних обчислень; завдання для […]...

  14. ПОВТОРЕННЯ ТАБЛИЦІ МНОЖЕННЯ І ДІЛЕННЯ ЧИСЕЛ НА 8. ЗАДАЧІ НА СПОСІБ ЗВЕДЕННЯ ДО ОДИНИЦІ (другий вид) Мета: формувати вміння розв’язувати задачі на спосіб зведення до одиниці; закріпити навички табличного множення і ділення на 8; навчати використовувати вивчений матеріал під час розв’язування задач і прикладів; розвивати обчислювальні навички, логічне мислення, математичне мовлення; виховувати самостійність. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Перевірка домашнього завдання 2. Гра “Ерудит” – Що […]...

  15. Використання формул скороченого множення для розкладання багаточленів на множники. Формули скороченого множення Урок № 50 Тема. Використання формул скороченого множення для розкладання багаточленів на множники. Формули скороченого множення Мета: відпрацювати навички класифікації виразів та застосування формул скороченого множення для розкладання багаточленів та цілих виразів на множники та розв’язування вправ, що передбачають виконання цих Дій; повторити способи дій у разі використання формул скороченого множення для перетворення цілих виразів […]...

  16. Числові і буквені вирази. Формули. Властивості додавання і віднімання УРОК 26 Тема. Числові і буквені вирази. Формули. Властивості додавання і віднімання Мета: закріпити знання учнів про основні поняття теми (числові і буквені вирази, формули, значення числового виразу); продовжувати відпрацьовувати навички складання і знаходження значень буквених виразів при зазначених значеннях змінних, повторити тему “Додавання і віднімання”; підготовити учнів до тематичної контрольної роботи № 2. Тип […]...

  17. Числові і буквені вирази. Формули УРОК 25 Тема. Числові і буквені вирази. Формули Мета: сформувати уявлення учнів про формули як ключ до розв’язання цілого класу задач; продовжувати формування вмінь учнів знаходити значення буквених виразів, а також читати їх і складати буквені вирази за умовою задачі. Тип уроку: засвоєння навичок та вмінь. Обладнання: таблиця-схема “Формули. Вирази”. Хід уроку І. Перевірка домашнього […]...

  18. ДОДАВАННЯ КРУГЛИХ ТРИЦИФРОВИХ ЧИСЕЛ З ПЕРЕХОДОМ ЧЕРЕЗ РОЗРЯД ВИДУ 380 + 590. РОЗШИРЕНА ЗАДАЧА НА ЗВЕДЕННЯ ДО ОДИНИЦІ (другий вид) Мета: ознайомити учнів з усним додаванням круглих трицифрових чисел з переходом через розряд; формувати вміння розв’язувати розширені задачі на зведення до одиниці; розвивати мислення, увагу; виховувати інтерес до математики. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Перевірка домашнього завдання 2. Гра “Шифрувальник” (с. 87, завдання 554) – Розшифруйте слово, розставивши букви в […]...

  19. ЗАДАЧІ НА СПОСІБ ЗВЕДЕННЯ ДО ОДИНИЦІ (другий вид). ВИДИ ТРИКУТНИКІВ Мета: формувати вміння розв’язувати задачі на спосіб зведення до одиниці (другого виду); розвивати вміння розрізняти трикутники за їх кутами; вдосконалювати обчислювальні навички, логічне мислення, математичне мовлення; виховувати старанність. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Перевірка домашнього завдання 2. Гра “Хто швидше?” (с. 39, завдання 273) 3. Фронтальне опитування 1) С. 40, […]...

  20. ЗАДАЧІ НА СПОСІБ ЗВЕДЕННЯ ДО ОДИНИЦІ (перший вид). ДІЇ З ІМЕНОВАНИМИ ЧИСЛАМИ Мета: формувати вміння учнів розв’язувати задачі на спосіб зведення до одиниці; закріпити знання табличних випадків множення і ділення; вдосконалювати вміння виконувати перетворення іменованих чисел; розвивати обчислювальні навички, мислення; виховувати старанність. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Перевірка домашнього завдання 2. Гра “Хто швидше?” Усні обчислення за завданням 199 (с. 30). 3. […]...

  21. Ділення іменованих чисел. Ускладнені задачі на зведення до одиниці (№№ 697-705) Тема. Ділення іменованих чисел. Ускладнені задачі на зведення до одиниці (№№ 697-705). Мета. Вчити учнів ділити іменовані числа, правильно виконувати записи; удосконалювати вміння розв’язувати задачі, складати та обчислювати вирази. Обладнання. Таблиця “Ділення іменованих чисел”; картки для опитування; схеми задач. Зміст уроку I. Контроль, корекція та закріплення знань. 1. Перевірка домашнього завдання. А) Зачитати відповідь до […]...

  22. МНОГОЧЛЕН. ПОДІБНІ ЧЛЕНИ МНОГОЧЛЕНІВ ТА ЇХ ЗВЕДЕННЯ Дата – навчальна: сформувати поняття многочлена, подібних членів многочлена; сформувати вміння зводити подібні члени многочлена; – розвивальна: розвивати творчі здібності, кмітливість учнів; формувати вміння орієнтуватися у видозміненій ситуації; _ – виховна: виховувати зацікавленість у пізнанні нового, спостережливість, працьовитість; Тип уроку : засвоєння нових знань, умінь, навичок. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП ______________________________________________________ […]...

  23. Знаки тригонометричних функцій Математика – Алгебра Тригонометричні функції Знаки тригонометричних функцій З означення тригонометричних функцій легко зробити висновок щодо знаків тригонометричних функцій у координатних чвертях: Зміна тригонометричних функцій при зростанні “a” від 0 до 2п Зміну , , , при зростанні від 0 до описано в табл. 2. Позначення: – зростає; – спадає....

  24. ПОРІВНЯННЯ СПОСОБІВ УСНОГО ДОДАВАННЯ КРУГЛИХ ТРИЦИФРОВИХ ЧИСЕЛ. ОБЧИСЛЕННЯ ЗНАЧЕНЬ БУКВЕНИХ ВИРАЗІВ. РОЗШИРЕНА ЗАДАЧА НА ЗВЕДЕННЯ ДО ОДИНИЦІ Мета: узагальнити різні способи додавання круглих трицифрових чисел; формувати вміння розв’язувати задачі на зведення до одиниці; повторити обчислення значень виразів зі змінними; розвивати мислення; виховувати уважність. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Перевірка домашнього завдання 2. Гра “Рибалки” (на порівняння чисел) Учні “ловлять” рибу з числами і вкидають у два відерця: […]...

  25. УСНЕ ДОДАВАННЯ ТРИЦИФРОВИХ ЧИСЕЛ ВИДУ 520 + 340. РОЗШИРЕНА ЗАДАЧА НА ЗВЕДЕННЯ ДО ОДИНИЦІ Мета: ознайомити учнів із додаванням трицифрових чисел виду 520 + 340; формувати вміння розв’язувати розширені задачі на зведення до одиниці; вдосконалювати обчислювальні навички; розвивати мислення; виховувати уважність. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Перевірка домашнього завдання 2. Завдання для допитливих (додаток) – У якій країні з’явилися перші школи? Приклади розв’яжіть і […]...

  26. Формули скороченого множення – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Формули скороченого множення (а + b)2 = а2 + 2аb + b2 (квадрат суми); (a – b)2 = а2 – 2ab + b2 (квадрат різниці); A2 – b2 = (a + b)(a – b) (різниця квадратів); (a + b)3 = а3 + 3а2b + 3ab2 + b3 (куб суми); […]...

  27. Визначення структурної формули – Визначення формули АНАЛІЗ ОРГАНІЧНИХ СПОЛУК 1.4 . Визначення структурної формули Для знайденої молекулярної формули спочатку записують усі можливі ізомерні структури. Далі перевіряють типові властивості цих речовин, щоб встановити, яка структурна формула підходить до визначуваної речовини. Приклад. Для молекулярної формули С2Н60 маємо дві можливі структурні формули. Етанол розчиняється у воді (водневий зв’язок), а етер не розчиняється. Етанол на […]...

  28. Знаходження значень виразів на сумісні дії з багатоцифровими числами. Розширені задачі на зведення до одиниці. Складання і розв’язування нерівностей (№№ 1067-1075) Тема. Знаходження значень виразів на сумісні дії з багатоцифровими числами. Розширені задачі на зведення до одиниці. Складання і розв’язування нерівностей (№№ 1067 – 1075). Мета. Виправляти учнів у знаходженні значень виразів на сумісні дії з багатоцифровими числами; удосконалювати вміння розв’язувати задачі на зведення до одиниці; вчити складати і розв’язувати нерівності. Обладнання. Завдання для опитування учнів; […]...

  29. Ділення багатоцифрових чисел на трицифрові у випадку, коли в записі частки є нуль (ознайомлення). Задачі на зведення до одиниці з буквеними даними (№№ 1093-1100) Тема. Ділення багатоцифрових чисел на трицифрові у випадку, коли в записі частки є нуль (ознайомлення). Задачі на зведення до одиниці з буквеними даними (№№ 1093-1100). Мета. Ознайомити учнів із діленням багатоцифрових чисел на трицифрові у випадку, коли в записі частки є нуль; закріплювати вміння учнів розв’язувати задачі на зведення до одиниці. Обладнання. Картки для опитування; […]...

  30. Ділення багатоцифрових чисел на одноцифрові. Ускладнені задачі на зведення до одиниці (№№ 655-662) Тема. Ділення багатоцифрових чисел на одноцифрові. Ускладнені задачі на зведення до одиниці (№№ 655-662). Мета. Закріплювати вміння учнів ділити багатоцифрові числа на одноцифрові; удосконалювати вміння розв’язувати задачі на зведення до одиниці; вправляти у ділені іменованих чисел. Таблиця. Таблиця усних обчислень; картки для опитування. Зміст уроку I. Контроль, корекція та закріплення знань. 1. Перевірка домашнього завдання. […]...

  31. ПОВТОРЕННЯ ТАБЛИЦЬ МНОЖЕННЯ І ДІЛЕННЯ ЧИСЕЛ НА 7. РОЗВ’ЯЗУВАННЯ ЗАДАЧ НА СПОСІБ ЗВЕДЕННЯ ДО ОДИНИЦІ Мета: закріпити навички табличного множення і ділення чисел на 7; формувати вміння використовувати вивчений матеріал під час розв’язування задач і прикладів; вдосконалювати обчислювальні навички, вміння працювати самостійно; виховувати старанність. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Перевірка домашнього завдання – Назвіть значення виразів (с. 31, завдання 205). – Зачитайте відповідь до задачі […]...

  32. Задачі на подвійне зведення до одиниці Мета: формувати уміння розв’язувати задачі на подвійне зведення до одиниці; формувати навички письмового множення на двоцифрове число. Тип уроку: закріплення та застосування знань, умінь та навичок Дидактичні задачі. Вдосконалювати навички усних обчислень (№1; РЗ ч. 1 с. 27, №1). Зіставити задачі на подвійне зведення до одиниці різного рівня складності ( №1); розвивати уміння розв’язувати прямі […]...

  33. НУМЕРАЦІЯ ТРИЦИФРОВИХ ЧИСЕЛ. ТАБЛИЧНЕ МНОЖЕННЯ. ЗАДАЧІ НА ЗВЕДЕННЯ ДО ОДИНИЦІ Мета: ознайомити учнів з підручником математики для 4-го класу; повторити спосіб нумерації чисел у межах 1000; зосередити увагу учнів на значенні цифр у числі залежно від місця в запису числа; повторити зв’язок дій додавання і множення; вдосконалювати вміння розв’язувати задачі на зведення до одиниці; розвивати мислення; виховувати інтерес до предмета. ХІД УРОКУ I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ […]...

  34. Формули радіусів вписаних і описаних кіл правильних многокутників УРОК № 18 Тема. Формули радіусів вписаних і описаних кіл правильних многокутників Мета уроку: Виведення формул для радіусів вписаних і описаних кіл правильного многокутника. Формування вмінь застосовувати виведені формули до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: табл. 5, 6. Вимоги до рівня підготовки учнів: записують і пояснюють формули радіусів вписаного та описаного кіл […]...

  35. УСНЕ ДОДАВАННЯ І ВІДНІМАННЯ КРУГЛИХ ТРИЦИФРОВИХ ЧИСЕЛ БЕЗ ПЕРЕХОДУ ЧЕРЕЗ ДЕСЯТОК. РОЗШИРЕНА ЗАДАЧА НА ЗВЕДЕННЯ ДО ОДИНИЦІ (другий вид) Мета: узагальнити і систематизувати вміння учнів розв’язувати приклади і задачі на вивчені випадки арифметичних дій; ознайомити учнів з другим видом розширених задач на зведення до одиниці; повторити зв’язок між компонентами та результатами арифметичних дій множення і ділення; розвивати мислення; виховувати інтерес до математики. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ (додаток) 1. Перевірка […]...

  36. Тотожності УРОК № 2 Тема. Тотожності sin 2 ? + cos 2 ? = 1; sin (180°- ?) = sin?; cos (180°- ?) = – cos?; sin (90°- ?) = cos?; cos (90°- ?) = sin? Мета уроку: виведення формул sin2? + cos2? = 1; sin(180°- ?) = sin?; cos(180°- ?) = – cos?; sin(90°- ?) […]...

  37. РОЗВ’ЯЗУВАННЯ ЗАДАЧ НА КРАТНЕ ПОРІВНЯННЯ. ВПРАВИ НА ЗАСВОЄННЯ ТАБЛИЦІ МНОЖЕННЯ І ДІЛЕННЯ ЧИСЕЛ НА 7. РОЗШИРЕНА ЗАДАЧА НА ЗВЕДЕННЯ ДО ОДИНИЦІ Мета: вдосконалювати навички розв’язання задач на кратне порівняння, на зведення до одиниці розширеного виду; вдосконалювати знання таблиць множення і ділення, вміння використовувати їх на практиці; розвивати обчислювальні навички, логічне мислення, математичне мовлення, творчі здібності; виховувати уважність. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ (додаток) 1. Перевірка домашнього завдання – Прочитайте розв’язання задачі 232 […]...

  38. РОЗВ’ЯЗУВАННЯ ЗАДАЧ НА СПОСІБ ЗВЕДЕННЯ ДО ОДИНИЦІ (другий вид). РОЗВ’ЯЗУВАННЯ РІВНЯНЬ НА ЗНАХОДЖЕННЯ НЕВІДОМОГО МНОЖНИКА Мета: формувати вміння розв’язувати задачі на спосіб зведення до одиниці; рівняння на знаходження невідомого множника; вдосконалювати знання таблиць множення і ділення, вміння використовувати їх на практиці; розвивати обчислювальні навички; логічне мислення, математичне мовлення; виховувати інтерес до вивчення точних наук. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Перевірка домашнього завдання 2. Усні обчислення […]...

  39. Ділення багатоцифрових чисел на одноцифрові у випадку, коли частка містить всередині нуль. Ускладнені задачі на зведення до одиниці (№№ 672-680) Тема. Ділення багатоцифрових чисел на одноцифрові у випадку, коли частка містить всередині нуль. Ускладнені задачі на зведення до одиниці (№№ 672-680). Мета. Ознайомити учнів із діленням багатоцифрових чисел на одноцифрові у випадку, коли частка містить нуль всередині; закріплювати вміння розв’язувати задачі на зведення до одиниці, складати та обчислювати вирази. Обладнання. Таблиця усних обчислень; гра “Естафета”; […]...

  40. Ділення багатоцифрових чисел на одноцифрові. Перевірка ділення множенням. Ускладнені задачі на зведення до одиниці (№№ 663-671) Тема. Ділення багатоцифрових чисел на одноцифрові. Перевірка ділення множенням. Ускладнені задачі на зведення до одиниці (№№ 663-671). Мета. Закріплювати вміння ділити багатоцифрові числа на одноцифрові; повторити способи перевірки дії ділення; вправляти учнів у розв’язуванні задач на зведення до одиниці. Обладнання. Таблиця усних обчислень; схеми задач; картки для самостійної роботи. Зміст уроку I. Контроль, корекція і […]...

Ви зараз читаєте: Формули зведення
«
»