Головна ⇒ 📌Довідник з математики ⇒ Графіки тригонометричних функцій

Графіки тригонометричних функцій

Математика – Алгебра

Тригонометричні функції

Графіки тригонометричних функцій

Для побудування графіків тригонометричних функцій візьмемо 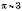Графіки тригонометричних функцій. Побудуємо графік функції 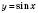Графіки тригонометричних функцій (див. рисунок).
Графіки тригонометричних функцій
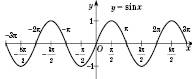
Ця крива називається синусоїдою.
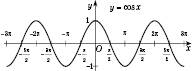
Графік функції 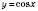Графіки тригонометричних функцій можна дістати з графіка функції 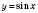Графіки тригонометричних функцій паралельним перенесенням його вліво вздовж осі Ox на 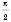Графіки тригонометричних функцій одиниць. Це випливає з формули

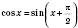Графіки тригонометричних функцій.
Графіки тригонометричних функцій
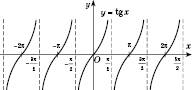
Побудуємо графік функції Графіки тригонометричних функцій:
Графіки тригонометричних функцій
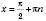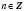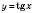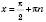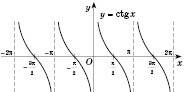
Зверніть увагу: значення Графіки тригонометричних функцій, Графіки тригонометричних функцій, не входять до області визначення функції Графіки тригонометричних функцій. Прямі 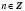Графіки тригонометричних функцій, Графіки тригонометричних функцій, є асимптотами графіка. Графік носить назву Тангенсоїди.
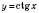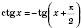Графік функції Графіки тригонометричних функцій легко дістати, скориставшись формулою зведення Графіки тригонометричних функцій:
Графіки тригонометричних функцій
Розглянемо графік
функції
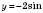
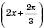Графіки тригонометричних функційГрафіки тригонометричних функцій.
Запишемо функцію у вигляді
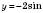
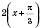Графіки тригонометричних функційГрафіки тригонометричних функцій.
Із цього випливає, що графік цієї функції можемо дістати, якщо побудувати:
1) графік функції Графіки тригонометричних функцій;
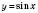2) графік функції 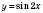Графіки тригонометричних функцій, стискаючи графік функції 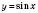Графіки тригонометричних функцій у два рази до оcі Oy;
3) графік функції 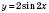Графіки тригонометричних функцій, розтягуючи у два рази вздовж осі Oy графік функції Графіки тригонометричних функцій;
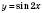4) графік функції 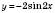Графіки тригонометричних функцій, відображуючи графік функції 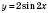Графіки тригонометричних функцій симетрично відносно осі Ox;
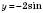
5) графік функції 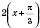Графіки тригонометричних функційГрафіки тригонометричних функцій, паралельно переносячи графік 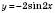Графіки тригонометричних функцій на відстань 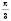Графіки тригонометричних функцій вліво вздовж осі Ox.
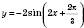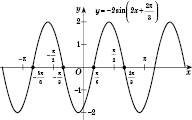
На рисунку не показані поступові перетворення графіка, а тільки остаточний вигляд графіка функції Графіки тригонометричних функцій:
Графіки тригонометричних функцій
Зверніть увагу: на практиці можна відразу побудувати графік функції 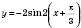Графіки тригонометричних функцій, якщо врахувати такі міркування:
1) графік матиме вигляд синусоїди;
2) точка графіка 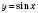Графіки тригонометричних функцій з координатами (0; 0) перейде в шуканому графіку в точку Графіки тригонометричних функцій;
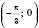3) період функції 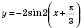Графіки тригонометричних функцій дорівнює Графіки тригонометричних функцій;
4) максимальні й мінімальні значення функції 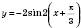Графіки тригонометричних функцій відповідно дорівнюватимуть 2 і –2;
5) синусоїда 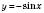Графіки тригонометричних функцій симетрична синусоїді 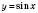Графіки тригонометричних функцій відносно осі Оx.
Таким чином, при зростанні значень аргументу від 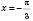Графіки тригонометричних функцій до нескінченності з кроком 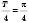Графіки тригонометричних функцій функція набуватиме значення 0; –2; 0; –2; 0… і т. д.
Аналогічно можна міркувати, якщо треба побудувати графіки функцій:
y = Acos(kx+b);
y = Atg(kx+b);
y = Actg(kx+b).
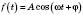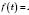
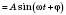Величини, які змінюються за законом Графіки тригонометричних функцій або Графіки тригонометричних функційГрафіки тригонометричних функцій, називаються Гармонічними коливаннями.
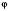При цьому: A – амплітуда коливання; Графіки тригонометричних функцій – циклічна частота коливання; Графіки тригонометричних функцій – початкова фаза коливання.
Період функції 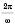Графіки тригонометричних функцій – Період гармонічного коливання.




Related posts:

  1. Перетворення графіків функцій – Функції та графіки Математика – Алгебра Функції та графіки Перетворення графіків функцій 1. Графіки функцій і є симетричними відносно осі Ox. 2. Щоб побудувати графік функції , треба графік функції розтягнути від осі Ox в k разів, якщо , або стиснути його в k разів до осі Ox, якщо . 3. Щоб побудувати графік функції , треба графік […]...
  2. Періодичність тригонометричних функцій Математика – Алгебра Тригонометричні функції Періодичність тригонометричних функцій Функція називається Періодичною з періодом , якщо для будь-якого x з області визначення функції числа і також належать області визначення й виконується умова: . Якщо T – період функції , то всі числа виду nT, де , , також є періодами функції. Щоб побудувати графік періодичної функції […]...
  3. Побудова графіків тригонометричних функцій УРОК 9 Тема. Побудова графіків тригонометричних функцій Мета уроку: побудова графіків функцій у = sin х, у = cos x, у = tg х, у = ctg x. Формування умінь будувати графіки функцій: у = Asin (kx + b), у = Acos (kx + b), у = Atg (kx + b), у = Actg (kx […]...
  4. Властивості функцій – Функції та графіки Математика – Алгебра Функції та графіки Властивості функцій Функція називається Зростаючою на деякому проміжку, якщо більшому значенню аргументу із цього проміжку відповідає більше значення функції. Функція називається Спадною на деякому проміжку, якщо більшому значенню аргументу із цього проміжку відповідає менше значення функції. Якщо функція зростає (спадає) на всій області визначення, її називають зростаючою (спадною). Приклади […]...
  5. Знаки тригонометричних функцій Математика – Алгебра Тригонометричні функції Знаки тригонометричних функцій З означення тригонометричних функцій легко зробити висновок щодо знаків тригонометричних функцій у координатних чвертях: Зміна тригонометричних функцій при зростанні “a” від 0 до 2п Зміну , , , при зростанні від 0 до описано в табл. 2. Позначення: – зростає; – спадає....
  6. Періодичність тригонометричних функцій УРОК 8 Тема. Періодичність тригонометричних функцій Мета уроку: Введення поняття періодичної функції; знаходжен­ня найменших додатних періодів тригонометричних функцій; формування умінь знаходити періоди функцій У = sin (kx + b), у = cos (kx + b), У = tg (kx + b), у = ctg (kx + b). І. Перевірка домашнього завдання 1. Побудуйте на одиничному […]...
  7. Властивості тригонометричних функцій УРОК 10 Тема. Властивості тригонометричних функцій Мета уроку: вивчення властивостей тригонометричних функцій у = sin х, у = cos х, у = tg х, у = ctg x (область визначення; область значень; парність (непарність); симетричність графіків; періодичність; нулі; проміжки спадання (зростання); проміжки знакопостійності; найбільші і найменші значення). І. Перевірка домашнього завдання Перевірити правильність побудови графіків […]...
  8. Властивості тригонометричних функцій – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Властивості тригонометричних функцій Функції У = sin x У = cos x Y = tg x 1. Область визначення Х (-∞;+∞) Х (-∞;+∞) X ≠ π/2 + πn, n Z 2. Множина значень Y Y Y (-∞;+∞) 3. Періодичність Усі тригонометричні функції – періодичні з найменшим додатним періодом Т […]...
  9. Приклади функцій і їх графіків Математика – Алгебра Функції Приклади функцій і їх графіків Лінійна функція Лінійною називається функція, яку можна задати формулою , де х – аргумент, а k і b – дані числа. Графік лінійної функції – пряма. k називається Кутовим коефіцієнтом прямої, яка є графіком лінійної функції. Кожна пряма на координатній площині, яка не є перпендикулярною до […]...
  10. Найпростіші перетворення графіків функцій УРОК № 21 Тема. Найпростіші перетворення графіків функцій Мета уроку: закріпити знання учнів про види геометричних перетворень графіків функцій і зв’язок між видом перетворення та видом рівняння, що задає дану функцію. Закріпити схеми міркувань, що передують побудові графіка деякої функції шляхом геометричних перетворень графіка однієї з елементарних функцій. Закріпити вміння виконувати послідовні перетворення графіків елементарних […]...
  11. Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і по­ловинного аргументу УРОК 13 Тема. Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і по­ловинного аргументу Мета уроку: вивчення формул тригонометричних функцій суми і різниці двох чисел, формул тригонометричних функцій подвійного і половинного аргументу. Фор­мування умінь застосовувати вивчені формули для спрощення виразів та обчислень. І. Перевірка домашнього завдання Розв’язання вправ, аналогічних до домашніх: вправа […]...
  12. Розв’язування вправ. Самостійна робота УРОК 4 Тема. Розв’язування вправ. Самостійна робота Мета уроку: формування умінь будувати графіки функцій за до­помогою геометричних перетворень. І. Перевірка домашнього завдання 1. Один учень відтворює розв’язування вправи № 3 (4; 5; 6), дру­гий – № 3 (7; 8; 9), третій – № 3 (18). 2. Математичний диктант. Запишіть формулою функцію, графік якої одержано в […]...
  13. Побудова графіків функцій за допомогою геомет­ричних перетворень відомих графіків функцій УРОК 3 Тема. Побудова графіків функцій за допомогою геомет­ричних перетворень відомих графіків функцій Мета уроку: Формування умінь будувати графіки функцій за до­помогою восьми базових перетворень графіка функції У = f(x): у = – f(x); у = f(-x); у = f(x) + b; у = f(x + a); у = af(x); у = f(ax); у = […]...
  14. Повторення та систематизація знань та вмінь учнів з теми “Функції і графіки” Урок № 85 Тема. Повторення та систематизація знань та вмінь учнів з теми “Функції і графіки” Мета: повторити та систематизувати набуті учнями знання про зміст основних понять теми та види задач; повторити та систематизувати основні способи дій, що були опановані учнями під час вивчення теми; провести підготовку до підсумкового тематичного оцінювання. Тип уроку: повторення та […]...
  15. Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60° Урок № 57 Тема. Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60° Мета: сформувати в учнів свідоме розуміння змісту та доведення теореми, що містить формули доповнення, а також наслідку з неї; домогтися засвоєння учнями способу обчислення та значень тригонометричних функцій кутів 30°, 45° і 60°. Закріпити знання вивчених формул та сформувати вміння їх застосовувати […]...
  16. Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60°. Розв’язування задач Урок № 58 Тема. Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60°. Розв’язування задач Мета: закріпити знання учнями змісту формул доповнення та числових значень тригонометричних функцій кутів 30°, 45°, 60°. Сформувати вміння застосовувати формули до розв’язування задач. Тип уроку: застосування знань, умінь та навичок. Наочність та обладнання: конспект 22. Хід уроку I. Організаційний етап […]...
  17. Функції та графіки. Лінійна функція Урок № 67 Тема. Функції та графіки. Лінійна функція Мета: повторити та узагальнити відомості щодо змісту основних понять теми; повторити, систематизувати набуті практичні вміння; провести підготовку до тематичної контрольної роботи. Тип уроку: узагальнення та систематизація знань, умінь, навичок. Хід уроку I. Організаційний момент 1. Готовність до уроку. 2. План роботи на уроці. II. Перевірка домашнього […]...
  18. Квадратична функція – Функції та графіки Математика – Алгебра Функції та графіки Квадратична функція Квадратним тричленом називається многочлен виду , де x – змінна, a, b і c – деякі числа, причому . Коренем квадратного тричлена називається таке значення змінної, яке перетворює квадратний тричлен на 0. Щоб знайти корені квадратного тричлена, треба розв’язати квадратне рівняння . Теорема. Якщо і – корені […]...
  19. Огляд властивостей основних функцій УРОК 2 Тема. Огляд властивостей основних функцій Мета уроку: Повторення і узагальнення властивостей елементарних функцій: у = kx + b, у = , у = х2, у= х3, у = , у = , у = ?х2 + bx + с. І. Перевірка домашнього завдання 1. Один учень пояснює розв’язання вправи № 1 (5), другий […]...
  20. РІВНЯННЯ РУХУ. ГРАФІКИ РІВНОМІРНОГО ПРЯМОЛІНІЙНОГО РУХУ Роздiл 2 МЕХАНІЧНИЙ РУХ &18. РІВНЯННЯ РУХУ. ГРАФІКИ РІВНОМІРНОГО ПРЯМОЛІНІЙНОГО РУХУ Рівномірний прямолінійний рух тіла дуже зручно представляти і вивчати у вигляді графіків залежності шляху, пройденого тілом, від часу його руху (графік руху) і залежності швидкості тіла від часу його руху (графік швидкості). Розглянемо приклад. Нехай автомобіль рухається з Києва до Одеси зі швидкістю 100 […]...
  21. Основні властивості неперервних функцій Математика – Алгебра Границя Основні властивості неперервних функцій Теорема 1. Якщо функції і є неперервними в точці , то в цій точці будуть неперервними і функції , . Теорема 2. Якщо і є неперервними в точці і , то в точці є неперервною також і функція . Зверніть увагу: всі дробово-раціональні функції і основні тригонометричні […]...
  22. Графіки залежності кінематичних величин від часу в разі рівномірного прямолінійного руху 1-й семестр МЕХАНІКА 1. Кінематика Урок 5/7 Тема. Графіки залежності кінематичних величин від часу в разі рівномірного прямолінійного руху Мета уроку: ознайомити учнів з графічною інтерпретацією рівномірного прямолінійного руху Тип уроку: вивчення нового матеріалу План уроку Контроль знань 5 хв. 1. Прямолінійний рівномірний рух. 2. Відносність механічного руху. 3. Закон додавання швидкостей. 4. Правило додавання […]...
  23. ГРАФІКИ ШЛЯХУ І ШВИДКОСТІ Розділ ІІ Механічний рух & 14. ГРАФІКИ ШЛЯХУ І ШВИДКОСТІ Визначення шляху на графіку швидкості У фізиці й математиці використовують три способи подання інформації про зв’язок між різними величинами: а) у вигляді формули, наприклад, s =v ∙ t; б) у вигляді таблиці; в) у вигляді графіка (малюнка). Залежність швидкості від часу v(t) – графік швидкості, […]...
  24. Рівняння руху. Графіки рівномірного прямолінійного руху МЕХАНІКА РОЗДІЛ 2. МЕХАНІЧНИЙ РУХ § 18. Рівняння руху. Графіки рівномірного прямолінійного руху Запитання до вивченого 1. Для того щоб побудувати графік залежності пройденого автомобілем шляху від часу руху, потрібно скористатися формулою l = vt і скласти таку відповідну таблицю. Час t, год Шлях l, км 0 0 1 100 2 200 3 300 Далі […]...
  25. Практична робота 3. Використання формул і вбудованих функцій у середовищі табличного процесора. Використання логічних функцій для опрацювання табличної інформації ТЕМА 5.4. ЕЛЕКТРОННІ ТАБЛИЦІ (10 ГОДИН) Урок 54 Практична робота 3. Використання формул і вбудованих функцій у середовищі табличного процесора. Використання логічних функцій для опрацювання табличної інформації Мета: – формувати теоретичну базу знань учнів з теми, спираючись на міжпредметні зв’язки; – розвивати практичні вміння та навички щодо опрацювання табличної інформації за допомогою формул та вбудованих […]...
  26. Основні теореми про границі функцій Математика – Алгебра Границя Основні теореми про границі функцій Теорема 1. Якщо функції і в точці мають границі, то сума і добуток цих функцій також мають у цій точці границю, причому ; . Теорема 2. Якщо функції і в точці мають границі й , то й функція має в цій точці границю, яка дорівнює . […]...
  27. ГРАФІКИ РІВНОМІРНОГО РУХУ Розділ 2 МЕХАНІЧНИЙ РУХ & 10. ГРАФІКИ РІВНОМІРНОГО РУХУ Спортсмен, велосипед якого має спідометр, рухається по трасі (рис. 10.1). Швидкість руху, яку показує спідометр у будь-який момент часу, дорівнює 5 м/с. Як описати рух цього спортсмена і взагалі будь-якого тіла за допомогою графіків? Згадаємо, адже графіки руху тіл ви вивчали в курсі математики 6 класу. […]...
  28. Розділ 4. Функції Або немає розв’язку. 6. 1) Так; 2) ні; 3) ні; 4) так. 7. 1) -4 = -2 • (-1)2 – 3 + 1; -4 = -2 – 3 + 1; -4 = -4; А належить графіку функції; 2) 0 ≠ -2 • 12 + 3 + 1; 0 ≠ -2 + 4; 0 ≠ 2; […]...
  29. ГРАФІКИ ЗАЛЕЖНОСТЕЙ МІЖ ВЕЛИЧИНАМИ Розділ 5 ВИРАЗИ І РІВНЯННЯ § 35. ГРАФІКИ ЗАЛЕЖНОСТЕЙ МІЖ ВЕЛИЧИНАМИ Ви знаєте, що вартість товару залежить від його кількості: що більшу кількість товару купують, то більшою буде його вартість. Наприклад, якщо ціна одного кілограма цукерок становить 35 грн, то за 2 кг треба заплатити 70 грн, за 3 кг – 105 грн тощо. Ви […]...
  30. РЕГУЛЯЦІЯ ФУНКЦІЙ В ОРГАНІЗМІ – НЕЙРОГУМОРАЛЬНА РЕГУЛЯЦІЯ ФІЗІОЛОГІЧНИХ ФУНКЦІЙ – ЛЮДИНА Біологія – універсальний довідник ЛЮДИНА НЕЙРОГУМОРАЛЬНА РЕГУЛЯЦІЯ ФІЗІОЛОГІЧНИХ ФУНКЦІЙ РЕГУЛЯЦІЯ ФУНКЦІЙ В ОРГАНІЗМІ Для регуляції фізіологічних процесів відповідно до потреб організму і змін навколишнього середовища існує два механізми: гуморальний і нервовий. Гуморальна регуляція фізіологічних процесів здійснюється за допомогою хімічних речовин, які поступають із різних органів і тканин тіла у кров і розносяться нею по всьому […]...
Ви зараз читаєте: Графіки тригонометричних функцій
«
»