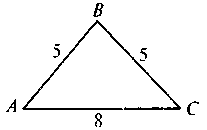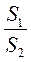Метод площ. Розв’язування задач
Урок № 51
Тема. Метод площ. Розв’язування задач
Мета: закріпити, систематизувати та узагальнити знання учнів з теми “Площі многокутників”. Сформувати в учнів розуміння схеми дій, що відповідають змісту поняття “метод площ”. Провести діагностику рівня засвоєння учнями навчального матеріалу розділу ІІІ.
Тип уроку: комбінований.
Наочність та обладнання: конспекти і 7-20.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Розв’язання задач перевіряються під час коментування за готовими
Математичний диктант
Варіант 1 | Варіант 2 | |
1 | Гіпотенузи двох подібних прямокутних трикутників відносяться як 3 : 2. Яке відношення площ цих трикутників? | Площі подібних рівносторонніх трикутників відносяться як 4 : 25. Яке відношення довжин сторін цих трикутників? |
2 | Відношення площ двох трикутників із кутами 40° і 50° дорівнює 16. Чому дорівнює відношення їх периметрів? | Відношення |
3 | Як зміниться площа трикутника, якщо всі його медіани зменшити у 2 рази? | Як зміниться площа трикутника, якщо всі його висоти збільшити у 3 рази? |
III. Формулювання мети і завдань уроку
Учитель повідомляє учням, що вивчення поняття площі многокутника, її властивостей та формул для обчислення площ вивчених видів чотирикутників, трикутників, крім суто практичного спрямування, має ще й методологічне значення, тобто дає на озброєння учням ще один метод розв’язування задач (і не тільки задач, в яких мова йде про обчислення площ). Отже, мета уроку – вивчення схеми дій, передбаченої змістом поняття “метод площ”, а також формування вмінь застосовувати цю схему під час розв’язування задач.
IV. Актуалізація опорних знань
Оскільки матеріал уроку грунтується на застосуванні вивчених раніше формул площ у новій ситуації відповідно до схеми, описаної в коментарі до методу площ, то учням слід повторити формули площ, їх наслідки та способи застосування в стандартних ситуаціях.
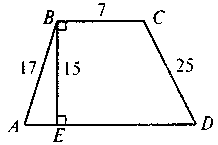
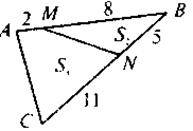
Виконання письмових вправ за готовими рисунками
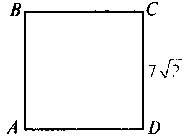
1 |
| ?BCD – квадрат. Знайдіть SАВCD |
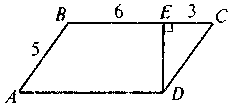
2 |
| ABCD – паралелограм. Знайдіть SАВСD |
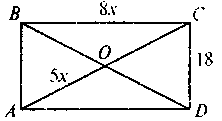
3 |
| ABCD – прямокутник. Знайдіть SАВСD |
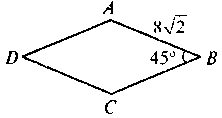
4 |
| ABCD – ромб. Знайдіть SАВСD |
5 |
| Знайдіть S? АВС. |
6 |
| Знайдіть SАВСD |
7 |
| Знайдіть відношення |
8 |
| ABCD – трапеція. Знайдіть SАВСD |
V. Засвоєння знань
@ Зміст навчального матеріалу уроку є корисним доповненням, зробленим авторами нового підручника до традиційного змісту матеріалу, що вивчався в темі “Плоті”, і є узагальненням тих способів дій, які, можливо, виконували учні, вивчаючи цю тему в попередні роки. До вивчення на уроці пропонується розгляд способів розв’язання деяких задач, що пов’язані із застосуванням обчислення площ за вивченими у класі формулами. Вивчення матеріалу на уроці проводиться за підручником (як варіант – запропонувати спочатку розв’язати задачі самостійно, а після виконання звернутися до підручника), причому необхідно не просто ознайомитися зі змістом розв’язання, а й провести роботу з його усвідомлення (цю роботу можна провести у формі бесіди) Результат цієї роботи повинен мати вигляд певної схеми дій, що містить ознаки, за якими можна визначити серед інших задачу, в якій можливо застосувати метод площ, а також приблизний опис дій під час розв’язування задач цим методом.
VI. Формування первинних умінь
Виконання письмових вправ
1. Дві сторони трикутника дорівнюють 12 см і 18 см. Знайдіть висоту, проведену до меншої з них, якщо висота, проведена до більшої сторони, дорівнює 4 см.
2. Користуючись методом площ, доведіть, що в рівнобедреному трикутнику висоти, проведені до бічних сторін, рівні.
3. Периметр паралелограма дорівнює 56 см. Знайдіть сторони паралелограма, якщо його висоти дорівнюють 6 см і 8 см.
4. Діагоналі ромба дорівнюють 30 см і 40 см. Користуючись методом площ, знайдіть висоту ромба.
5. Доведіть методом площ, що паралелограм із рівними висотами є ромбом.
6*. Пряма, паралельна стороні трикутника, ділить його на дві рівновеликі частини. У якому відношенні ця пряма ділить дві інші сторони трикутника?
7. Доведіть, що сторони трикутника обернено пропорційні його висотам: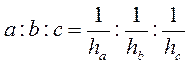 
.
VII. Домашнє завдання
Повторити теоретичний матеріал з теми “Площі многокутників”.
Виконати тестове завдання.
1. Назвіть формулу площі трапеції з основами а і b та висотою А.
А)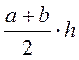 
; б) 
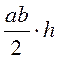; в) (a + b)h; г) 
.
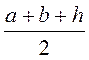2. Назвіть формулу площі ромба з діагоналями d1 та d2.
а)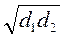 
; б) 
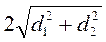; в)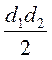 
; г) d1d2.
3. Площа трикутника ABC дорівнює S. Знайдіть площу трикутника, який відтинає від трикутника ABC середня лінія.
A)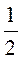 
S; б) 
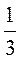S; в)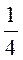 
S; г) визначити неможливо.
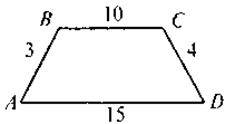
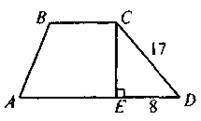
4. За даними рисунка знайдіть площу трапеції A BCD, якщо її середня лінія дорівнює 10.
А) 120; б) 300; в) 150; г) 136.
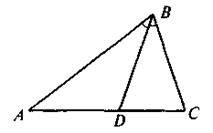
5. Відрізок BD – бісектриса трикутника ABC (рисунок). Площі трикутників BDC і ABC відносяться як 4 : 9. Знайдіть відношення АВ. ВС.
А) 5: 2; б) 4 : 5; в) 3 : 2; г) 5 : 4.
Розв’язати задачі.
1. Висоти паралелограма дорівнюють 6 см і 4 см, а менша сторона – 8 см. Знайдіть периметр паралелограма.
2. Доведіть методом площ, то трикутник із рівними висотами є рівностороннім.
3. Доведіть методом площ метричне співвідношення у прямокутному трикутнику: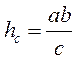 
.
4. Сума відстаней від точки основи рівнобедреного трикутника до його бічних сторін не залежить від вибору точки. Доведіть.
(1 votes, average: 5.00 out of 5)
Loading...