Головна ⇒ 📌ГДЗ з математики ⇒ Рівні трикутники. Висота, медіана, бісектриса трикутника

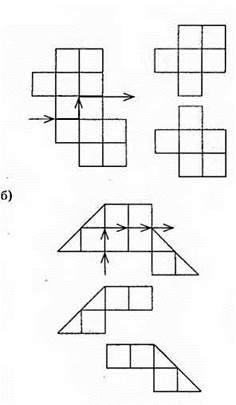
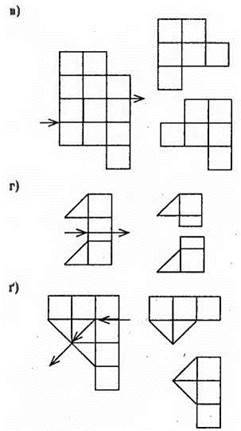
Рівні трикутники. Висота, медіана, бісектриса трикутника

§ 2. Трикутники

6. Рівні трикутники. Висота, медіана, бісектриса трикутника

Практичні завдання

132.

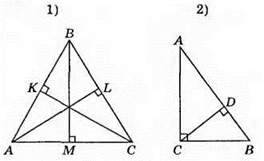
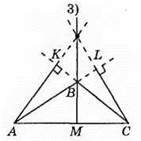
Рівні трикутники. Висота, медіана, бісектриса трикутника Рівні трикутники. Висота, медіана, бісектриса трикутника

133. ВН – спільна висота трикутників ABD, ABC, BDC. ВН лежить поза трикутником BCD.

Рівні трикутники. Висота, медіана, бісектриса трикутника

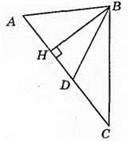
134.

Рівні трикутники. Висота, медіана, бісектриса трикутника

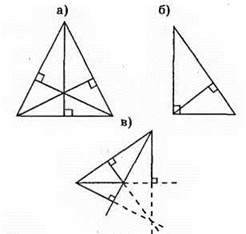
135.

Рівні трикутники. Висота, медіана, бісектриса трикутника

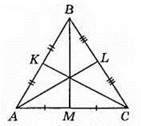
136.

Рівні трикутники. Висота, медіана, бісектриса трикутника

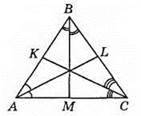
Вправи

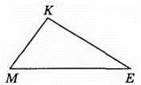
137. 1) ME; 2) ∠E; 3) MK i KE; 4) ∠K i ∠E.

Рівні трикутники. Висота, медіана, бісектриса трикутника

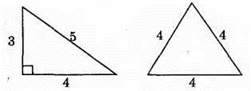
138. 1) ∠E; 2) ∠C i ∠E;3) CF; 4) CF і EF.

139. Нехай довжина першої сторони – х см, другої – 5х

см, а третьої – х + 25 см. За умовою задачі х + 5х + х + 25 = 74, тоді 7х + 25 – 74, 7х = 74 – 25; 7х = 49; х = 49: 7; х = 7. Отже, сторони трикутника дорівнюють 7 см, 35 см, 32 см.

Відповідь: 7 см, 35 см, 32 см.

140. Нехай сторони трикутника дорівнюють 5х см, 7х см, 11х см. За умовою задачі маємо: 11х + 5х = 80, звідси 16х = 80; х = 80 : 16; х = 5. Тоді сторони трикутника дорівнюють 5 x 5 = 25(см), 7 x 5 = 35 (см), 11 x 5 = 55 (см), а його периметр дорівнює 25 см + 35 см + 55 см = 115 см.

Відповідь: 25 см, 35 см, 55 см, 115 см.

141. Нехай сторони трикутника дорівнюють 7х см, 9х см, 8х см. За умовою задачі маємо: 7х + 9х + 8х = 48, звідси 24х = 48; х = 48 : 24; х = 2. Тоді сторони трикутника дорівнюють 7 x 2 = 14(см), 9 x 2 = 18 (см),

8 x 2 = 16 (см).

Відповідь: 14 см, 18 см, 16 см.

142. Оскільки МE = РK, то МЕ = 10 см.

143. Оскільки ∠D = ∠B, то ∠D = 32°.

144. Оскільки ∠T = ∠C, то ∠T = 40°. Оскільки AB = МК, то AB = 5 см.

145. 1) Якщо трикутники рівні, то їх периметри рівні – правильне твердження.

2) Якщо периметри двох трикутників рівні, то й самі трикутники рівні – хибне твердження.

Рівні трикутники. Висота, медіана, бісектриса трикутника

146. Трикутнику належать бісектриси і медіани.

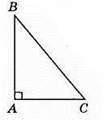
147. Зі стороною трикутника може співпадати висота, де можливо для прямокутного трикутника. AB і АС – висоти трикутника ABC.

Рівні трикутники. Висота, медіана, бісектриса трикутника

148. 1) У тупокутному трикутнику одна висота може належати трикутнику, ВН – висота.

Рівні трикутники. Висота, медіана, бісектриса трикутника

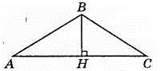
2) Не може тільки одна висота збігатися зі стороною трикутника.

3) У прямокутному трикутнику три висоти перетинаються у вершині прямого кута.

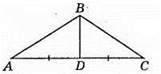
149. Нехай AB + BD +AD = 32 см, ВС + BD + DC = 36 см, BD – медіана і BD = 10 см.

Оскільки AB + BD + AD = 32 см і BD = 10 см, то АB + 10 + AD = 32, звідси AB + AD = 22. Оскільки ВС + BD + DC = 36 см і BD = 10 см, то ВС + DC + 10 = 36, звідси ВС + DC = 26. Тоді Р? ABC =AB + ВС + АС = AB + ВС + (AD + DC) =(AB +AD) + (ВС + DC) = 22 + 26 = 48 (см).

Рівні трикутники. Висота, медіана, бісектриса трикутника

Відповідь: 48 см.

150. Нехай Р? ABC = 60 см, Р? ABD = 36 см, Р? BCD = 50 см.

Р? ABD + Р? BCD = 36 + 50 + 86. З іншого боку Р? ABD + Р? BCD = АВ + AD + BD + ВС + CD + BD = AB + ВС + 2BD + (AD + DC) = AB + ВС + АС + 2BD = Р? ABC + 2 BD. Отже, Р? ABC + 2BD = 86, тоді 60 + 2BD = 86, звідси 2BD = 86 – 60; 2BD = 26; BD = 26 : 2; BD = 13. Таким чином, BD = 13 см.

Відповідь: 13 см.

Вправи для повторення

151. КЕ = PF = ЕТ = 2 см, KF = РТ = 3 см.

152. Нехай ∠CBD = x°, тоді ∠ABD = 5х° і за умовою задачі маємо 5х + х = 72, звідси 6х = 72; х = 72 : 6; х = 12. Отже, ∠CBD = 12°, ∠ABD = 5 x 12° = 60°. Оскільки промінь ВА є бісектрисою кута DBK, то ∠ABK = 60° і тоді ∠DBK = 60° х 2 = 120° – тупий кут.

Рівні трикутники. Висота, медіана, бісектриса трикутника

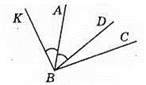
Відповідь: ∠DBK = 120° – тупий.

Спостерігайте, рисуйте, конструюйте, фантазуйте

153.

Рівні трикутники. Висота, медіана, бісектриса трикутника

Рівні трикутники. Висота, медіана, бісектриса трикутника


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника Розділ 3. Трикутники. Ознаки рівності трикутників § 15. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника 351. 1) AT – висота трикутника ABC. 2) AN – медіана трикутника ABC. 3) АР – бісектриса трикутника? AВС. 352. Оскільки AK – висота, то ∠BKA = ∠CKA = 90°. 353. Оскільки АК – бісектриса, то ∠BAK = […]...

  2. Висота, бісектриса, медіана трикутника Геометрія Основні властивості найпростіших геометричних фігур Висота, бісектриса, медіана трикутника Висотою Трикутника, опущеною з да­ної вершини, називається перпендикуляр, проведений із цієї вершини до прямої, що містить протилежну сторону трикутника. У кожному трикутнику можна провести три висоти. Висоти трикутника (або прямі, що їх містять) перетинаються в одній точці. На рисунках зображено, як перетинаються висоти в гострокутному […]...

  3. Медіана, бісектриса і висота трикутника Урок № 24 Тема. Медіана, бісектриса і висота трикутника Мета: домогтися засвоєння учнями: – змісту понять “медіана трикутника”; “бісектриса трикутника”; “висота трикутника”; – уявлення про положення висот у різних видах трикутника. Сформувати вміння: – зображати медіани, висоти та бісектриси трикутника; – розрізняти ці відрізки, виходячи з умови задачі. Тип уроку: застосування знань, умінь та навичок. […]...

  4. Ознаки рівнобедреного трикутника § 2. Трикутники 9. Ознаки рівнобедреного трикутника 232. ?ABC – рівнобедрений, тому ВК є бісектрисою кута ABC, отже, ∠ABC = 2 х ∠ABK = 2 x 25° = 50°. Відповідь: 50°. 233. BK є висотою та медіаною, тому? ABC – рівнобедрений, AB = ВС, отже, ∠C = ∠A =17°. Відповідь: 17°. 234. AС = ВС, […]...

  5. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...

  6. Зовнішній кут трикутника та його властивості Розділ 3. Трикутники. Ознаки рівності трикутників § 18. Зовнішній кут трикутника та його властивості 438. ∠BAK – зовнішній кут при вершині А. 439. ∠LDP – зовнішній кут при вершині D. 441. ∠A + ∠B = 70° – за властивістю зовнішнього кута трикутника. 442. Зовнішній кут трикутника при вершині С дорівнює 74° згідно з властивістю зовнішнього […]...

  7. Сума кутів трикутника. Нерівність трикутника § 3. Паралельні прямі. Сума кутів трикутника § 15. Сума кутів трикутника. Нерівність трикутника Вправи 357. Нехай х° – третій кут трикутника, тоді 35 + 96 + х = 180, звідси х + 131 = 180; х = 180 – 131; х = 49. Отже, третій кут дорівнює 49°. Відповідь: 49°. 358. Нехай х° – […]...

  8. Описане та вписане коло трикутника § 3. Паралельні прямі. Сума кутів трикутника § 20. Описане та вписане коло трикутника 540. 1) Різносторонній гострокутний трикутник. 2) Прямокутний трикутник. 3) Тупокутний трикутник. 541. 1) Рівнобедрений гострокутний трикутник. 2) Рівнобедрений тупокутний трикутник. 542. 543. 544. Вправи 545. Медіана BD рівнобедреного трикутника ABC є в той же час і серединним перпендикуляром до сторони АС […]...

  9. Властивості кутів трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 10. Властивості кутів трикутника 344. ∠E = 60°, ∠F = 40°, ∠D = 80°. ∠E + ∠F + ∠D = 60° + 40° + 80° = 180°. 345. На мал. 208 неправильно сказано градусну міру кутів? АВС, оскільки? ABC – прямокутний, a ∠B + ∠C = […]...

  10. Кут. Вимірювання кутів. Бісектриса кута Розділ 1. Елементарні геометричні фігури та їхні властивості § 3. Кут. Вимірювання кутів. Бісектриса кута 33. 1) М – вершина кута, МА і МК – сторони кута АМК; 2) L – вершина кута, LP і LF – сторони кута PLF; 3) N – вершина кута, NB i NC – сторони кута BNC. 34. 1) O […]...

  11. Властивості й ознака рівнобедреного трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 12. Властивості й ознака рівнобедреного трикутника 476. На мал. 72: ML і МК – бічні сторони, KL – основа, ∠K = ∠L. 477. KD = DF, КЕ = EF, ∠K = ∠F, ∠KDE = ∠FDE, ∠DEK = ∠DEF = 90°. 478. Щоб провести бісектрису, медіану і […]...

  12. Площа трикутника Геометрія Площі фігур Площа трикутника , де h – висота, a – сторона, до якої проведена ця висота. Оскільки , то . Висоти трикутника обернено пропорційні сторонам, на які вони опущені. Зверніть увагу: більшій стороні трикутника відповідає менша висота, і навпаки. , , де P – периметр трикутника, r – радіус вписаного кола. , , […]...

  13. Властивості прямокутного трикутника § 3. Паралельні прямі. Сума кутів трикутника § 17. Властивості прямокутного трикутника 457. Найбільший катет трикутника дорівнює 24 см. 458. ?DEF – прямокутний, ∠F = 90°, ∠D = 30°, DE = 18 см. Відповідь: 9 см. 459. ?KCM – прямокутний, ∠M = 90°, ∠C = 60°, MC = 7 см. ∠MKC = 90° – 60° […]...

  14. Знаходження площі трикутника за двома сторонами і кутом між ними УРОК № 12 Тема. Знаходження площі трикутника за двома сторонами і кутом між ними Мета уроку: виведення формули для знаходження площі трикутника за двома сторонами і кутом між ними. Формування вмінь застосовувати виведену формулу до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника”[13]. Вимоги до рівня підготовки учнів: […]...

  15. Рівнобедрений трикутник і його властивості § 2. Трикутники 8. Рівнобедрений трикутник і його властивості Практичні завдання 196. 197. 198. Вправи 199. 1) Р = 13 + 2 х 8 = 29(см). Відповідь: 29 см. 2) Нехай х см – бічна сторона, тоді 15 + 2х = 39, тоді 2х = 39 – 15; 2х = 24; х = 24 : […]...

  16. Знаходження площі трикутника за радіусом вписаного та описаного кіл УРОК № 14 Тема. Знаходження площі трикутника за радіусом вписаного та описаного кіл Мета уроку: виведення формул для знаходження площі трикутника за радіусом вписаного та описаного кіл. Формування вмінь учнів застосовувати виведені формули до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Площі трикутників і чотирикутників” [13], посібник [14]. Вимоги до рівня підготовки учнів: […]...

  17. Взаємне розміщення двох кіл Розділ 4. Коло і круг. Геометричні побудови § 25. Взаємне розміщення двох кіл 656. На рис. 404 кола перетинаються. На рис. 405 кола дотикаються. На рис. 406 кола не мають спільних точок. 657. 1) Кола мають внутрішній дотик. 2) Кола перетинаються. 3) Кола концентричні. 658. 1) Кола мають зовнішній дотик. 2) Кола не перетинаються. 659. […]...

  18. Властивості конуса 1. 1) Твірна конуса не може утворювати з його основою прямий кут, оскільки Вона є гіпотенузою трикутника обертання, яка утворює бічну поверхню конуса. 2) Теж не може (обгрунтування у п. 1). Якщо конус зрізаний 1) ні; 2) так. Відповідь: 1) ні; 2) ні для зрізаного конуса 1) ні, 2) так. 2. Нехай SA – твірна […]...

  19. Суміжні та вертикальні кути § 1. Найпростіші геометричні фігури та їхні властивості § 4. Суміжні та вертикальні кути Практичні завдання 86. ∠BAC – гострий, ∠OAB – суміжний до кута ВАС. ∠АОВ – прямий, ∠COA – суміжний до кута АОВ. ∠BOC – тупий, ∠AOB – суміжний до кута ВОС. 87. ∠AOC і ∠COB – суміжні. 88. а) ∠ABD i ∠CBD; […]...

  20. Рівносторонній трикутник – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Рівносторонній трикутник Усі висоти, медіани й бісектриси мають однакову довжину. Вписане і описане коло мають спільний центр. Середня лінія трикутника – відрізок, що сполучає середини двох сторін трикутника. Теорема: Зовнішній кут трикутника – кут, суміжний із внутрішнім кутом трикутника. Теорема: Теорема косинусів: у будь-якому трикутнику зі сторонами а, b, с […]...

  21. Теореми про рівність і подібність трикутників – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Трикутник – де багатокутник із трьома сторонами. Сторони трикутника позначаються малими буквами, що відповідають позначенню протилежних вершин. Якщо всі три кути гострі – трикутник гострокутний. Якщо один з кутів прямий – прямокутний; сторони, що утворюють прямий кут, називаються катетами (а і b), сторона проти прямого кута – гіпотенузою (с). Якщо […]...

  22. Трикутник і його елементи Розділ 1. Найпростіші геометричні фігури та їх властивості § 9. Трикутник і його елементи 292. На мал. 194 зображені трикутники ABD, ABC, ОВС. Проти кута C в трикутнику АВС лежить сторона АB, в трикутнику DBC – сторона BD. Прилеглими до кута С в трикутнику ABC є сторони АС і ВС, в трикутнику DBC – сторони […]...

  23. НЕРІВНОСТІ ТРИКУТНИКА РОЗДІЛ 3 ТРИКУТНИКИ & 15. НЕРІВНОСТІ ТРИКУТНИКА Ви вже знаєте, що кожна сторона трикутника менша від суми двох інших його сторін. Щоб довести це твердження як теорему, спочатку розглянемо іншу теорему. Теорема 19 У кожному трикутнику проти більшої сторони лежить більший кут, а проти більшого кута – більша сторона. Доведення. 1) Нехай у трикутнику ABC […]...

  24. СУМА КУТІВ ТРИКУТНИКА РОЗДІЛ 3 ТРИКУТНИКИ & 10. СУМА КУТІВ ТРИКУТНИКА Теорема 8 Сума кутів трикутника дорівняй: 180°. Доведення. Нехай ABC – довільний трикутник (мал. 130). Через йот вершину С проведемо пряму КР, паралельну стороні АВ. Утворені кути АСК і ВСР позначимо цифрами 1 і 2. Тоді ∠A = ∠1, ∠B = ∠2, як внутрішні різносторонні кути при […]...

  25. Ознаки рівності прямокутних трикутників Розділ 1. Найпростіші геометричні фігури та їх властивості § 14. Ознаки рівності прямокутних трикутників 549. Ні, трикутники не рівні. 550. Мал. 319. ?САВ = ?HDQ (за катетом і гострим кутом: CA = HD, ∠C = ∠H). Мал. 320. ?ABC = ?CDA (за гіпотенузою АС і гострим кутом: ∠BAC = ∠DAC). Мал. 321. ?АОВ = ?DCО […]...

  26. Відрізок. Вимірювання відрізків. Відстань між двома точками Розділ 1. Елементарні геометричні фігури та їхні властивості § 2. Відрізок. Вимірювання відрізків. Відстань між двома точками 13. На рисунку зображені відрізки: AB, AK, BK, ВМ. AK = 38 мм, MB = 12 мм. 14. На рисунку зображені відрізки: PC, PD, CD, PT. PC = 9 мм. PD = 31 MM. PT = 27 мм. […]...

  27. Кути трикутника і чотирикутника. Розв’язання задач Урок № 51 Тема. Кути трикутника і чотирикутника. Розв’язання задач Мета. Продовжити формування в учнів. вміння розв’язувати задачі геометричного змісту, повторити основні поняття теми, сприяти формуванню практичних навичок при виконанні вправ. Форми роботи: фронтальна бесіда, індивідуальна робота біля дошки, виконання тренувальних вправ, робота з підручником. Обладнання: лінійка, транспортир, кольорова крейда, косинець, таблиці. Тип уроку: урок […]...

  28. Кути трикутника і чотирикутника Урок № 50 Тема: Кути трикутника і чотирикутника Мета. Познайомити учнів з видами кутів і трикутників в залежності від кутів, які входять до кута. Навчити учнів вимірювати кути за допомогою транспортира. Формувати уміння і навички розв’язувати геометричні задачі. Розвивати логічне мислення учнів, шляхом розв’язування задач, продовжувати формувати вміння працювати з підручником. Форми роботи: бліцопитування, робота […]...

  29. Сума кутів трикутника Геометрія Основні властивості найпростіших геометричних фігур Сума кутів трикутника Теорема. Сума кутів трикутника дорівнює . Із цієї теореми випливають наслідки: 1. У будь-якому трикутнику принаймні два кути гострі (тобто в трикутнику не може бути більше одного прямого або тупого ­кута). 2. Кути рівностороннього трикутника дорівнюють . Зовнішнім кутом трикутника при даній вершині називається кут, суміжний […]...

  30. Нерівність трикутника Геометрія Трикутники Нерівність трикутника Теорема. Які б не були три точки, відстань між будь-якими двома із цих точок не більша, ніж сума відстаней від них до третьої точки. Звідси випливає, що у будь-якому трикутнику кожна сторона менша за суму двох інших сторін, але більша за модуль різниці двох інших сторін. Якщо a, b і c […]...

  31. Відрізок і його довжина § 1. Найпростіші геометричні фігури та їхні властивості 2. Відрізок і його довжина Практичні завдання 20. Точки С, D, Е належать відрізку AB, а точки F, M, K не належать відрізку АВ. 21. Утворилося три відрізки АВ, ВС, АС. 22. Точка С лежить між точками А і В, а точка D – між точками В […]...

  32. Рівняння. Кути. Трикутники УРОК 42 Тема. Рівняння. Кути. Трикутники Мета: перевірити рівень засвоєння учнями навчального матеріалу; перевірити рівень сформованості вмінь учнів: вимірювати і будувати кути за допомогою транспортира; обчислювати невідомі сторони й периметр трикутника; розв’язувати рівняння з використанням правил знаходження невідомих компонентів дій додавання і, віднімання. Тип уроку: контроль знань. Хід уроку І. Тематична контрольна робота № 3 […]...

  33. Ознаки паралельності прямих. Сума кутів трикутника Урок № 40 Тема. Ознаки паралельності прямих. Сума кутів трикутника Мета: перевірити рівень засвоєння знань та вмінь, передбачених програмою, із зазначених тем. Тип уроку: контроль та корекція знань. ХІД УРОКУ I. Організаційний момент II. Перевірка домашнього завдання Зібрати зошити з виконаною домашньою контрольною роботою. Роботу оцінити та врахувати в тематичному балі. III. Умова контрольної роботи […]...

  34. Тотожно рівні вирази. Тотожності 132. 1) Переставна властивість додавання; 2) сполучна властивість додавання; 3) переставна властивість множення; 4) переставна властивість множення і додавання; 5) розподільна властивість множення. 133. 1) 2х – 12 = 2(х – 6) – тотожність; 2) а – b = -(b – а) – тотожність; 3) 3m + 9 = 3(m + 9) – не є […]...

  35. Співвідношення між сторонами й кутом прямокутного трикутника Геометрія Трикутники Співвідношення між сторонами й кутом прямокутного трикутника Нехай ABC – прямокутний трикутник з прямим кутом С і гострим кутом при вершині A, що дорівнює . Косинусом гострого кута прямокутного трикутника називається відношення при­лег­лого катета до гіпотенузи. На рисунку або . Синусом кута називається відношення протилежного катета до гіпотенузи: або . Тангенсом кута називається […]...

  36. Теорема Гульдіна 1379. У трикутнику ABC AB = ВС, AC = a, BK + AC, BK = h. Центром мас трикутника ABC є точка O – точка перетину медіан трикутника ABC: Тоді і Відповідь: 1380. ABCD – ромб, AB = a, ∠BAD = a, BD? I. SABCD = AB2 sin∠BAD = а2 sin α. Центром мас ромба […]...

  37. Коло і його елементи Розділ 4. Коло і круг. Геометричні побудови § 21. Коло і його елементи 578. PL – хорда, що проходить через центр кола, називається діаметром. 579. 1) 5 х 2 = 10(см); 2) 4,7 х 2 = 9,4 (дм). 580. 1) 8 мм х 2 = 16 мм; 2) 4,8 см х 2 = 7,6 см. […]...

  38. Вправи 475-524 475. ?ABC – прямокутний; ∠A = 30°; АС = 18 см; ВК – бісектриса, проведена до катета АС; ∠CBK = ∠ABK = ∠CBA : 2 = 60° : 2 = 30°; ∠CBA = 90° – ∠CAB = 90° – 30° = 60°; СК = х, тоді AK = 18 – х. ?АВК – прямокутний; ∠A […]...

  39. Площа трикутника Урок № 47 Тема. Площа трикутника Мета: домогтися засвоєння учнями змісту та ідеї доведення теореми про формулу плоті трикутника й наслідків з неї. Сформувати вміння: – відтворювати зміст вивчених формул; – записувати формули відповідно до заданих позначень елементів трикутників; – застосовувати вивчені формули до розв’язування задач. Тип уроку, засвоєння вмінь та навичок. Наочність та обладнання: […]...

  40. Середня лінія трикутника Геометрія Трикутники Середня лінія трикутника Середньою лінією трикутника називається відрізок, який сполучає середини двох його сторін. Теорема 1. Середня лінія трикутника, яка сполучає середини двох його сторін, паралельна третій стороні й дорівнює її половині. На рисунку праворуч: ;. У трикутнику можна провести три середні лінії. Вони утворюють трикутник з такими ж кутами, як даний, і […]...

Ви зараз читаєте: Рівні трикутники. Висота, медіана, бісектриса трикутника
«
»