Розв’язування задач за допомогою систем лінійних рівнянь
Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ
& 30. Розв’язування задач за допомогою систем Лінійних рівнянь
Ми вже розглядали задачі, які можна розв’язати за допомогою рівнянь. Математичною моделлю задачі може бути не тільки рівняння, а й система рівнянь. Зазвичай це має відношення до тих задач, де невідомими є значення двох або більшої кількості величин.
Приклад 1. За 7 шоколадних батончиків і 2 плитки шоколаду заплатили 59 грн. Скільки коштує батончик і скільки плитка шоколаду, якщо відомо, що три батончики дорожчі за одну плитку
Р о з в ‘ я з а н н я. Нехай батончик коштує х грн, а плитка шоколаду – у грн. Тоді сім батончиків коштують 7х грн, а дві плитки шоколаду – 2у грн. Оскільки ралом за таку кількість батончиків і плиток шоколаду заплатили 59 грн, маємо рівняння: 7х + 2у = 59.
Вартість трьох батончиків складає 3х грн, і вони дорожчі за плитку шоколада на 3 грн. Тому одержимо ще одне рівняння: 3х – у = 3.
Щоб відповісти на запитання задачі, ми маємо знайти такі значення х і у, які б задовольняли обидва рівняння, тобто задовольняли систему рівнянь:
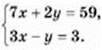
Розв’язавши цю систему, одержимо, що х = 5; у
В і д п о в і д ь: 5 грн; 12 грн.
Зауважимо, що цю задачу, як і деякі інші із цього параграфа, можна розв’язати і за допомогою рівняння з однією змінною. Але часто скласти систему рівнянь до задачі простіше, ніж скласти до неї рівняння з однією змінною.
Розв’язуючи задачу за допомогою системи рівнянь, слід дотримуватися такої послідовності дій:
1) позначити деякі дві невідомі величини змінними (наприклад, х і у);
2) за умовою задачі скласти систему рівнянь:
3) розв’язати одержану систему:
4) проаналізувати знайдені значення змінних відповідно до умови задачі, дати відповідь на запитання задачі;
5) записати відповідь.
Приклад 2. За 2 год проти течії і 5 год за течією моторний човен долає 120 км. За 2 год за течією і 1 год проти течії цей самий човен долає 51 км. Знайти власну швидкість човна і швидкість течії.
Р о з в ‘ я з а н н я. Нехай власна швидкість човна х км/год, а швидкість течії – у км/год. Тоді швидкість човна за течією річки дорівнює (х + у) км/год, а швидкість човна проти течії (х – у) км/год. За 5 год за течією човен проходить 5(х + у) км, за 2 год проти течії – 2(х – у) км, а разом це складає 120 км. Маємо рівняння: 5(х + у) + 2(х – у) = 120.
Міркуючи аналогічно, можна за умовою задачі скласти ще одне рівняння: 2(х + у) + (х – у) = 51.
Маємо систему рівнянь
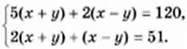
Розв’язавши яку, одержимо:
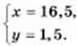
Отже, власна швидкість човна – 16,5 км/год, а швидкість течії – 1,5 км/год.
В і д п о в і д ь: 6,5 км/год; 1,5 км/год.
Якої послідовності дій слід дотримуватися, розв’язуючи задачу за допомогою системи рівнянь?
1079. У легкоатлетичній секції тренуються 32 спортсмени, причому дівчат серед них на 4 більше, ніж хлопців. Скільки дівчат і скільки хлопців тренується в цій секції?
1080. За дві години кухар наліпив 260 пельменів, причому за першу годину – на 20 пельменів менше, ніж за другу. Скільки пельменів наліпив кухар за першу годину і скільки за другу?
1081. За олівець і три зошити заплатили 8,8 грн, а за три олівці і зошит – 7,2 грн. Скільки коштує один олівець і скільки один зошит?
1082. За 2 год пішки і 1 год па велосипеді турист подолав 18 км, а за 1 год пішки і 2 год на велосипеді – 27 км. З якою швидкістю турист рухався пішки і з якою па велосипеді?
1083. У касі крамниці після переобліку залишилося 12 монет по 25 і 50 копійок, усього на суму 4 гривні. Скільки монет по 25 копійок і скільки по 50 копійок залишилося в касі?
1084. Було придбано 16 зошитів у клітинку і лінійку, усього на суму 32 грн 80 коп. Зошит у клітинку коштує 2 грн 20 коп., а в лінійку – 1 грн 80 коп. Скільки зошитів в клітинку і скільки в лінійку було придбано?
1085. За 3 футбольних і 2 волейбольних м’ячі заплатили 544 грн. Скільки коштує футбольний м’яч і скільки волейбольний, якщо два волейбольних м’ячі на 96 грн дорожчі за один футбольний?
1086. 2 акумулятори і 5 батарейок разом коштують 85,5 грн. Скільки коштує один акумулятор і скільки одна батарейка, якщо акумулятор коштує стільки ж, скільки 26 батарейок?
1087. Основа рівнобедреного трикутника на 2 см більша за його бічну сторону. Знайдіть сторони трикутника, якщо його периметр дорівнює 26 см.
1088. Довжина прямокутника на 8 м більша за ширину. Знайдіть довжину і ширину прямокутника, якщо його периметр дорівнює 56 м.
1089. Човен за 3 год руху за течією і 2 год руху проти течії долає 92 км. За 9 год руху за течією човен долає відстань у 5 разів більшу, ніж за 2год руху по озеру. Знайдіть власну швидкість човна та швидкість течії.
1090. Човен рухався 2 год за течією і 5 год проти течії, подолавши за цей час 110 км. Швидкість човна проти течії складає 70 % від швидкості човна за течією. Знайдіть власну швидкість човна та швидкість течії.
1091. З пунктів А і В, відстань між якими 168 км, одночасно вирушають велосипедист і мотоцикліст. Якщо вони будуть рухатися назустріч один одному, то зустрінуться через 3 год. А якщо рухатимуться в одному напрямі, то мотоцикліст наздожене велосипедиста через 6 год. Знайдіть швидкість кожного з них.
1092. Сума двох чисел дорівнює 62. Знайдіть кожне із чисел, якщо 70 % від одного і 60 % від другого разом складають 39,6.
1093. 20 % від одного числа на 2,4 більше за 10 % від другого. Знайдіть ці числа, якщо їх сума дорівнює 72.
1094. Матері разом з донькою 42 роки. Через рік мати стане втричі старшою за доньку. Скільки років кожній з них зараз?
1095. Розв’яжіть систему рівнянь. Складіть задачу, яка б розв’язувалася за допомогою цієї системи:
1096. Розв’яжіть систему рівнянь. Складіть задачу, яка б розв’язувалася за допомогою цієї системи:
1097. У ящику і кошику разом 95 яблук. Якщо кількість яблук у ящику зменшити вдвічі, а кількість яблук у кошику збільшити на 25, то яблук у ящику і кошику стане порівну. Скільки яблук у ящику і скільки в кошику?
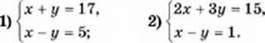
1098. Сума двох чисел дорівнює 45. Знайдіть ці числа, якщо 60 % від одного з них дорівнюють 75 % від другого.
1099. Знайдіть два числа, якщо їх сума дорівнює 200 і 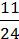 від одного з них дорівнюють
від одного з них дорівнюють  від другого.
від другого.
1100. Змішали два види цукерок вартістю 45 грн і 54 грн за кілограм, після чого утворилося 25 кг суміші вартістю 48 грн 96 коп. за кілограм. По скільки кілограмів цукерок кожного виду взяли для суміші?
1101. З двох сортів печива вартістю 24 грн і 30 грн за кілограм утворили 40 кг суміші вартістю 26 грн 70 коп. за кілограм. По скільки кілограмів печива кожного виду взяли?
1102. У двох бідонах разом було 75 л олії. Після того як половину олії з першого бідона перелили в другий, олії в другому стало в 4 рази більше, ніж у першому. По скільки олії було в кожному бідоні спочатку?
1103. На двох полицях разом 57 книжок. Після того як з першої полиці переставили 5 книжок на другу, книжок на другій полиці стало вдвічі більше, ніж на першій. По скільки книжок було на кожній полиці спочатку?
1104. За 5 світильників і 4 ліхтарики заплатили 536 грн. Після того як світильники подешевшали на 15 %, а ліхтарики подорожчали на 10 %, один світильник і один ліхтарик разом стали коштувати 118 грн. Якою була початкова вартість світильника і якою – ліхтарика?
1105. Два кондитерських цехи за день мали разом виготовити 300 тортів. Коли перший цех виконав 55 % свого завдання, а другий – 60 % свого, виявилося, що перший цех виготовив на 27 тортів більше, ніж другий. По скільки тортів мав виготовити кожен цех?
1106. Якщо чисельник даного дробу збільшити на 7, то дріб дорівнюватиме  . Якщо ж знаменник даного дробу збільшити на 2, то дріб дорівнюватиме 0,25. Знайдіть цей дріб.
. Якщо ж знаменник даного дробу збільшити на 2, то дріб дорівнюватиме 0,25. Знайдіть цей дріб.
1107. Якщо чисельник дробу зменшити на 2, то дріб дорівнюватиме 0,5. Натомість, якщо знаменник дробу збільшити на 11, то дріб дорівнюватиме . Знайдіть цей дріб.
. Знайдіть цей дріб.
1108. По скільки грамів кожного з 2%-го і 6%-го розчинів солі треба взяти, щоб з них одержати 200 г 5%-го розчину?
1109. В одному сплаві міститься 9 % цинку, а в другому – 24 %. По скільки грамів кожного сплаву треба взяти, щоб одержати зливок масою 260 г, що містить 15 % цинку?
1110. Чотири роки тому батько був у 8 разів старший за сина, а через 20 років батько стане удвічі старший за сина. Скільки років кожному з них зараз?
1111. Якщо суму цифр двоцифрового числа збільшити в 5 разів, то вона дорівнюватиме самому числу. А якщо його цифри поміняти місцями, то воно збільшиться на 9. Знайдіть дане число.
Вправи для повторення
1112. Розкладіть на множники многочлен:
1) m2 + 10m + 25;
2) с2 – 8с + 16;
3) р2 – 0,36;
4) 49а2 + b2.
1113. Спростіть вираз:
1) 2х(3х – 4х3) – (x + 3х2)2;
2) 2p2(2p2 – 6pm) – (2р2 – 3mр)2.
1114. Побудуйте графік функції:
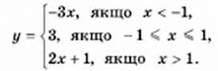
Цікаві задачі для учнів неледачих
1115. Дано п’ять різних додатних чисел, які можна розбити на дві групи так, щоб суми чисел у кожній з груп були однаковими. Скількома способами це можна зробити?
Домашня самостійна робота № 6
Кожне завдання має по чотири варіанти відповідей (А – Г), серед яких лише один є правильним. Оберіть варіант правильної відповіді.
1. Укажіть рівняння, що є лінійним рівнянням з двома змінними.
A) 2х2 -3у = 4;
Б) 2х – 3у + 7z = 4;
B) 2х – 3у = 4;
Г) 2х – у3 = 4.
2. Укажіть точку, що належить графіку рівняння х + у = 6.
А) (2; 3);
Б) (2; 4);
В) (3; 4);
Г) (-2; -4).
3. Укажіть пару чисел, що є розв’язком системи рівнянь 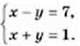
А) (4; 3);
Б) (-4; 3);
В) (-4; -3);
Г) (4; -3).
14. Розв’яжіть графічним способом систему рівнянь 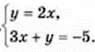
A) (1; 2);
Б) (-1; -2);
B) (-2; -1);
Г) система не має розв’язків.
5. Розв’яжіть способом підстановки систему рівнянь 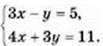
А) (2; 1);
Б) (1; 2);
В) (3; 1);
Г) (1; 3).
6. Розв’яжіть способом додавання систему рівнянь 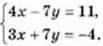
А) (1; 1);
Б) (-1; 1);
В) (-1; -1);
Г) (1; -1).
7. Пара чисел (-3; m) є розв’язком рівняння 4х – у = 7. Знайдіть m.
А) 5;
Б)-5;
В) 19;
Г) 19.
8. На графіку рівняння 3у – 2х = 5 взято точку з абсцисою -1. Знайдіть ординату цієї точки.
А) 1;
В) -1;
В) 2  ;
;
Г)-4.
9. З пунктів А і В, відстань між якими 60 км, вирушили одночасно пішохід і велосипедист. Якщо вони рухатимуться назустріч один одному, то зустрінуться через 3 год, а якщо вони рухатимуться в одному напрямі, то велосипедист наздожене пішохода через 5 год. Знайдіть швидкість пішохода.
А) 3 км/год;
Б) 4 км/год;
В) 4,5 км/год;
Г) 5 км/год.
10. Скільки спільних точок мають графіки рівнянь х + 2у = -2 і 2х + 4у = -8?
А) жодної;
Б) одну;
В) дві;
Г) безліч.
11. Графік функції у = kx + l перетинає осі координат в точках (0; -2) і (3; 0). Знайдіть k.
А) -2;
Б) 0;
В)  ;
;
Г) –  .
.
12. При якому значенні а система рівнянь 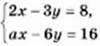 має безліч розв’язків?
має безліч розв’язків?
А) 0;
Б) 2;
В) -4;
Г) 4.
ЗАВДАННЯ ДЛЯ ПЕРЕВІРКИ ЗНАНЬ ДО & 25 – & 30
1. Яке з рівнянь є лінійним рівнянням з двома змінними:
1) 2х + 3у = 9;
2) 2х + 3у2 = 9?
2. Чи є розв’язком рівняння 2х + у = 7 пара чисел:
1) (3; -5);
2) (4; -1)?
3. Чи є розв’язком системи рівнянь 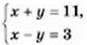 пара чисел:
пара чисел:
1) (6; 5);
2) (7; 4)?
4. Розв’яжіть графічно систему рівнянь 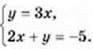
5. Розв’яжіть способом підстановки систему рівнянь 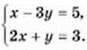
6. Розв’яжіть способом додавання систему рівнянь 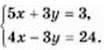
7. Знайдіть розв’язок системи 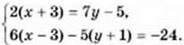
8. За 8 зошитів і 3 блокноти заплатили 9 грн 30 коп. Після того як зошит подорожчав на 15 %, а блокнот подешевшав на 10 %, за один зошит і один блокнот заплатили 2 грн 04 коп. Знайдіть, якою була початкова ціна зошита і якою блокнота?
Додаткові вправи
9. Побудуйте графік рівняння 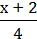 +
+ 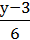 = –
= – 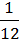 .
.
10. Графік функції у = kx + l проходить через точки (3; -4) і (-12; -9). Знайдіть k і l.
11. При якому значенні а система рівнянь 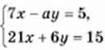 має безліч розв’язків?
має безліч розв’язків?
Вправи для повторення розділу З
До & 22
1116. Чи є число -5 коренем рівняння:
1) х + 3 = 2;
2) 2 – х = 7;
3) х : 5 = 1;
4) 4х = -20?
1117. Доведіть, що кожне із чисел 2, -3 і 0 є коренем рівняння х(х – 2)(х – 3) = 0.
1118. Чи є рівносильними рівняння:
1)|х| = 2 і х(х + 2) = 0;
2)|х| = 4 і х2 = 16?
1119. Чи є правильним твердження: “Якщо кожен корінь одного рівняння є коренем іншого, то ці рівняння рівносильні”?
До & 23
1120. Укажіть кількість коренів рівняння:
1) 7х = -12;
2) 0х = 0;
3) -3х = -17;
4) 0х = -8.
1121. Розв’яжіть рівняння:
1) – х = 6;
х = 6;
2)  Х =
Х = 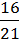 ;
;
3) х –  = 3;
= 3;
4)  +
+  = 15;
= 15;
5) 4,7х – 2 = 4,5х + 3;
6) 2х – 3 – (3х – 2) = -8.
1122. Знайдіть корінь рівняння:
1) 10(2х – 7) – 5(4х – 2) = -60;
2) 3(5х – 4) – (15х – 2) = 9;
3) 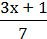 +
+ 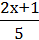 = 2;
= 2;
4)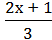 –
– 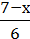 =
= 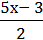
1123. При якому значенні а:
1) рівняння ах = 8 не має коренів;
2) коренем рівняння (а + 3)х – а + 3 є будь-яке число?
1124. Розв’яжіть рівняння (а – 1)х = 8 відносно змінної х.
До &24
1125. За 3 дні було відремонтовано х автомобілів. Виразіть через х кількість відремонтованих автомобілів за день.
1126. Периметр прямокутника дорівнює 36 см, причому його довжина вдвічі більша за ширину. Знайдіть сторони прямокутника та його площу.
1127. За 7 олівців і 3 ручки заплатили 16 грн 95 коп. Скільки коштує один олівець, якщо він дешевший за ручку на 1 грн 65 коп.?
1128. У кошику було в 4 рази менше винограду, ніж в ящику. Після того як з ящика до кошика переклали 1,5 кг винограду, у кошику стало втричі менше винограду, ніж в ящику. Скільки кілограмів винограду було в кошику і скільки в ящику спочатку?
1129. За 4,5 год човен за течією річки долає таку саму відстань, як за 6 год проти течії. Знайдіть швидкість течії, якщо власна швидкість човна дорівнює 14 км/год.
1130. На проміжній станції потяг було затримано на 0,5 год. Збільшивши швидкість на 15 км/год, він через 2 год прибув на кінцеву станцію чітко за розкладом. Якою була швидкість потяга до затримки?
1131. На двох тарілках було по 60 вареників. Після того як з першої тарілки з’їли утричі більше вареників, ніж з другої, на ній залишилося вдвічі менше вареників, ніж на другій. По скільки вареників залишилося на кожній тарілці?
1132. Для преміювання працівників офісу нарахували певну суму коштів. Якщо кожен отримає по 1100 грн, то 200 грн ще залишаться, а для того, щоб кожен отримав по 1200 грн, не вистачить 600 грн. Скільки працівників в офісі та яку суму коштів нарахували для преміювання?
1133. В одній овочевій ятці з а планували продати 95 кг лимонів, а в другій – 60 кг. Перша щодня продавала по 7 кг, а друга – по 6 кг. Через скільки днів лимонів у першій ятці залишиться вдвічі більше, ніж у другій?
1134. Змішали 15%-й розчин добрива з 5%-м і одержали 180 г 7,5% – го розчину. По скільки грамів кожного з розчинів взяли?
До & 25
1135. Чи є пара чисел (7; 1) розв’язком рівняння х – у = 6? Знайдіть що чотири розв’язки цього рівняння.
1136. Знайдіть два будь-яких розв’язки рівняння:
1) 2х + у = 4;
2) х – 3у = 7.
1137. Виразіть:
1) змінну у через змінну х з рівняння 7х – у = 18;
2) змінну х через змінну у з рівняння 3х + 9у = 0;
3) змінну у через змінну х з рівняння 13х – 2у = 6;
4) змінну х через змінну у з рівняння 8х + 15у = 24.
1138. Замініть зірочку числами так, щоб кожна з пар (*; 3); (6; *); (*; -3); (18; *) була розв’язком рівняння х – 3у – 9.
1139. Доведіть, що рівняння з двома змінними не має розв’язків:
1) х2 + у2 = -4;
2) |х| + у2 + 1 = 0;
3) |х| – |у| = 5;
4) 2х4 + 3|у| = -2.
1140. Знайдіть усі пари цілих чисел, які с розв’язками рівняння |х| + |у| = 2.
До &26
1141. Побудуйте графік рівняння:
1) х – у – 1;
2) 1,5х + у = 7;
3) х – 4у = 5;
4) 0,1х + 0,2у = 2.
1142. Побудуйте в одній координатній площині графіки рівнянь х + у = 5 і 7х – 4у = 2. Знайдіть координати точки їх перетину. Переконайтеся, що знайдена пара є розв’язком кожного з рівнянь.
1143. Ордината деякої точки прямої, що є графіком рівняння 9х + 5у = 27, дорівнює нулю. Знайдіть абсцису цієї точки.
1144. Побудуйте графік рівняння:
1) |х| + у = 0;
2) |х| + х – у = 0.
1145. Побудуйте ту частину графіка рівняння 2х + у = 4, яка розташована в першій координатній чверті.
До& 27
1146. Чи є розв’язком системи рівнянь 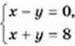 пара чисел:
пара чисел:
1) х = 5; у = 5;
2) х = 4; у = 4?
1147. Розв’яжіть графічно систему рівнянь:
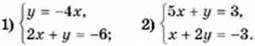
1148. Розв’яжіть систему рівнянь графічно:
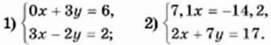
1149. При якому значенні а система рівнянь:
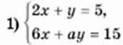 має безліч розв’язків;
має безліч розв’язків;
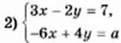 не має розв’язків?
не має розв’язків?
До & 28
1150. Розв’яжіть систему рівнянь способом підстановки:

1151. Не викопуючи побудови, знайдіть координати точки перетину графіків рівнянь:
1) 2х + 3у = 0 і 4х – 5у = -22;
2) 4х – 7у = 34 і 2х + 7у = -4.
1152. Розв’яжіть систему рівнянь:
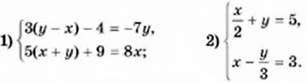
1153. Розв’яжіть систему рівнянь:
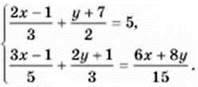
1154. Розв’яжіть рівняння з двома змінними:
1) |х – у | + (х + 2у – 1)2 = 0;
2) |х + у – 6| + х2 – 4ху + 4у2 = 0.
До & 29
1155. Розв’яжіть систему рівнянь способом додавання:

1156. Розв’яжіть систему рівнянь способом додавання:
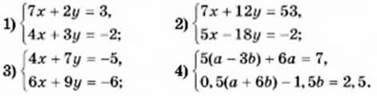
1157. Скільки розв’язків залежно від коефіцієнта а має система рівнянь 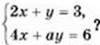
До & 27-29
1158. Розв’яжіть систему рівнянь трьома способами (графічним, підстановки, додавання):
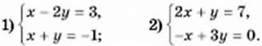
1159. Знайдіть розв’язок системи рівнянь:
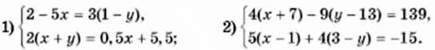
1160. Розв’яжіть систему рівнянь:
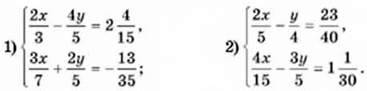
1161. Розв’яжіть систему рівнянь:

1162. Чи є розв’язок система рівнянь:
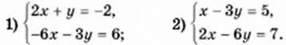
1163. Чи має розв’язок система рівнянь:
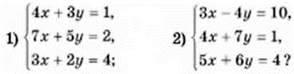
1164. Графік прямої у = kx + l перетинає вісь х у точці з абсцисою 4, а вісь у – у точці з ординатою -5.
1) Задайте функцію формулою.
2) З’ясуйте, чи проходить її графік через точку ( 80; -105).
1165. Розв’яжіть систему рівнянь:
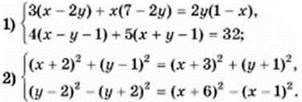
1166. При якому значенні а система 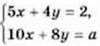 1) має безліч розв’язків;
1) має безліч розв’язків;
2) не має розв’язків?
Чи існує таке значення а, при якому система має єдиний розв’язок?
1167. При якому значенні b система 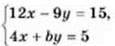
1) має безліч розв’язків;
2) мас єдиний розв’язок? Знайдіть цей розв’язок.
До & 30
1168. За 3 год автобусом і 5 год потягом турист подолав 450 км. Знайдіть швидкість автобуса і швидкість потяга, якщо швидкість потяга на 10 км/год більша за швидкість автобуса.
1169. За 7 порцій млинців і 2 салати заплатили 156 грн. Скільки коштує одна порція млинців і скільки – один салат, якщо дві порції млинців на 9 грн дешевші за три салати?
1170. Теплохід за 3 год за течією і 2 год проти течії долає 142 км. Цей самий теплохід за 4 год проти течії долає на 14 км більше, ніж за 3 год за течією. Знайдіть власну швидкість теплохода і швидкість течії.
1171. Майстер і його учень повинні були виготовити 114 деталей. Після того як учень пропрацював 2 год, до роботи приєднався майстер, і вони разом закінчили виготовлення деталей за 3 год. Скільки деталей за годину виготовляв майстер і скільки учень, якщо майстер за 2 год виготовляє стільки ж деталей, скільки учень за 3 год?
1172. Два кошики наповнено грушами. Якщо з другого кошика перекласти в перший 10 груш, то в обох кошиках груш стане порівну. Якщо ж з першого кошика перекласти в другий 44 груші, то груш у першому кошику залишиться в 4 рази менше, ніж у другому. Скільки груш у кожному кошику?
1173. Різниця між половиною одного числа і 0,75 другого дорівнює 8. Якщо перше число зменшити на свою сьому частину, а друге збільшити на свою дев’яту частину, то їх сума становитиме 100. Знайдіть дані числа.
1174. Сума трьох чисел, з яких друге в 5 разів більше за перше, дорівнює 140. Якщо друге число збільшити на 15 %, трете – зменшити на 10 %, а перше не змінювати, то сума цих чисел становитиме 139,5. Знайдіть дані числа.
1175. Периметр прямокутника на 154 см більший за одну з його сторін і на 140 см більший за другу. Знайдіть площу прямокутника.
1176. Сума цифр деякого двоцифрового числа дорівнює 8. Якщо його цифри поміняти місцями, то одержимо число, що на 18 більше за дане. Знайдіть дане число.
1177. У двох бідонах ємністю 20 л і 15 л вже є певна кількість молока. Якщо більший бідон долити до краю молоком з меншого, то в меншому залишиться половина початкової кількості. Якщо ж долити менший бідон до краю молоком з більшого, то в більшому залишиться  від початкової кількості. По скільки літрів молока в кожному бідоні?
від початкової кількості. По скільки літрів молока в кожному бідоні?
