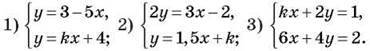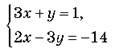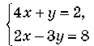СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ З ДВОМА ЗМІННИМИ. ГРАФІЧНИЙ СПОСІБ РОЗВ’ЯЗАННЯ СИСТЕМ
Цілі:
– навчальна: сформувати поняття системи двох лінійних рівнянь з двома змінними, розв’язку системи двох лінійних рівнянь з двома змінними; сформувати вміння розв’язувати системи рівнянь графічним способом;
– розвивальна: формувати вміння аналізувати інформацію; розвивати увагу, логічне мислення, пам’ять;
– виховна: виховувати наполегливість у досягненні мети, зацікавленість у пізнанні нового, скрупульозність;
Тип уроку : засвоєння нових знань, умінь, навичок.
Обладнання та наочність:
Хід уроку
І.
______________________________________________________
______________________________________________________
______________________________________________________
ІІ. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ
1. Перевірка завдання, заданого за підручником
______________________________________________________
______________________________________________________
2. Бліцопитування
З-поміж наведених рівнянь виберіть те, графіком якого є:
A) пряма, яка проходить через точку A (-2; 3);
Б) пряма, яка проходить через початок координат;
B) пряма, паралельна осі Oy;
Г) пряма, паралельна осі Ox;
Д) уся координатна площина.
Доведіть, що рівняння, яке залишилося, не має розв’язків.
Варіант | Варіант 2 |
2y + 5х = 2(y + 1) | 3(x + 1) = 2у + 3 |
2х + у = -1 | -2x + 4у = 2(3 – х) |
X + 3у – 6 = 3(у – 2) + x | 2х – у = -7 |
2x + 6у + 4 = 2(x + 3у) | -2у + 3х = 2(5 – у) |
X + 2 = 2(у +1) | Х + у = 3 + у + х |
3(x – 5) = 5у + 3х | У + 2х – 8 = у + (х – 4) • 2 |
ІІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ
Виконання графічних вправ
Побудуйте в одній координатній площині графіки рівнянь:
1) 3x – 2у = 0 і 2x – у = 1; 2) y – 2х = 1 і 2y – 4х = 6; 3) 2x + 3у = 5 і 4x + 6у = 10. Знайдіть координати точок перетину цих графіків.
План вивчення теми
1. Задачі, що приводять до поняття системи рівнянь.
2. Означення розв’язку системи рівнянь.
3. Що означає розв’язати систему рівнянь?
4. Графічний спосіб розв’язання систем рівнянь із двома змінними.
5. Кількість розв’язків системи двох лінійних рівнянь із двома змінними.
______________________________________________________
______________________________________________________
IV. ЗАСВОЄННЯ НОВИХ ЗНАНЬ І ВМІНЬ
1. Робота за підручником
______________________________________________________
______________________________________________________
2. Додаткові завдання
1) Розв’яжіть графічно систему рівнянь. Відповідь дайте з точністю до 0,1:
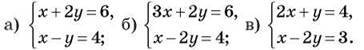
2) З’ясуйте, чи мають розв’язки системи рівнянь:
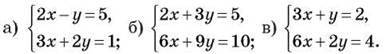
3) До рівняння 6х – у = 8 підберіть друге рівняння так, щоб дістати систему рівнянь, яка:
А) має єдиний розв’язок; б) має безліч розв’язків; в) не має розв’язків.
V. ПІДСУМКИ УРОКУ
1.
______________________________________________________
______________________________________________________
2. Самостійна робота з подальшою взаємоперевіркою
Варіант 1 | Варіант 2 |
1) Розв’яжіть графічно систему рівнянь | |
|
|
За допомогою підстановки в рівняння значень х і у переконайтеся, що вони задовольняють обидва рівняння | |
2) Напишіть яку-небудь систему рівнянь, яка має розв’язок | |
(5; -1) | (-2; 5) |
VI. ДОМАШНЄ ЗАВДАННЯ
1. Завдання за підручником:
______________________________________________________
______________________________________________________
2. Додаткове завдання. Підберіть, якщо це можливо, таке значення k, при якому система рівнянь має один розв’язок; не має розв’язків; має безліч розв’язків: