Властивості й ознака рівнобедреного трикутника

Розділ 1. Найпростіші геометричні фігури та їх властивості

§ 12. Властивості й ознака рівнобедреного трикутника

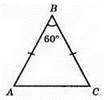
476. На мал. 72: ML і МК – бічні сторони, KL – основа, ∠K = ∠L.

477. KD = DF, КЕ = EF, ∠K = ∠F, ∠KDE = ∠FDE, ∠DEK = ∠DEF = 90°.

478.

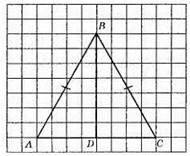
Щоб провести бісектрису, медіану і висоту до основи трикутника, досить поділити основу навпіл і з’єднати середину з точкою В.

479. ?ABC – рівнобедрений, бо ∠C = ∠B. Бічні сторони АС і AB, основа СВ.

480.

480.

Оскільки

бісектриса MN є медіаною, то KN = NL. Отже:

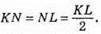
481.

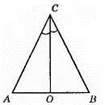
Бісектриса СО є медіаною, тому AB = 2АО = 2BO.

1) AB = 2АО = 2 х 0,7 дм = 1,4 дм;

2) AB = 2BO = 2 x 25 мм = 50 мм.

482.

1) Якщо DF = DE + FE, то FA не є медіаною.

2) Якщо EF = ED ≠ DF, то FA не є медіаною.

3) Якщо FD = FE ≠ DE, то FA не є медіаною, згідно з властивістю рівнобедреного трикутника.

483. 1)

∠CKA = ∠CKB = 90°;

2)

∠AKB = ∠AKC = 90°;

3)

∠BKA = ∠BKC = 90°.

484. 1) a ⊥ ON

2) a ⊥ MN

3) а ⊥ ОМ

485. Мал. 276. ∠C = ∠B = 180° – 135° = 45°, ∠А = 135° – 45° = 90°.

Мал. 277. ∠ВАС = 75° – як вертикальні кути. ∠C = ∠А = 75°, ∠В = 180° – 2 х 75° = 180° – 150° = 30°.

486.

Якщо кут при основі дорівнює а, то кут при вершині дорівнює 180° – 2α.

1) 180° – 2 х 40° = 180° – 80° = 100°;

2) 180° – 2 х 65° = 180° – 130° = 50°;

3) 180° – 2 x 80° = 180° – 160° = 20°.

Відповідь: 1) 100°; 2) 50°; 3) 20°.

487.

Якщо кут між бічними сторонами дорівнює а, то кути при основі дорівнюють

Відповідь: 1) 54° і 54°; 2) 45° і 45°; 3) 30° і 30°.

488.

Нехай у трикутнику KLM ∠L = 90°, KL = LM, тоді

Відповідь: 90°, 45°, 45°.

489.

Оскільки в трикутнику проти рівних сторін лежать рівні кути, то в рівносторонньому трикутнику ∠К = ∠L = ∠М.

490. Див. № 489.

∠K = ∠L = ∠M = 180°/3 = 60°.

Відповідь: 60°, 60°, 60°.

491. І випадок

Нехай? ABC – рівнобедрений, AB = ВС, ∠B = 60°.

Доведемо, що? ABC – рівносторонній.

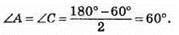
Оскільки в трикутнику всі кути дорівнюють 60°, то він рівносторонній.

II випадок

Нехай? ABC – рівнобедрений, AB = ВС, ∠A = 60°.

Доведемо, що? ABC – рівносторонній. ∠C = ∠A = 60° за властивістю рівнобедреного трикутника, тоді ∠B = 180° – ∠A – ∠C= 180° – 60° – 60° = 60°. Оскільки в трикутнику всі кути дорівнюють 60°, то? ABC – рівносторонній.

492. 1)

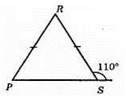
∠RSP = 180° – 110° = 70° (за властивістю суміжних кутів).

∠P = ∠RSP = 70° (за властивістю рівнобедреного трикутника).

∠R = 110° – 70° = 40° (за властивістю зовнішнього кута).

2)

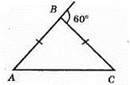
∠ABC = 180° – 60° = 120° (за властивістю суміжних кутів).

∠A = ∠C = 60°/2 = 30° (за властивістю зовнішнього кута рівнобедреного трикутника).

Відповідь: 1) 70°, 70°, 40°; 2) 120°, 30°, 30°.

493. Кут при основі рівнобедреного трикутника може бути тільки гострим, оскільки трикутник не може мати два прямих або два тупих кути.

494. Зовнішній кут при основі рівнобедреного трикутника може бути тільки тупим.

495. Оскільки кут при основі рівнобедреного трикутника може бути тільки гострим, то за умовою задачі подано кути між бічними сторонами.

Відповідь: 1) 90°, 45°, 45°; 2) 120°, 30°, 30°; 3) 140°, 20°, 20°.

496. 1)

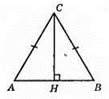
АС = ВС, AH = ВН, ∠A = ∠B, ∠ACH = ∠BCH, ∠CHA = ∠CHB.

2)

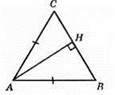
АС =АВ, СН = ВН, ∠C = ∠B, ∠CAH = ∠BAH, ∠AHC = ∠AHB.

3)

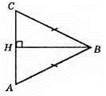
AB = CB, CH = AH, ∠C = ∠A, ∠CBH = ∠ABH, ∠BHC = ∠BHA.

497. 1)

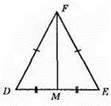
DF = EF, DM = ME, ∠DFM = ∠EFM, ∠FMD = ∠EMF, ∠D = ∠E.

2)

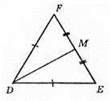
DE = DF, TM = EM, ∠FDM = ∠EDM, ∠DMF = ∠DME, ∠F = ∠E.

3)

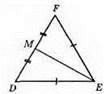
EF = ED, FM = DM, ∠FEM = ∠DEM, ∠EMF = ∠EMD, ∠F = ∠D.

498. 1) Оскільки ∠C = 180° – ∠A – ∠B = 180° – 90° – 45° = 45° і ∠C = ∠B, TO? ABC – рівнобедрений.

2) Оскільки ∠A = 180° – ∠C – ∠B = 180°- 36° – 72° = 72° і ∠A = ∠C, то? ABC – рівнобедрений.

3) Оскільки ∠B = 180° – ∠C – ∠A = 180° – 50° – 80° = 50° і ∠B = ∠C, то? АВС – рівнобедрений.

499. 1) І випадок. Якщо кут між бічними сторонами дорівнює 20°, то кути при основі дорівнюють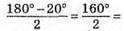

II випадок. Якщо кут при основі дорівнює 20°, то кут між бічними сторонами дорівнює 180° – 2 х 20° = 180° – 40° = 140°.

2) І випадок. Якщо кут між бічними сторонами дорівнює 40°, то кути при основі дорівнюють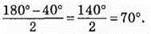

II випадок. Якщо кут при основі дорівнює 40°, то кут між бічними сторонами дорівнює 180° – 2 х 40° = 180° – 80° = 100°.

3) І випадок. Якщо кут між бічними сторонами дорівнює 80°, то кути при основі дорівнюють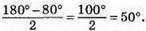

II випадок. Якщо кут при основі дорівнює 80°, то кут між бічними сторонами дорівнює 180° – 2 х 80° = 180° – 160° = 20°.

Відповідь: 1) 20°, 80°, 80° або 140°, 20°, 20°; 2) 40°, 70°, 70° або 100°, 40°, 40°; 3) 80°, 50°, 50° або 80°, 80°, 20°.

500. 1) Нехай градусна міра при основі – х°, тоді 3х° – градусна міра кута між бічними сторонами. Маємо рівняння х + х + 3х = 180°; 5х = 180°; х = 36°. Отже, кут при основі 36°, кут між бічними сторонами 108°.

2) Нехай градусна міра кута між бічними сторонами х°, тоді кут при основі – 2х°. Тоді х + 2х + 2х = 180°; 5х = 180°; х = 36°. Отже, кут між бічними сторонами дорівнює 36°, кут при основі дорівнює 72°.

Відповідь: 1) 108°, 36°, 36°; 2) 36°, 72°, 72°.

501.

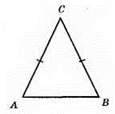
∠C = х°, тоді ∠A = ∠B = х° + n° і маємо рівняння: х + (х + n) + (х + n) = 180°; 3х + 2n = 180°, звідси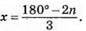

1) Якщо n = 30°, то 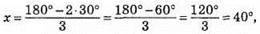тоді х + n° = 40° + 30° = 70°. Отже, кут при вершині дорівнює 40°, кути при основі по 70°.

2) Якщо n = 60°, то 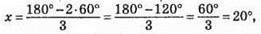тоді x + n° = 20° + 60° = 80°. Отже, кут при вершині дорівнює 20°, кути при основі по 80°.

Відповідь: 1) 40°, 70°, 70°; 2) 20°, 80°, 80°.

502. 1)

I випадок (∠B – ∠A = 15°)

Нехай ∠A = х°, тоді ∠B = х° + 15°. Маємо рівняння: х + х + х + 15° = 180°, 3х = 165°, х = 55°. Отже, ∠A = ∠C = 55°, ∠B = 70°.

II випадок (∠A – ∠B = 15°)

Нехай ∠B = x°, тоді ∠A = х° + 15°. Маємо рівняння: х + х + 15° + х + 15° = 180°, 3х + 30° = 180°, 3х = 150°, х = 50°. Отже, ∠B = 50°, ∠A = ∠C = 50° + 15° = 65°.

2)

I випадок (∠A = 2∠C)

Нехай ∠B = ∠C = х°, тоді ∠A = 2х°. Маємо рівняння: х + х + 2х = 180°, 4х = 180°, х = 45°. Отже, ∠B = ∠C – 45°, ∠A = 2 х 45° = 90°.

II випадок (∠C = 2∠A)

Нехай ∠A = х°, тоді ∠B = ∠C = 2х°. Маємо рівняння: х + 2х + 2х = 180°, 5х = 180°, х = 36°. Отже, ∠A = 36°, ∠B = ∠C = 2 x 36° = 72°.

Відповідь: 1) 55°, 55°, 70° або 65°, 65°, 50°; 2) 45°, 45°, 90° або 72°, 72°, 36°.

503. 1) I випадок

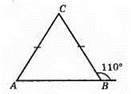
∠A = ∠B = 180° – 110° – 70° (як суміжні кути). ∠C = 110° – 70° = 40° (за властивістю зовнішнього кута трикутника).

II випадок

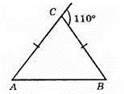
∠C= 180° – 110° = 70° (як суміжні кути).

∠A = ∠B = 110°/2 = 55° (за властивістю зовнішнього кута). Отже, кути дорівнюють 70°, 55°, 55°.

Відповідь: 70°, 70°, 40° або 70°, 55°, 55°.

2) І випадок

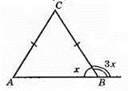
Х + 3х = 180°, 4х = 180°, х = 45°. Отже, ∠A = ∠B = 45°, ∠C = 180° – 45° – 45° = 90°. Отже, кути дорівнюють 45°, 45°, 90°.

II випадок

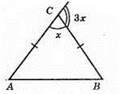
Х + 3х = 180°, 4х = 180°, х = 45°. Отже, ∠C = 45°,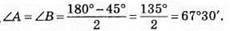

Отже, кути трикутника дорівнюють 45°, 67°30′, 67°30′.

Відповідь: 45°, 45°, 90° або 45°, 67°30′, 67°30′.

504. 1) I випадок (α ≤ 90°)

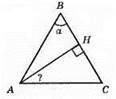
Якщо ∠B = α, тоді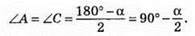

З? АНС: ∠H = 90°, тоді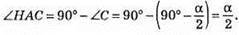

1) Якщо α = 40°, то ∠HAC = 40°/2 = 20°.

2) Якщо α = 50°, то ∠HAC = 50°/2 = 25°.

II випадок (90° < α < 180°)

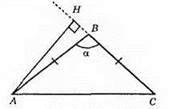
Якщо ∠B = α, тоді 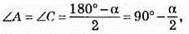∠HBA = 180° – α.

3 ?AHB: ∠HAB = 90° – (180° – α) = 90° – 180° + α = α – 90°. Тоді ∠HAC = ∠A + ∠HAB = 90° – α/2 + α – 90° = α/2.

3) Якщо α = 120°, то ∠HAC = 120°/2 = 60°.

Відповідь: 1) 20°; 2) 25°; 3) 60°.

505. 1)

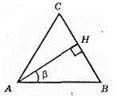
Якщо β = 25°, ∠B = 90° – 25° = 65°, ∠A = ∠B = 65°, ∠C = 180° – 130° = 50°.

2) Якщо β = 30°, то ∠B = 90° – 30° = 60°, ∠A = ∠B = 60°, ∠C = 180° – 120° = 60°.

3)

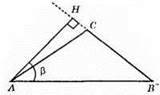
Якщо β = 60°, то з? АНВ: ∠B = 90° – 60° = 30°, ∠A = ∠B = 30°, ∠C = 180° – 30° – 30° = 120°.

Відповідь: 1) 65°, 65°, 50°; 2) 60°, 60°, 60°; 3) 30°, 30°, 120°.

506.

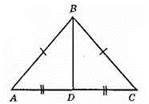
Нехай AD = DC, BD = AD, тоді? ADB і? CDB – рівнобедрені. Отже, ∠C = ∠DBC, ∠A = ∠DBA. Додамо почленно дві останні рівності ∠A + ∠C = ∠DBA + ∠DBC = ∠B. Отже, ∠A + ∠C = ∠B.

507.

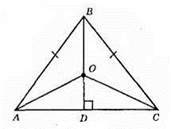
Оскільки? ABC – рівнобедрений, то AB = АС. Оскільки BD – висота, то BD є бісектрисою. Отже, ∠ABO = ∠CBO.

?АВО = ?СВО за першою ознакою рівності трикутників, оскільки AB = ВС, ВО – спільна сторона, ∠ABO = ∠CBO. Із рівності трикутників випливає, що АО = СО.

508.

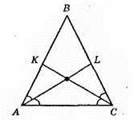
Нехай у? АBC (AB = BC) AL, CK – бісектриси. Доведемо, що AL = КС.

?ALC = ?СКА за другою ознакою рівності трикутників, оскільки ∠A = ∠C (як кути при основі рівнобедреного трикутника, АС – спільна, ∠LAC = ∠KCA – як половини рівних кутів. Із рівності трикутників випливає, що AL = СК.

509. 1) Нехай у? ABC (AB = ВС), тоді ∠A = ∠C = α. За властивістю зовнішнього кута трикутника маємо ∠DBA = ∠A + ∠C = α + α = 2α. Отже, зовнішній кут при вершині рівнобедреного трикутника вдвічі більший за кут при основі.

510.

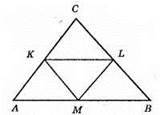
Нехай К, L, М – середини сторін рівнобедреного трикутника ABC (АС = СВ). Розглянемо трикутники АКМ і BLM. У них AM = ВМ – за умовою, AK = BL – як половини рівних сторін, ∠А = ∠B – як кути при основі рівнобедреного трикутника. Отже, ?АКМ = ?BLM. Із рівності трикутників випливає KM = LM, тобто A KLM – рівнобедрений.

511.

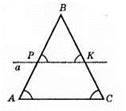
Нехай? ABC – рівнобедрений (AB = ВС), a ll АС.

Оскільки a ll АС, то ∠ВРК = ∠РАС, ∠ВКР = ∠КСА як відповідні кути при паралельних прямих a і АС і січних АР i СК). Отже, ∠А = ∠С і ∠ВРК = ∠ВКР, тобто? РВК – рівнобедрений.

512.

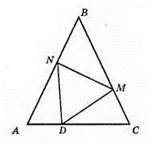
?ADN = ?CMD = ?BNM – за першою ознакою рівності трикутників, оскільки ∠А = ∠B = ∠С = 60°. AD = CM = BN (за умовою), AN = ВМ = CD (як різниці довжин сторони і відрізка AD). Із рівності трикутників випливає, що DN = NM = MD, тобто? DMN – рівносторонній.

513. 1. 1) ?АВМ = ?CBN за першою ознакою рівності трикутників, оскільки AB = АС – за умовою, BN = ВМ (за умовою), AB – спільний. Із рівності трикутників випливає, що AM = CN, ∠ВАМ =∠BCN, ∠ВМА = ∠BNC.

2) Розглянемо? ANO і? СМО. У них: AN = CM (як різниці рівних відрізків), ∠NAO = ∠МСО (за доведеним), ∠ANO = ∠СМО (як суміжні кути до рівних кутів ВМА і BNC). Отже, ?ANО = ?СМО за другою ознакою рівності трикутників.

2. 1) ?АМС = ?CNA, оскільки АС – спільна, AM = CN (за умовою), ∠АСО = ∠САО (за умовою). Із рівності цих трикутників випливає, що ∠А = ∠С, тобто? АОС – рівнобедрений.

2) Оскільки за умовою ∠АСО = ∠САО, то? АОС – рівнобедрений згідно з ознакою рівнобедреного трикутника.

3. 1) ?АОВ = ?СОВ за другою ознакою рівності трикутників, оскільки ∠АВО = ∠СВО (за умовою), ∠АОВ = ∠СОВ. (за умовою), ВО – спільна. Із рівності цих трикутників випливає, що АО = ОС, тобто? АОС – рівнобедрений.

2) Оскільки? АОС – рівнобедрений, то ∠САО = ∠АСО.

4. Оскільки АВ = ВС, то? ABC – рівнобедрений і ∠А = ∠С.

?ABD = ?СВЕ за першою ознакою рівності трикутників, оскільки AB = ВС (за умовою), AD = СЕ (за умовою), ∠А = ∠С – за доведеним. Із рівності трикутників випливає, що ∠ABD = ∠СВЕ.

5. ?ABD = ?СВЕ за другою ознакою рівності трикутників, оскільки AB = ВС (за умовою), ∠А = ∠С (за доведеним), ∠ABD = ∠СВЕ (за умовою). Із рівності цих трикутників випливає, що BD = BE, тобто? DBE – рівнобедрений, тоді ∠BDE = ∠BED.

6. ?ABD = ?СВЕ за другою ознакою рівності трикутників, оскільки AB = ВС (за умовою), ∠A = ∠C (за доведеним), ∠ABD = ∠CBE (оскільки ∠ABD = ∠ABE – ∠DBE, ∠CBE = ∠CBD – ∠DBE = ∠CBD і∠ABE – за умовою). Із рівності трикутників випливає, що AD = ЕС.

514.

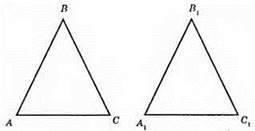
Нехай у рівнобедрених трикутників ABC (AB = ВС), A1B1C1 (A1B1 = B1C1), AC = A1C1, ∠A = ∠A1.

За властивістю рівнобедрених трикутників ∠A = ∠C, ∠A1 = ∠C1. Оскільки ∠A = ∠A1, то ∠C = ∠C1. ?ABC = ?A1B1C1 за другою ознакою рівності трикутників, оскільки АС = А1С1, ∠A = ∠A1, ∠C = ∠C1.

515. 1)

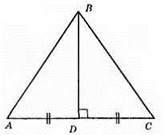
Нехай у? ABC BD ⊥ AC, AD = AC.

?ABD = ?CBD за першою ознакою рівності трикутників, оскільки AD = DC (за умовою), BD – спільна сторона, ∠ADB = ∠CDB = 90° (за умовою). З рівності трикутників випливає, що AB = ВС, тобто? ABC – рівнобедрений.

2)

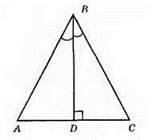
Нехай у? ABC BD ⊥ АС, ∠ABD = ∠CBD. ?ABD = ?CBD за другою ознакою рівності трикутників, оскільки BD – спільна сторона, ∠ABD = ∠CBD (за умовою), ∠BDA = ∠BDC = 90° (за умовою). З рівності трикутників випливає, що AB = ВС, тобто? ABC – рівнобедрений.

3)

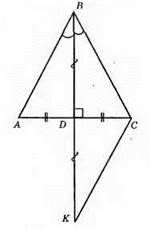
Нехай у? ABC ∠ABD = ∠CBD, AD = CD. Пpoдовжимо медіану BD так, щоб BD = DK. ?ABD = ?CKD за першою ознакою рівності трикутників, оскільки AB = CD (за умовою), BD = DK (за умовою),∠BDA = ∠CDK (як вертикальні кути).

Із рівності трикутників випливає, що AB = CK, ∠ABK = ∠CKB. Оскільки ∠CKD = ∠ABD = ∠DBC, то? КВС – рівнобедрений, отже, ВС = СК, але СК = АВ, тоді ВС = АВ, тобто? ABC – рівнобедрений.

516.

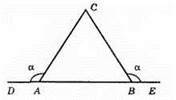
Нехай ∠DAC = ∠EBC = α, тоді ∠CAB = 180° – α, ∠CBA = 180° – α. Оскільки у трикутника ABC два кути рівні, то? ABC – рівнобедрений.

517.

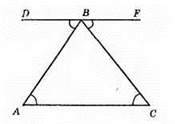
Нехай DF ll АС, ∠DBA = ∠FBC. За властивістю паралельних прямих маємо: ∠A = ∠DBA – як внутрішні різносторонні кути при паралельних прямих DF і АС і січній AB, ∠C = ∠FBC – як внутрішні різносторонні кути при паралельних прямих DF і АС і січній ВС. Звідси ∠A = ∠C. Отже, ?ABC – рівнобедрений.

518.

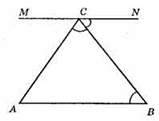
Нехай MN ll AB, ∠NCB = ∠ACB. Оскільки MN ll AB, ∠CNB = ∠ABC – як внутрішні різносторонні кути при паралельних прямих і січеній СВ. Оскільки ∠NCB = ∠ABC, ∠NCB = ∠ACB, то ∠ACB = ∠ABC, тобто? ABC – рівнобедрений.

519.

Нехай в? ABC (AB = ВС), BD ⊥ АС, BD = 1/2AC.

?ABD = ?CBD за першою ознакою рівності трикутників, оскільки AB = ВС (за умовою), BD – спільна сторона, ∠ABD = ∠CBD (бо ∠ABD = 90° – ∠A, ∠CBD = 90° – ∠C, ∠A = ∠C). З рівності трикутників маємо AD = DC.

?ADB, ?CBD – прямокутні рівнобедрені, отже, ∠A = 45°, ∠ABD = 45°, ∠C = 45°, ∠CBD = 45°.

520. Нехай? ABC – рівнобедрений (AB = BC). AD – бісектриса зовнішнього кута FAC. Доведемо, що АD ll ВС.

∠FAD = ∠DAC = α, тоді ∠BAC = 180° – 2α,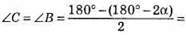

Оскільки ∠DAC = ∠C – як внутрішні різносторонні кути при прямих AD і ВС і січній АС, то AB ll ВС.

521.

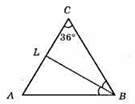
Нехай? ABC – рівнобедрений (АС = СВ), ∠C = 36°, BL – бісектриса кута В.

∠A = ∠B = (180° – 36°) : 2 = 72°. ∠ABL = ∠LBC = 72° : 2 = 36°. Отже, ?CLB – рівнобедрений (CL = LB) з кутами: 36°, 36° і 180° – 72° = 108°.

З? LBA: ∠ALB = 180° – 72° – 36° = 72°. Отже, ?ALB – рівнобедрений з кутами 36°, 72°, 72°.

Відповідь: два трикутники з кутами 36°, 36°, 108°; 36°, 72°, 72°.

522. Оскільки? ABC – рівнобедрений і ∠BAC = 2∠ABC, то знайдемо кути трикутника.

Нехай ∠ABC = х°, тоді ∠BAC = ∠BCA = 2х°. Маємо рівняння: х + 2х + 2х = 180°; 5х = 180°; х = 36°. Отже, кути? АВС дорівнюють: ∠B = 36°, ∠A = ∠C = 72°. Оскільки AB – бісектриса, то ∠BAD= ∠DAC = 72°/2 = 36°. ?ABD – рівнобедрений, тоді BD = AB.

В? ADC ∠DAC = 36°, ∠BCA = 72°, тоді ∠ABC = 180° – 36° – 72° = 72°. Отже, ?ADC – рівнобедрений, тоді AB = АС. Оскільки BD = AB і AB = АС, то BD = АС.

523. Оскілки? АОС – рівнобедрений, то ∠OAC = ∠OCA.

Розглянемо трикутники ABC і CDA. У них АС – спільна, AB = CD (за умовою), ∠BAC = ∠DCA (за доведеним). Отже, ∠ACB = ∠CDA. Із рівності цих трикутників маємо: ∠DAC = ∠BCA, ∠DCA = ∠BAC, AD = ВС.

Оскільки ∠DAC = ∠BCA, ∠DCA = ∠BAC, то ∠DAB = ∠DCB (як різниця рівних кутів ∠DAB = ∠DAC – ∠BAC, ∠DCB = ∠BCA – ∠DCA).

?ADB = ?CBD за першою ознакою рівності трикутників, оскільки AB = CD (за умовою), AD = ВС (за доведеним), ∠DAB = ∠BCD (за доведеним).

524.

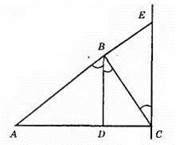
Нехай у трикутнику ABC проведена бісектриса BD (∠ABD = ∠DBC), СЕ || BD. Оскільки СЕ ll BD, то ∠DBC = ∠BCE – як внутрішні різносторонні кути при паралельних прямих і січній ВС. Нехай? ABD = α, тоді ∠DBC = α, ∠BCE = α. ∠ABC – зовнішній кут? ВСЕ, тоді ∠BEC = ∠ABC – ∠BCE = 2α – α = α. Отже, ∠BEC = ∠BCE, тобто? ВСЕ – рівнобедрений.

525.

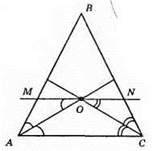
Нехай у? ABC АО і СО – бісектриси, MN ll АС.

∠MOA = ∠OAC – як внутрішні різносторонні кути при паралельних прямих MN і АС і січній АО. Тоді ∠MAO = ∠OAC = ∠MOA.

Отже, ?МОА – рівнобедрений, тоді МО = АМ.

∠NOC = ∠OCA – як внутрішні різносторонні кути при паралельних прямих MN і АС і січній ОС. Тоді ∠NCO = ∠OCA = ∠CON. Отже, ?ONC – рівнобедрений, ON = NC.

Оскільки АМ = MO, ON = NC, TO AM + NC = MO + ON = MN. Отже, AM + NC = MN.

526.

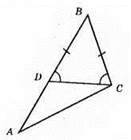
Доведемо, що проти більшої сторони в трикутнику лежить більший кут. Нехай у? ABC AB > ВС, доведемо, що ∠C > ∠A.

Відкладемо на стороні AB від точки В відрізок BD, що дорівнює ВС.

?DBC – рівнобедрений, ∠BDC = ∠BCD – як кути при основі рівнобедреного трикутника DBC. ∠BDC – зовнішній кут трикутника ADC, тому він більший від кута А. Оскільки ∠BCD = ∠BDC, то і кутBCD більший від кута A. ∠BCD > ∠A. Але ∠BCD становить тільки частину кута С, тому ∠C > ∠A.

Доведемо, що проти більшого кута в трикутник лежить більша сторона.

Нехай ∠C > ∠B, доведемо, що АВ > АС.

Можливе одне із трьох співвідношень: 1) АВ = АС; 2) AB < АС; 3) АВ > АС.

Якщо б AB = АС, то ∠C = ∠B, але це суперечить умові. Отже, AB ≠ АС.

Якщо б AB < АС, то ∠C < ∠B, що також суперечить умові.

Отже, можливий тільки один випадок, а саме AB > АС.

Застосуйте на практиці

527. ?ADC = ?ABC за першою ознакою рівності трикутників, оскільки АС – спільна. ВС = DC – за умовою, ∠ACD = ∠ACB = 90°.

Із рівності трикутників випливає, що AB = AD.

528. Щоб провести горизонтальну пряму, досить повернути? АВС так, щоб точка О розмістилася на відрізку ВР.