Коло і круг
Розділ 1. Найпростіші геометричні фігури та їх властивості
§ 15. Коло і круг
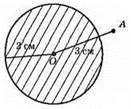
588. 1) Хордами є відрізки: KB, NC, KN, CB, LD.
2) Діаметрами є відрізки: LD, NC, КВ.
3) Радіусами кола є відрізки: OL, OK, ОС, OD, OB, ON.
589. Дотичні до кола: АС, CB, AB. ON ⊥ AC, ОМ ⊥ CB, OK ⊥ AB.
590.
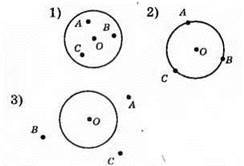
591.
592. Щоб знайти діаметр кола, треба радіус збільшити вдвічі:
1) 6,5 см х 2 = 13 см; 2) 2,6 см х 2 = 5,2 см; 3) m х 2 = 2m см; 4) 2n х 2 = 4n см.
593. Щоб знайти радіус кола, треба діаметр кола поділити пополам:
1) 4,2 : 2 = 2,1 см; 2) 8,2 : 2 = 4,1 см; 3) а
594. З однієї точки можна провести:
1) безліч хорд;
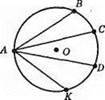
2) один діаметр;
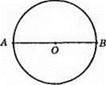
3) один радіус.
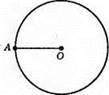
595. Оскільки хорда не може бути більше діаметра, то:
1) Може; 2) може; 3) ні; 4) може.
596.
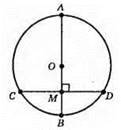
1) АМ не завжди дорівнює ВМ. Рівність досягається, якщо точка М співпадає з центром кола.
2) CM = DM завжди, оскільки? СОМ = ?DOM (за гіпотенузою і катетом: СО = OD – як радіуси кола, ОМ – спільна), то CM = DM.
597.
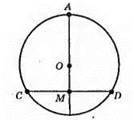
Щоб знайти хорду, треба довжину даного відрізка помножити на
1) 0,5 дм х 2 = 1 дм; 2) 30 мм х 2 = 60 мм; 3) 4,5 см х 2 = 9 см; 4) 0,07 дм х 2 = 0,14 дм.
598.
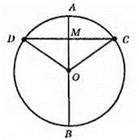
CM = MD, AB – діаметр. Доведемо, що AB ⊥ DC.
?COD – рівнобедрений, отже, OD = ОС, LD = LC.
?OCM = ?ODM за першою ознакою рівності трикутників (OD = ОС, CM = DM, LD = LC). Отже, ∠OMC = ∠OMD = 180°/2 = 90°. AB ⊥ DC.
599. Якщо відрізки рівні і не дорівнюють радіусу кола, то можна стверджувати, що AB ⊥ CD.
1) 2 см = 0,2 дм, отже, AB ⊥ CD;
2) 30 мм ≠ 0,3 см, отже, AB не перпендикулярна CD;
3) 40 см = 4 дм, отже, AB ⊥ CD;
4) 26 см ≠ 0,26 дм, отже, AB не перпендикулярна CD.
600.
1) Перетинаються.
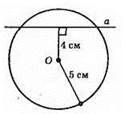
2) Дотикаються.
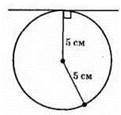
3) Не мають спільних точок.
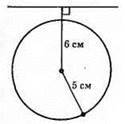
4) Дотикаються.
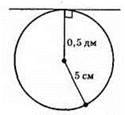
601. 1)
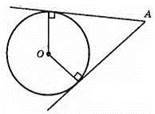
Через дану точку, що лежить поза колом, можна провести дві різні дотичні.
2)
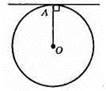
Через дану точку, що лежить на колі, можна провести тільки одну дотичну.
3) Через точку кола, яка лежить всередині кола, дотичну провести не можна.
602. 1) Не мають спільних точок (R = 10 см, r = 5 см).
ОО1 = 16 см.
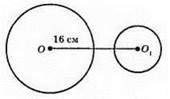
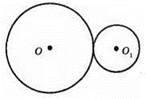
2) Дотикаються зовні (R = 8 см, r = 6 см).
ОО1 = 14 см.
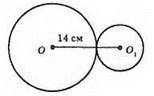
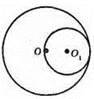
3) Дотикаються внутрішньо (R = 16 см, r = 12 см).
ОО1 = 4 см.
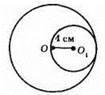
603. a)
Якщо R = 6 см, r = 4 см, то ОО1 = R + r = 6 см + 4 см = 10 см.
Б) ОО1 = 6 см – 4 см = 2 см.
Відповідь: 10 см, 2 см.
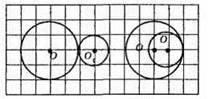
604. Кола 1 і 2, 1 і 3, 1 i 4, 1 і 5 дотикаються (внутрішній дотик).
Кола 2 і 3, 3 і 4, 4 і 5, 5 і 2 перетинаються.
Мал. 345.
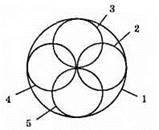
Кола 2 і 4, 3 і 5 дотикаються (зовнішній дотик).
Мал. 346.
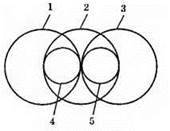
Кола 1 і 2, 2 і 3 перетинаються.
Кола 2 і 5, 2 і 4 мають внутрішній дотик.
Кола 1 і 3, 5 і 4 мають зовнішній дотик.
605. 1) Всередині круга.
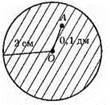
2) На колі.
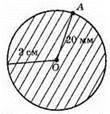
3) Всередині круга.
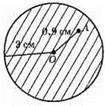
4) Поза кругом.
606. Не можуть.
607.
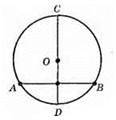
Якщо АВ – діаметр, то AB = CD. Якщо AB – не діаметр, то CD > АВ.
608. ОК ⊥ АВ, ОК = 10 см.
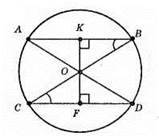
Оскільки? КОВ = ?FOC (∠B = ∠C – внутрішні різносторонні кути при паралельних прямих AB і CD і січній ВС, BO = СО, ∠OKB = ∠OFC = 90°), то OK = OF. Отже, OF = 10 см.
609.
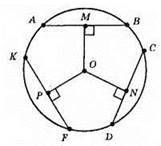
Оскільки AB = CD = KF, ОМ ⊥ AB, ON ⊥ CD, OP ⊥ KF, TO MO = ON = OP = 6 см.
610.
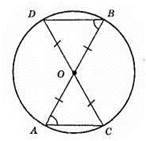
?AOC = ?BOD (оскільки AO = BO, CO = DO, ∠AOC = ∠BOD), TO AC = BD і ∠OAC = ∠OBD.
Оскільки кути OAC і OBC – внутрішні різносторонні при прямих DB і АС та січній AB і рівні, то АС || ВН.
611.
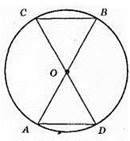
AD = 3 CM, CD = 8 CM.
P? ABC = OC + BC + OB = (OC + OB) + BC = AB + BC. Оскільки AB = CD, BC = AD, то Р? ABC = AD + CD = 3 CM + 8 CM = 11 CM.
Відповідь: 11 CM.
612.
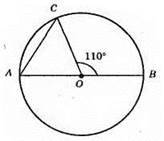
?АОС = 180° – 110° = 70°. ?АОС – рівнобедрений, отже,
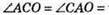
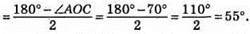
Відповідь: 55°.
613.
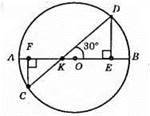
СК = 6 CM, DK = 12 см. CF ⊥ AB, DE ⊥ AB, ∠DKE = 30°.
З прямокутного трикутника KDE: DE = 1/2 DK = 1/2 • 12 = 6 (см).
З прямокутного? FKC: FC = 1/2CK = 1/2 • 6 = 3 (CM).
Відповідь: 6 см, 3 см.
614.
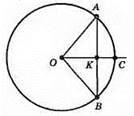
ОС ⊥ АВ, ОК = СК.
З прямокутного? АОК маємо: ∠ОАК = 30° (оскільки АО = 2ОК).
З прямокутного? ВОК маємо: ∠ОВК = 30° (оскільки OB = 2OK).
З? АОВ: ∠AOB = 180° – ∠ОАК – ∠ОВК = 180° – 30° – 30° = 120°.
Відповідь: 120°.
615. Ні. Оскільки дотична перпендикулярна до радіуса, проведеного в точку дотику, то припустивши, що коло дотикається до прямої в двох точках, отримаємо, що з центра кола до прямої можна провести два перпендикуляри, що неможливо.
616.
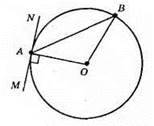
1) Якщо ∠АОВ = 70°, то
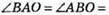
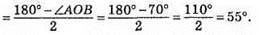
Тоді ∠NAB = 90° – 55° = 35°.
2) Якщо AB = АО, то? АОВ – рівносторонній і ∠ВАО = 60°. Тоді ∠NAB = 90° – 60° = 30°.
617.
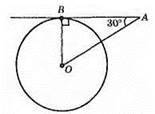
Відповідь: 1) 35°; 2) 30°.
Оскільки OB ⊥ AB, ∠ВАО = 30°, АО = 8 см, то ВО = 1/2AО = 1/2 • 8 = 4 (см).
Відповідь: 4 см.
618.
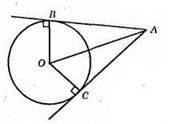
Оскільки В і С – точки дотику, то OB ⊥ AB, ОС ⊥ АС. ?АBО = ?АСО (за катетом і гіпотенузою: OB = ОС – як радіуси, ОА – спільна гіпотенуза), тоді АB = АС.
619.
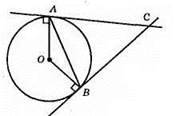
Згідно з результатами задачі 318: АС = BС. За умовою АB = АС, отже, ?ABC – рівносторонній і ∠CAB = ∠ABC = ∠BCA = 60°.
Відповідь: 60°, 60°, 60°.
620.
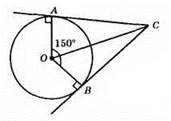
?АОС = ?ВОС (за гіпотенузою ОС і катетом AO = OB).
∠AOC = 1/2∠AOB = 1/2 • 150° = 75°. ∠ACO = ∠BCO = 90° – 75° = 15°.
Тоді ∠ACB = ∠ACO + ∠BCO = 15° + 15° = 30°.
Відповідь: 30°.
621.
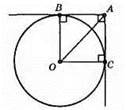
?BАО = ?САО (за гіпотенузою і катетом: ОА – спільна, ОB = ОС).
∠BAO = ∠CAO = 90°/2 = 45°, тоді ∠BOA = ∠COA = 90° – 45° = 45°. Оскільки? ОBА і? ОСА – рівнобедрені, то АB = OB = R, АС = ОС = R. Отже, AB = АС = R.
Відповідь: AB = АС = R.
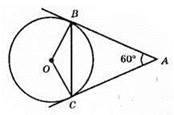
622.
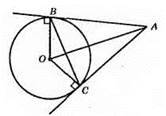
1) Оскільки? ABC – рівнобедрений (AB = АС) і ∠BAC = 60°, то? ABC – рівносторонній. Отже, ВС = АВ = АС.
2) Оскільки? ОВА = ?ОСА, то ∠OAB = ∠OAC = 30°. Із прямокутного трикутника ABO (∠B = 90°, ∠A = 30°) маємо: ОА = 2 х OB, тобто відрізок ОА дорівнює діаметру.
623.
1) Оскільки AB = ВС = АС (задача 622), і якщо AB = 4 см, то ВС = 4 см.
2) Оскільки AB = ВС = АС (задача 622), то якщо AB + АС = 10 см, АВ = АС = 10/2 = 5 (см). Отже, ВС = АB = АС = 5 см.
Відповідь: 1) 4 см; 2) 5 см.
624.
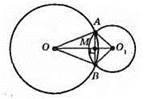
1) ?AOO1 = ?BOO1 за трьома сторонами (ОА = OB – як радіуси, O1A1 = O1В1 – як радіуси, OO1 – спільна сторона).
Із рівності цих трикутників маємо: ∠AOO1 = ∠BOO1.
2) ?ОАВ – рівнобедрений, тоді кути при основі рівні, тобто ∠OAB = ∠OBA.
3) Оскільки? ОАВ – рівнобедрений і ОМ – його бісектриса (∠AOO1 = ∠BOO1), то ОМ – медіана і висота, отже, ОО1⊥ АВ.
625.
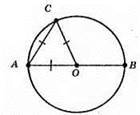
Оскільки АС = AO = СО, то? АОС – рівносторонній. Отже, ∠CAO = 60°.
Відповідь: 60°.
626.
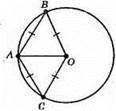
Оскільки AB = BO = АО = АС = СО, то? АВО і? АСО – рівносторонні. Отже, ∠BAO = 60°, ∠CAO = 60°. Тоді ∠BAC = ∠BAO + ∠CAO = 60° + 60° = 120°.
Відповідь: 120°.
627.
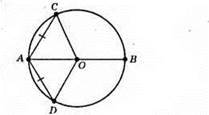
Hexай AB – діаметр, АС = AB. Доведемо, що ∠CAO = ∠DAO.
?САО = ?DAO за трьома сторонами (СО = DО – як радіуси, АС = AD – за умовою, АО – спільна сторона). Із рівності цих трикутників випливає, що ∠CAO = ∠DAO.
628.
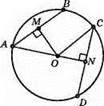
Нехай AB = CD, ОМ ⊥ AB, ON ⊥ CD. Доведемо, що ОМ = ON.
Оскільки ОМ ⊥ AB, то AM = MB. Оскільки ON ⊥ CD, то CN = ND.
?OMA = ?ONC за гіпотенузою і катетом (ОА = ОС – як радіуси, AM = CN – як половини рівних хорд), тоді ОМ = ON.
629.
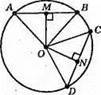
Якщо хорди рівновіддалені від центра кола, то вони рівні.
Нехай ОМ ⊥ AB, ON ⊥ CD, ОМ = ON. Доведемо, що AB = CD.
Оскільки ОМ ⊥ AB, ON ⊥ CD, то AM = MB, CN = ND.
?AOM = ?CON за гіпотенузою і катетом (АО = СО – як радіуси, ОМ = ON – за умовою), тоді AM = CN. Отже, AB = 2AM = 2CN = CD.
630.
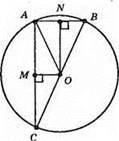
ОМ ⊥ AC, ОМ = 10 CM, ON ⊥ AB, ON = 30 CM, ?AMO = ?ONA за гіпотенузою і гострим кутом). Із рівності трикутників випливає, що AM = ON, MO = AN. Тоді АС = 2 х ON = 2 х 30 CM = 60 см, AB = 2 x ОМ = 2 х 10 см = 20 см.
Відповідь: 60 см, 20 см.
631.
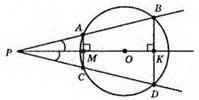
РО – бісектриса кута. ∠BPO = ∠DPO. Доведемо, що AB = CD.
BD ⊥ PO, АС ⊥ PO. ?PBK = ?PDK (за катетом і гострим кутом: РК – спільний катет, ∠BPK = ∠DPK), тоді PB = PD.
?РАМ = ?РСМ (за катетом і гострим кутом: РМ – спільний катет, ∠АРМ = ∠СРМ), тоді PA = PC.
Отже, AB = PB – PA, CD = PD – PC. Оскільки РВ = PD, PA = PC, то AB = CD.
632. Оскільки AB ll CD, то ∠ANM + ∠CMN = 180° (як сума внутрішніх односторонніх кутів при паралельних прямих і січній MN). NO – бісектриса кута ANM, МО – бісектриса кута CMN, тоді
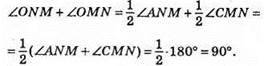
633.
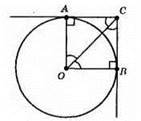
Оскільки? АСВ – ?АОВ і? АОС = ?ВОС, то
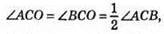
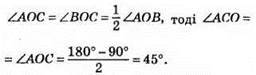
Тоді ∠АОВ = 2 х ∠АОС = 2 x 45° = 90°.
Відповідь: 90°.
634.
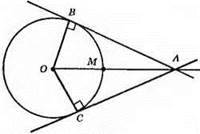
OB ⊥ AB, ОС ⊥ АС, AM = МО.
?ОВА = ?ОСА, тоді ∠ВАО = ∠САО.
Із? ОВА (∠В = 90°, ОА = 2OВ) випливає, що ∠ВАО = 30°, тоді ∠ВАС = 2 х ∠ВАО = 2 х 30° = 60°.
Відповідь: 60°.
