Комбінації тіл
1073.
Нехай ABCDA1B1C1D1 – куб, вписаний в кулю з центром О,
B1O = OD = 8 см. Тоді B1D = 2В1О = 2 × 8 = 16 (см).
Відповідь: 16 см.
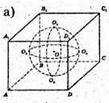
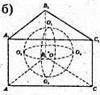
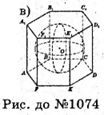
1074.
Див. рис.
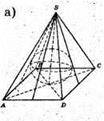
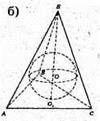
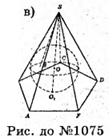
1075.
Див. рис.
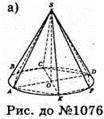
1076.
Див. рис.
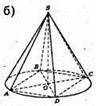
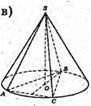
1077.
Див. рис.
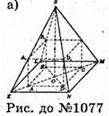
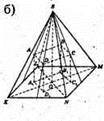
1078.
Див. рис.
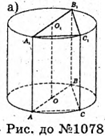
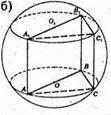
1079.
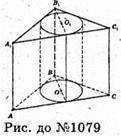
Нехай ABCA1B1C1 – правильна трикутна призма. Sбіч. = 27 см2.
Нехай AB = а, тоді 3а × AA1= 27, звідси а × AA1 = 9.
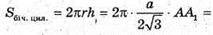
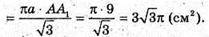
Відповідь: 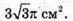
1080.
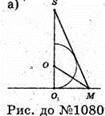
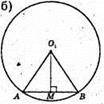
Нехай SM – апофема правильної n-кутної піраміди,
O1M – проекція апофеми правильної n-кутної піраміди
На основу піраміди. ∠SMO1 = α,
Тоді 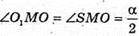 і O – центр кулі, вписаної в n-кутну піраміду.
і O – центр кулі, вписаної в n-кутну піраміду.
Нехай AB – сторона правильного n-кутника, AB = а.
Тоді зі ΔАО1М: 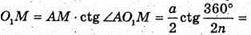
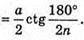
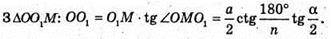
Відповідь: 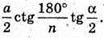
1081.
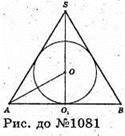
Нехай в конус (Δ SAB – осьовий переріз конуса) вписано кулю
З центром в точці О, OO1 + АВ, OO1 = r, ∠SAO1 = α.
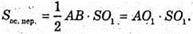
Із ΔAOO1: 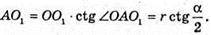
Із ΔSAO1: 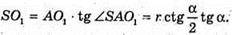
Тоді 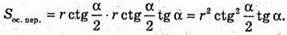
Якщо r = 2 м, α = 50°, то
S ос. пер.= 22 × сtg225° × tg 50° = 4 × (2,1445)2 × 1,1918 = 22 (м2)
Відповідь: 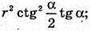 ≈ 22 м2.
≈ 22 м2.
1082.
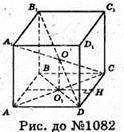
Нехай у прямому паралелепіпеді ABCDA1B1C1D1,
У якого A1C = 6 см, B1D = 8 см, вписано кулю з центром в точці О.
ABCD – ромб, висота якого дорівнює діаметру кулі,
Або висоті паралелепіпеда. Нехай АA1 = 2x,
Тоді із ΔAA1C: 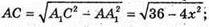
Iз ΔBB1D: 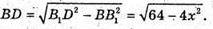
Із ΔAO1D: 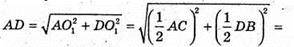
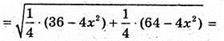
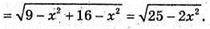
Оскільки 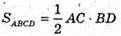 і
і 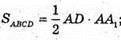
То 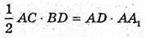 або
або
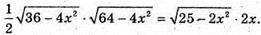
(36 – 4х2)(64 – 4х2) = (25 – 2х2) × 16х2·,
4 × 4(9 – x2)(16 – x2) = (25 – 2×2) × 16×2; (9 – x2)(16 × x2) = x2(25 – 2×2);
144 – 9×2 – 16×2 + x4 = 25×2× 2×4; 3×4- 50×2 + 144 = 0;

Якщо 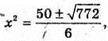 то
то 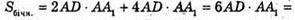
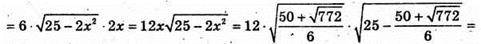
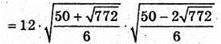 – не задовольняє умову, бо
– не задовольняє умову, бо 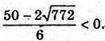
Якщо 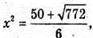 то
то 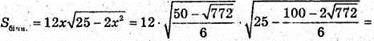
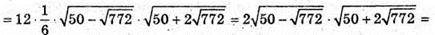
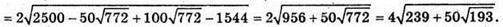
Відповідь: 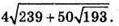
1083.
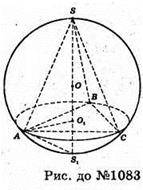
Нехай SABC – правильна трикутна піраміда AS = 12 см, ∠SAO1 = 60°,
SO1+ (ABC). O – центр кулі, описаної навколо піраміди.
Проведемо промінь SO до перетину з поверхнею кулі в точці S1.
Тоді ΔSAS1- прямокутний, у якого AS = 12 см і
∠ ASS1= 90° – ∠SAO1 – 90° – 60° = 30°.
Із ΔSAS1: 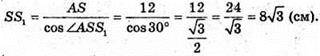
Тоді 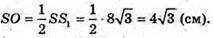
Відповідь: 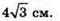
1084.
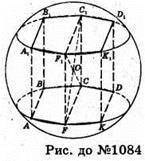
Нехай правильна шестикутна призма ABCDKFA1B1C1D1K1F1 вписана в кулю з центром О. AA1 = 12 см, OC = 10 см.
Iз ΔFF1C:
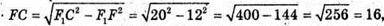
Тоді 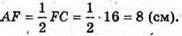
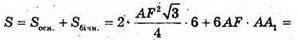
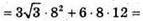
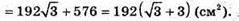
Відповідь: 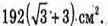
1085.
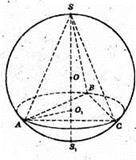
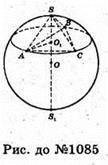
Нехай SABC – правильна трикутна піраміда, вписана в кулю з центром О,
OA = OB = OC = OS = 13 см. SO1- висота піраміди OO1 = 5 см.
Проведемо промінь SO до перетину з поверхнею кулі в точці S1.
І випадок (точка O лежить між точками S і O1).
SO1 = SO + OO1= 13 + 5 = = 18 (см),
SS1 = 2SO = 2 × 13 = 26 (см).
Тоді із прямокутного трикутника SAS1:
AS2= SO1× SS1 = 18 × 26 = 468;
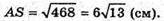
II випадок (точка O лежить між точками S і О).
SO1 = SO – OO1 = 13 – 5 = 8 (см).
SS 1 = 2SO = 2 × 13 = 26 (см).
Тоді із прямокутного трикутника SAS 1:
AS2 = SO 1 × SS1 = 8 × 26 = 208;
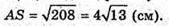
Відповідь: 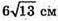 і
і 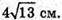
1086.
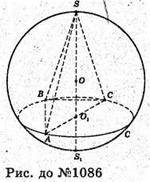
SABC – трикутна піраміда, в якій ∠ ABC = 90°, AB = 12 см, BC = 16 см,
SO1+ (ABC). Оскільки ΔABC – прямокутний, то O1- центр кола,
Описаного навколо трикутника ABC:
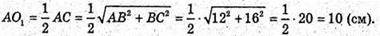
Оскільки піраміда SABC вписана в кулю з центром О, то продовживши промінь SO до перетину його з поверхнею кулі в т. S1маємо:
AO1 = SO1 × O1S; 102 = SO1× (SS1 – SO1);
100 = SO1(20 – SO1); SO 1 – 20 × SO1 +100 = 0; SO1 = 10 см.
Далі із ΔASO1: 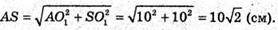
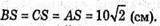
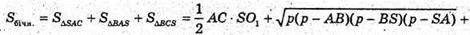
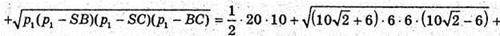
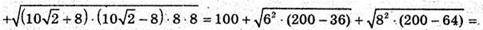

Відповідь: 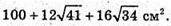
1087.
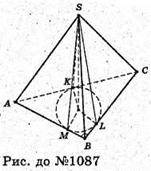
SABC – піраміда, ∠ABC = 90°, AB = 10 м, BC = 24 м, SO + (ABC).
K, L, M – точки дотику вписаного в основу піраміди кола:
∠SLO = ∠SMO = ∠SKO = 60°.
Із ΔABC: 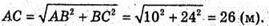
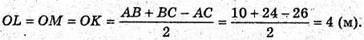
Із Δ SOL: 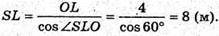
Sкон. = Sбічн.+Socн. = π × OL × SL+π × OL2 = π×4×8+ π×42 = 32π+16π = 48π (см2).
Відповідь: 48π см2.
1088.
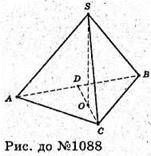
SABC – трикутна піраміда, AC = SC, AB = a, ∠BAC = α; ∠ABC = α. SO + (ABC).
Оскільки усі бічні ребра утворюють з площиною основи рівні кути, то O – центр кола, описаного навколо трикутника ABC: ∠SAO = ∠SBO = ∠SCO = β.
За теоремою синусів із трикутника ABC маємо: 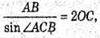
Тоді 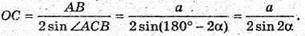
Із Δ SOC: 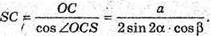
Тоді площа S бічної поверхні конуса, описаного навколо піраміди,
Дорівнює π × OC × SC.
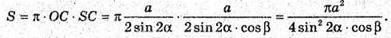
Відповідь: 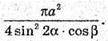
1089.
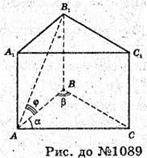
ABCA1B1C1 – пряма трикутна призма, AB = с, ∠CAB = α, ∠ABC = β, ∠B1AB = φ.
За теоремою синусів із трикутника ABC маємо: 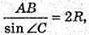
Тоді 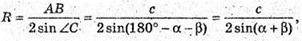
Де R – радіус кола, описаного навколо трикутника ABC;
Радіус основи циліндра, описаного навколо призми.
Із ΔABB1: BB = AB × tg ∠ B1AB = с tg φ.
Тоді 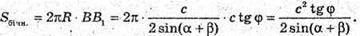
Відповідь: 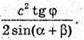
1090.
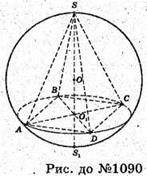
SABCD – правильна чотирикутна піраміда, SO1 + (ABC).
SO = AO = BO = CO = DO = r. ∠SAO1 = ∠SBO1 = ∠SCO1= ∠SDO1 = α.
Проведемо промінь SO до перетину його з сферою в точці S1.
Із прямокутного трикутника SAS1маємо
AS = SS1× cos ∠ASS1 = 2r × cos(90° – α) = 2r sin α.
Із ΔАSS1: AS2 = SO 1 × SS1, тоді
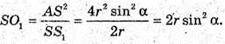
Відповідь: 2r sin2а.
1091.
A)
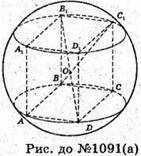
ABCDA1B1C1D1- прямокутний паралелепіпед, у якого AB = a, AD = b, AA1= с.
O – центр кулі, описаної навколо прямокутного паралелепіпеда.
Оскільки OA = OB = OC = OD = OA1 = OB1= OC1= OD1, то O – точка перетину діагоналей паралелепіпеда, а довжина діагоналі дорівнює діаметру кулі.
Тоді 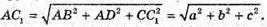
Відповідь: 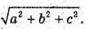
Б)
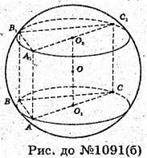
ABCA1B1C1-· пряма призма, AA1 = с, ∠ABC = 90°, AB = a, BC = b.
Оскільки ΔABC – прямокутний, то AC – діаметр кола, описаного навколо трикутника ABC.
Оскільки ΔA1B1C1 – прямокутний, то A1C1- діаметр кола, описаного навколо трикутника A1B1C1.
O – центр сфери, описаної навколо прямої призми.
Із ΔАВС: 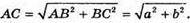
Із ΔACC1: 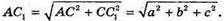
Відповідь: 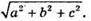
В)
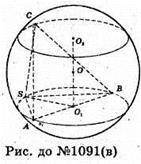
SABC – піраміда, в якій SA + SB, SA + SC, SB + SC, SA = a, SB = b, SC = с.
O1- центр кола, описаного навколо трикутника SAB. Проведемо переріз сфери площиною, яка проходить через точку C і паралельна площині (SAB).
О2 – центр перерізу.
Тоді точка O – центр кулі є серединою відрізка O1O2, тоді
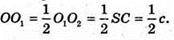
Із ΔASB маємо: 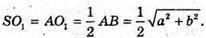
Із ASOO1: 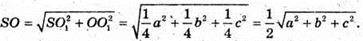
Оскільки 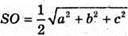 – радіус кулі, то її діаметр дорівнює
– радіус кулі, то її діаметр дорівнює 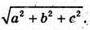
Відповідь: 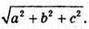
1092.
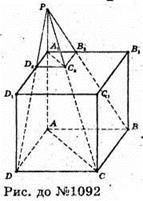
Нехай ABCDA1B1CiD1- куб, AB = а. За умовою PA = 2а. ΔPAD = ΔРАB,
Тоді ΔPAD – ΔPA1D2.
Звідси 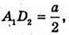
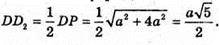
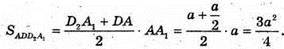
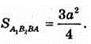
ΔPA1C2- ΔРАС, тоді 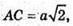
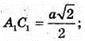
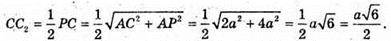
ΔPDC = ΔPBC, ΔPD2C2 = ΔPB2C2, тоді
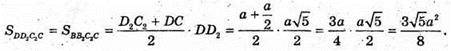
Тоді 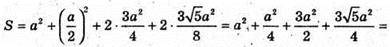
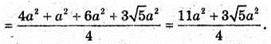
Відповідь: 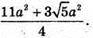
1093.
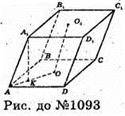
Нехай ABCDA1B1C1D1- похила призма, в якій AA1 = BB1 = CC1 = DD1= 12 см.
Нехай O і O1- точки дотику сфери, вписаної в похилу призму, з основами призми, тоді O1O = 2 × 3 = 6 (см) і OO1- висота призми.
Провівши A1K? OO1із ΔAA1K, маємо: 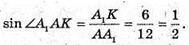
Отже, 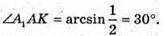
Отже, бічне ребро нахилене до площини основи під кутом 30°.
Відповідь: 30°.
1094.
А)
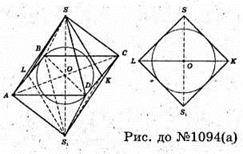
Нехай SABCDS1- правильний октаедр, AB = а.
Розглянемо переріз правильного октаедра площиною, яка проходить через точки S, S1і K – середина ребра DC. SKS1L – переріз – ромб,, оскільки
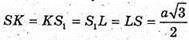
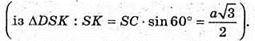
Радіус вписаної в октаедр кулі дорівнює радіусу круга, вписаного в ромб SKS1L, тобто половині висоти ромба.
Із ΔSOK маємо: 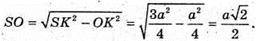
Оскільки 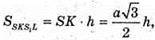
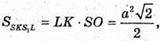
Тоді 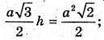
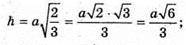
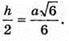
Відповідь: 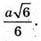
Б)
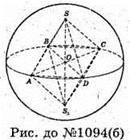
Нехай SABCDS1- правильний октаедр, AB = а. Радіус кулі, описаної навколо правильного октаедра, дорівнює довжині відрізка SO.
Із ΔSOC: SO2 + OC2 = SC2; 2SO2 = SC2; 2SO2= а2;
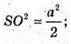
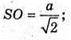
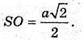
Відповідь: 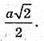
В)
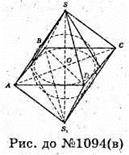
Нехай SABCDS1- правильний октаедр, AB = а.
Радіус кулі, яка дотикається до всіх ребер даного октаедра, дорівнює радіусу круга, вписаного в квадрат ABCD, тобто 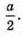
Відповідь: 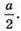
1095.
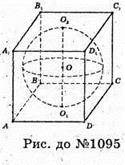
Нехай в призму ABCDA1B1C1D1вписано кулю з центром О; O1і O2 – точки дотику кулі до основ призми. O1O2 = 2r. Периметр основи призми дорівнює Р.
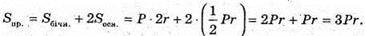
Відповідь: 3Pr.
1096.
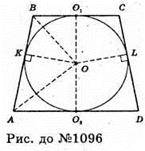
Нехай ABCD – осьовий переріз зрізаного конуса; а круг, вписаний в трапецію ABCD, – переріз кулі, вписаної в зрізаний конус. AO2 = R, BO1= r.
Нехай OK + AB, OL + CD, тоді KB = BO1, O1C = CL і AK = AO2, DO2 = DL.
Тоді ∠AOB = 90° (оскільки BO і AO – бісектриси кутів. O1BK і KAO2і
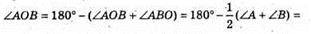
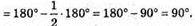
Із ΔAOB: 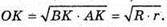
Відповідь: 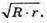
1097.
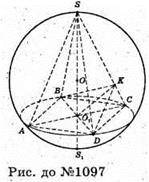
SABCD – правильна піраміда, яка вписана в кулю з центром О. Нехай SO = 4х,
OO1 = 3х. S1- точка перетину променя SO з поверхнею кулі, тоді
S1O1 = OS1- OO1 = 4x – 3х = х.
Із прямокутного трикутника SAS1:
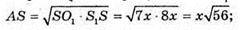
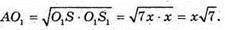
Тоді 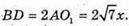
Проведемо KB + SC, KD + SC.
Із ΔSCD: SM × CD = DK × SC (SM + CD), тоді
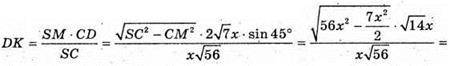
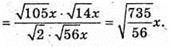
Із Δ BKD: BK2 + DK2- 2BK × KD cos φ = BD2;
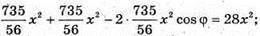
735 + 735 – 2 × 735 cos φ = 28 × 56;
1470 -1578 = 1470 cos φ;
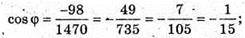
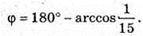
Відповідь: 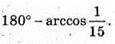
1098.
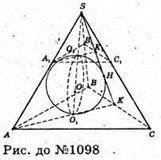
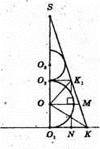
Нехай в правильний тетраедр вписана сфера з центром в точці О, тоді
O1O2 = 2R. Нехай AB = х, тоді 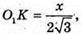
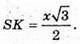
Враховуючи, що 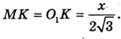
Оскільки ΔSOM – ΔSKO1, то 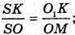
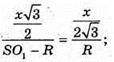
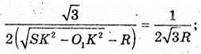
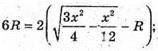
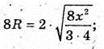
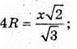
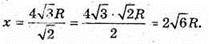
SA1B1C1 – правильний тетраедр, тоді радіус кулi вписаної в цей тетраедр, дорівнює 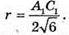
Знайдемо A1C1. Оскільки ΔSO1K – ΔSO2K, то 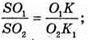
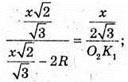
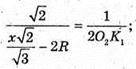
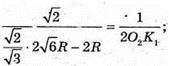
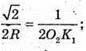
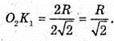 Оскільки
Оскільки 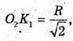
То 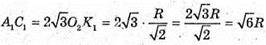
І тоді 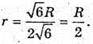
Відповідь: 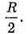
1099.
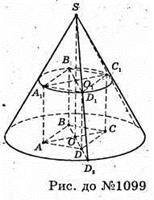
Нехай ребро кубаABCDA1B1C1D1, вписаного в конус, дорівнює x, тоді
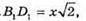
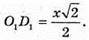
ΔSOD2- ΔSO1H1, тоді 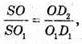 звідси
звідси 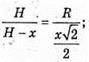
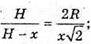
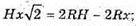
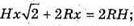
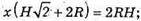
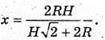
Відповідь: 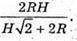
1100.
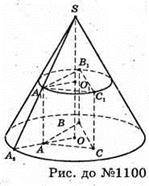
Нехай призма ABCA1ByC1вписана в конус. 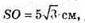 A2O = 10 см, причому
A2O = 10 см, причому
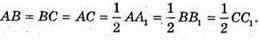
Нехай AB = х, тоді AA1 = 2х.
ΔA2SO – ΔA1SO1, тоді 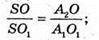
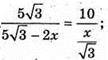
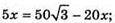
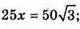
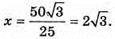
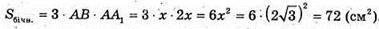
Відповідь: 72 см2.
1101.
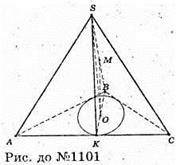
SABC – правильна піраміда, SO + (ABC), BK + АС, тоді SK + AC (за теоремою про три перпендикуляри), ∠SKO = α, M – середина SB, OM = m; оскільки ΔSOB – прямокутний і OM – медіана, то SB = 2OM = 2m.
Нехай OK = х, тоді OB = 2х; 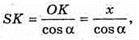
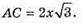
Із ΔASK: AS2 = АК2 + SK2, 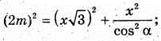
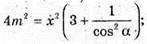
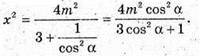
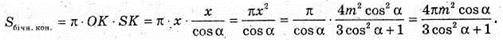
Відповідь: 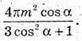
1102.
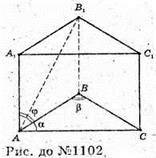
Нехай ABCA1B1C1- пряма призма, в якій AB = с, ∠A = a, ∠B = β. ∠B1AB = φ.
Із ΔАВС: 
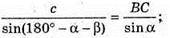
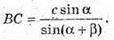
Із ΔABC: 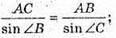
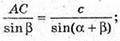
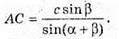
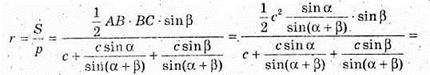
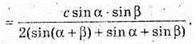
Із ΔABB1: BB1= AB × tg φ = ctg φ.
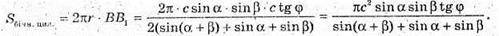
Відповідь: 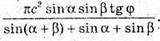
1103.
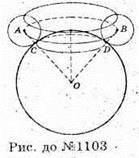
ΔОАВ – ΔOCD, тоді 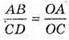 або
або 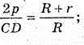
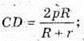
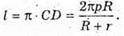
Відповідь: 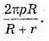
1104.
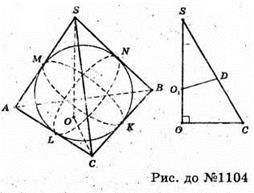
Нехай SABC – правильний тетраедр, SA = SB = SC = AB = BC = AC = а.
Центр кулі, яка дотикається трьох ребер правильного тетраедра, які виходять з однієї вершини, повинен лежати на бісектрисі відповідного трьохгранного кута, яка збігається з висoтою тетраедра, проведеної з цієї ж вершини. Оскільки всі чотири бісектриси перетинаються в одній точці – центрі вписаної в тетраедр кулі. Тому досить розглянути трикутник SOC, де SO – висота тетраедра, SC – його ребро, SC = а, O – центр шуканої кулі і кулі, вписаної в тетраедр.
ΔSOA – ΔSDO1, тоді 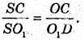
Оскільки SC = а, 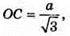
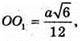
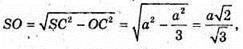
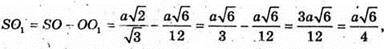
То 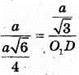 звідси
звідси 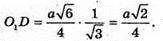
Відповідь: 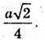
1105.
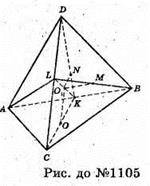
DABC — тетраедр, AB = CD = 6, 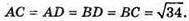
Нехай K i L – середини ребер AB і CD. Оскільки трикутники ADB і ACB – рівнобедрені, то CK + AB і DK + AB. Отже, кут DKC – лінійний кут двогранного кута з ребром АВ. Із прямокутних трикутників ADK і ACK знаходимо
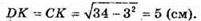
ΔDKC – рівнобедрений, тому KL – бісектриса кута CKD. Тоді півплощина ALB (з межею АВ) – бісектор двогранного кута з ребром АВ.
Аналогічно встановлюємо, що CDK – півплощина (з межею CD) є бісектором двогранного кута з ребром CD. Центр кулі, вписаної в тетраедр, лежить на відрізку KL – перетині цих бісекторів. 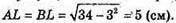
Із прямокутного трикутника LKB: 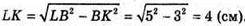
Нехай О1 – центр вписаної кулі, r – її радіус. Проведемо перпендикуляри OM і ON до граней DBA і DBC, тоді ON = OM = г. Позначимо ще ∠BLK = α, ∠DKL = β.
Із прямокутних трикутників BLK і DKL знаходимо 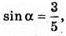
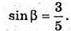
Із прямокутного трикутника O1ML маємо 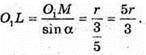
Тоді 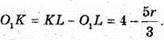
Тоді із прямокутного трикутника O1NK одержуємо рівняння
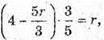 тоді
тоді 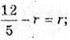
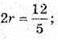
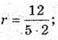
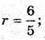 r = 1,2.
r = 1,2.
Відповідь: 1,2.
1106.
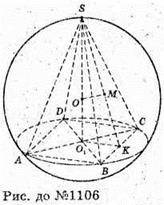
Нехай SABCD – правильна чотирикутна піраміда,
В якій AB = BC = CD = AD = 2а. O – центр вписаної і описаної куль.
Нехай SK + ВС, ∠O1KS = 2α. Тоді SO1 = a tg 2α; OO1 = a tg α;
OB = SO1 = OO1 = a tg 2α – а tg α. 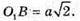
Із прямокутного трикутника OO1B: OB 2 = OO1 +O1B
(a tg 2α – а tg α)2 – a2 tg2α + 2а2; tg22α – 2 tg α tg 2α + tg2 α = tg2 α + 2;
Tg22α – 2 tg 2а × tg α – 2 = 0;
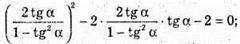 4 tg2 α – 4 tg2α(1 – Ig2α) – 2(1 – tg2α)2 = 0;
4 tg2 α – 4 tg2α(1 – Ig2α) – 2(1 – tg2α)2 = 0;
4 tg2α – 4 tg2α + 4 tg2α – 2 + 4 tg2α – 2 tg4α = 0; 2 tg4 α + 4 tg2α – 2 = 0;
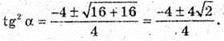
Оскільки 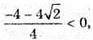 то
то 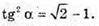
Оскільки tg α > 0, то 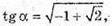
Тоді 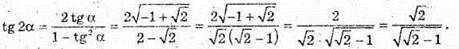
Оскільки 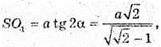
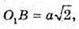
Тоді 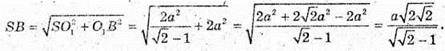
Далі із Δ SBC: SB2 + SC2- 2SB × SC × cos φ = BC2;
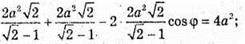
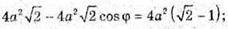
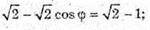
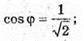
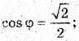 φ = 45°.
φ = 45°.
Відповідь: 45°.
1108.
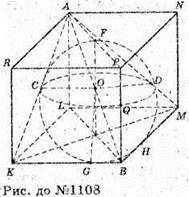
Нехай ребро куба дорівнює a, AB – його діагональ. O – центр кулі, яка дотикається до граней KLAR, LMNA, RANP, тоді CO = OD = OF = r
І 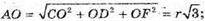
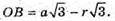
Оскільки куля дотикається до ребер KB, BM і BP в точках G, H і Q, то
OG = OH = OQ = r. В ΔOGB: OG = r, GB = а – r, 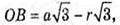
Тоді маємо: OB2= OG2 + GB2; 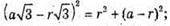
3a2- 6аr + 3r2 = r2 + а2 – 2аr + r2; r2 – 4аr + 2а2 = 0;
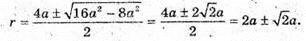
Оскільки 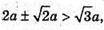 то це значення r умову задачі не задовольняє.
то це значення r умову задачі не задовольняє.
Отже, 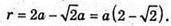
Відповідь: 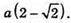
1109.
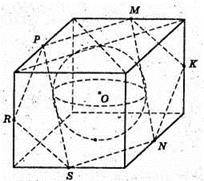
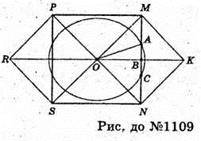
Розглянемо переріз куба площиною, яка проходить через, точки М, N, K – середини ребер куба.
Нехай ребро куба дорівнює а, тоді 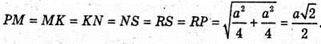
Радіус вписаної кулі в куб дорівнює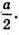 Тоді
Тоді 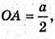
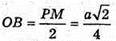
І із прямокутного трикутника OAB: 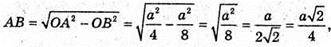
Тоді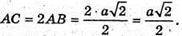
Відповідь: