Головна ⇒ 📌Довідник з геометрії ⇒ Кут між мимобіжними прямими
Кут між мимобіжними прямими
Геометрія
Стереометрія
Кут між мимобіжними прямими
Дві прямі, що перетинаються, утворюють суміжні та вертикальні кути. Кутова міра меншого із суміжних кутів називається Кутом між прямими. Кут між перпендикулярними прямими дорівнює 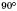 за означенням.
за означенням.
Кут між паралельними прямими вважаємо таким, що дорівнює нулю.
Кутом між мимобіжними прямими називається кут між прямими, які перетинаються й паралельні даним мимобіжним прямим. Цей кут не залежить від вибору прямих, що перетинаються.
Мимобіжні
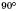 , теж називаються Перпендикулярними.
, теж називаються Перпендикулярними.Отже, якщо пряма перпендикулярна до площини, то вона перпендикулярна до будь-якої прямої на цій площині.
Теорема. Будь-яка пряма на площині перпендикулярна до проекції похилої на цю площину тоді й тільки тоді, коли ця пряма перпендикулярна до самої похилої. (У такому вигляді часто використовують теорему про три перпендикуляри.)
Приклади
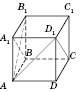
1) На рисунку ABCDA1B1C1D1 – куб.
а) Кут між
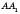 і DС –
і DС – 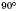 ;
;б) кут між
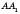
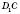 –
– 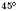
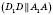 ;
;в) кут між
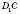 і
і 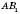 –
– 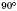 ;
;г) кут між
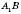 і
і 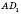 –
– 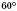 (
(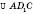 – рівносторонній).
– рівносторонній).
2) На рисунку ABCD – ромб. Пряма MO перпендикулярна до його площини:
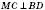 .
.



 (1 votes, average: 5.00 out of 5)
(1 votes, average: 5.00 out of 5)Related posts:
- Кут між мимобіжними прямими Урок 53 Тема. Кут між мимобіжними прямими Мета уроку: формування поняття кута між мимобіжними прямими, а також вмінь учнів знаходити кути між мимобіжними прямими. Обладнання: стереометричний набір, моделі куба, тетраедра, прямокутного паралелепіпеда. Хід уроку II. Перевірка домашнього завдання В кінці уроку збираються учнівські зошити для перевірки їх ведення і виконання домашнього завдання. III. Сприйняття й […]...
- Розв’язування задач на знаходження відстані між мимобіжними прямими Урок 41 Тема. Розв’язування задач на знаходження відстані між мимобіжними прямими Мета уроку: формування вмінь учнів у знаходженні відстані між двома мимобіжними прямими. Обладнання: стереометричний набір, моделі куба і прямокутного паралелепіпеда. Хід уроку 1. Фронтальна бесіда за контрольними запитаннями № 13-15 та перевірка правильності розв’язання домашньої задачі. 2. Математичний диктант. Дано зображення куба: варіант 1 […]...
- Відстань між мимобіжними прямими Урок 40 Тема. Відстань між мимобіжними прямими Мета уроку: формування понять спільного перпендикуляра, відстані між мимобіжними прямими. Обладнання: стереометричний набір. Хід уроку 1. Фронтальне опитування. 1) Які дві площини називаються перпендикулярними? 2) Сформулюйте ознаку перпендикулярності площин. 3) Як розташована пряма, яка лежить в одній із двох перпендикулярних площин і перпендикулярна до лінії перетину цих площин, […]...
- Відстань між мимобіжними прямими Геометрія Стереометрія Відстань між мимобіжними прямими Спільним перпендикуляром до двох мимобіжних прямих називається відрізок із кінцями на цих прямих, перпендикулярний до кожної з них. Теорема. Дві мимобіжні прямі мають спільний перпендикуляр, і до того ж тільки один. Він є спільним перпендикуляром до паралельних площин, які проходять через ці прямі. Відстанню між мимобіжними прямими називається довжина […]...
- Перпендикулярність прямих і площин Геометрія Стереометрія Перпендикулярність прямих і площин Дві прямі називаються Перпендикулярними, якщо вони перетинаються під прямим кутом. Теорема 1. Якщо дві прямі, які перетинаються, паралельні відповідно двом іншим перпендикулярним прямим, то інші прямі теж перпендикулярні. Теорема 2. Через будь-яку точку прямої у просторі можна провести безліч перпендикулярних до неї прямих (див. рисунок). (Усі прямі лежать у […]...
- Теорема про триперпендикуляри Геометрія Стереометрія Теорема про триперпендикуляри Теорема 1. Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна до похилої (див. рисунок). І навпаки: якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої. Приклади застосування теореми про три перпендикуляри 1. На рисунку – куб. , тому […]...
- Перпендикулярність площин Геометрія Стереометрія Перпендикулярність площин Дві площини, що перетинаються, називаються Перпендикулярними, якщо третя площина, перпендикулярна до прямої перетину цих двох площин, перетинає їх по перпендикулярних прямих (див. рисунок). Будь-яка площина, перпендикулярна до прямої перетину перпендикулярних площин, перетинає їх по перпендикулярних прямих. Ознака перпендикулярності площин Теорема 1. Якщо площина проходить через пряму, перпендикулярну до другої площини, то […]...
- Кут між прямою і площиною Урок 54 Тема. Кут між прямою і площиною Мета уроку: формування поняття кута між прямою і площиною, а також умінь учнів знаходити кути між прямою і площиною. Обладнання: стереометричний набір, модель куба. Хід уроку 1. Фронтальне опитування. 1) Дайте означення кута між мимобіжними прямими. 2) Чи залежить кут між мимобіжними прямими від вибору прямих, які […]...
- Кут між площинами Урок 55 Тема. Кут між площинами Мета уроку: формування поняття кута між площинами та вмінь учнів знаходити кути між площинами. Обладнання: стереометричний набір, модель куба. Хід уроку 1. Фронтальне опитування. 1) Що таке кут між прямою і площиною? 2) Чому дорівнює кут між прямою і площиною, якщо відомо, що пряма: А) паралельна площині; Б) перпендикулярна […]...
- Вертикальні кути. Кут між двома прямими, що перетинаються Розділ 2. Взаємне розміщення прямих па площині § 6. Вертикальні кути. Кут між двома прямими, що перетинаються 107. 1) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 15°, дорівнює 15°. 2) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 129°, дорівнює 129°. Відповідь: 1) 15°; […]...
- Вертикальні кути. Кут між прямими Урок № 11 Тема. Вертикальні кути. Кут між прямими Мета: домогтися засвоєння учнями означення вертикальних кутів, формулювання і доведення теореми про властивість вертикальних кутів; означення кутів між прямими. Сформувати вміння: – будувати вертикальні кути; – знаходити вертикальні кути на рисунку; – розв’язувати задачі із застосуванням теореми про рівність вертикальних кутів та суму суміжних кутів. Тип […]...
- Ознака паралельності прямої і площини Геометрія Стереометрія Ознака паралельності прямої і площини Теорема 1. Якщо пряма, яка не належить площині, паралельна якій-небудь прямій у цій площині, то вона паралельна і самій площині. Теорема 2. Якщо пряма паралельна площині, то на цій площині знайдеться пряма, яка паралельна даній прямій. Зверніть увагу: паралельність прямої і площини не означає, що ця пряма паралельна […]...
- Перпендикуляр і похила Геометрія Стереометрія Перпендикуляр і похила Перпендикуляром, опущеним із даної точки на дану площину, називається відрізок, що сполучає дану точку з точкою площини й лежить на прямій, перпендикулярній до площини. Кінець цього відрізка, який лежить у площині, називається Основою перпендикуляра. Відстанню від точки до площини називається довжина перпендикуляра, опущеного із цієї точки на площину. На рисунку […]...
- Кут між прямою та площиною Геометрія Стереометрія Кут між прямою та площиною Кутом між прямою та площиною називається кут між цією прямою і її проекцію (ортогональною) на площину. Якщо пряма перпендикулярна до площини, то кут між нею й площиною вважається таким, що дорівнює , а між паралельними прямою та площиною таким, що дорівнює . Кут між прямою та площиною і […]...
- Розв’язування задач на застосування ознаки перпендикулярності площин Урок 39 Тема. Розв’язування задач на застосування ознаки перпендикулярності площин Мета уроку: формування вмінь учнів застосовувати означення та ознаку перпендикулярності площин до розв’язування задач. Обладнання: стереометричний набір. Хід уроку Фронтальна бесіда за контрольними запитаннями № 11-12 та перевірка виконання задач № 59 (2; 4; 6), 60. Розв’язання задачі № 59 (напівусне) Перпендикулярні площини? і? перетинаються […]...
- Взаємне розміщення прямої та площини і площин у просторі. Перпендикуляр до площини. Взаємне розміщення площин у просторі УРОК № 53 Тема. Взаємне розміщення прямої та площини і площин у просторі. Перпендикуляр до площини. Взаємне розміщення площин у просторі Мета уроку: повторити, привести в систему й розширити відомості про площину та взаємне розміщення двох площин у просторі; ознайомити учнів з різними випадками взаємного розміщення прямої і площини; дати уявлення про перпендикуляр до площини. […]...
- ПОХИЛА ПЛОЩИНА – ПРОСТІ МЕХАНІЗМИ Фізика підготовка до ЗНО комплексне видання МЕХАНІКА 3. ЗАКОНИ ЗБЕРЕЖЕННЯ В МЕХАНІЦІ 3.8. ПРОСТІ МЕХАНІЗМИ 3.8.3. ПОХИЛА ПЛОЩИНА Щоб тіло, яке перебуває на похилій площині, було в стані спокою і рівномірного (без тертя) руху, необхідно прикласти силу, паралельну похилій площині і в стільки ж разів меншу від сили тяжіння, у скільки разів висота похилої площини […]...
- Перпендикулярні площини. Ознака перпендикулярності площин Урок 38 Тема. Перпендикулярні площини. Ознака перпендикулярності площин Мета уроку: формування поняття перпендикулярності площин. Вивчення ознаки перпендикулярності площин. Обладнання: стереометричний набір, моделі куба і прямокутного паралелепіпеда. Хід уроку 1. Перевірити виконання задач № 49, 50 за записами, зробленими до початку уроку на дошці. Нехай AB?; А?, d?; АВ = b, ACD, AC = a (рис. […]...
- Перпендикуляр і похила. Взаємозв’язок між довжинами похилих, проведених з однієї точки, і довжинами їх проекцій Урок 31 Тема. Перпендикуляр і похила. Взаємозв’язок між довжинами похилих, проведених з однієї точки, і довжинами їх проекцій Мета уроку: формування понять: перпендикуляр до площини, похила, основа похилої, основа перпендикуляра, проекції похилої на площину, відстань від точки до площини. Виявлення взаємозв’язку між довжинами двох похилих, проведених з однієї точки до площини, і довжинами їх проекцій. […]...
- Кут між площинами Геометрія Стереометрія Кут між площинами Кут між паралельними площинами вважається таким, що дорівнює . Нехай дані площини перетинаються (див. рисунок). Проведемо площину, перпендикулярну до прямої їх перетину. Ця площина перетинає дані площини по двох прямих. Кут між цими прямими називається Кутом між даними площинами. Означений таким чином кут між площинами не залежить від вибору січної […]...
- Метод координат. Рівняння сфери, площини, прямої Завдання 2 1. 1) Рівняння сфери, усі точки якої рівновіддалені від початку координат на 1 од. має вигляд х2 + у2 + z2= 1. 2) Оскільки центр сфери – початок координат і вона перетинає ось Оz у точці (0; 0; 1), то вона має радіус 1, а значить, її рівняння; х2 + у2 + z2 […]...
- Аксіоми стереометрії Геометрія Стереометрія Аксіоми стереометрії I. Яка б не була пряма, існують точки, що належать цій прямій, і точки, що не належать їй. Через будь-які дві точки можна провести пряму, й тільки одну. II. Із трьох точок на прямій одна й тільки одна лежить між двома іншими. III. Кожний відрізок має певну довжину, більшу від нуля. […]...
- Перпендикулярність прямої і площини. Ознака перпендикулярності прямої і площини Урок 27 Тема. Перпендикулярність прямої і площини. Ознака перпендикулярності прямої і площини Мета уроку: формування поняття прямої, перпендикулярної до площини. Вивчення ознаки перпендикулярності прямої і площини. Обладнання: стереометричний набір, модель куба. Хід уроку 1. Відповіді на запитання, які виникли в учнів при виконанні домашнього завдання. 2. Самостійна робота. Варіант 1 1) Промені OВ, ОС, OD […]...
- Ознака паралельності площин Геометрія Стереометрія Ознака паралельності площин Теорема 1. Якщо дві прямі однієї площини, які перетинаються й відповідно паралельні двом прямим другої площини (див. рисунок), то ці площини паралельні. Теорема 2 (обернена). Якщо в одній площині є дві прямі, які перетинаються, і ці прямі паралельні другій площині, то такі площини паралельні. Зверніть увагу: прямі мають обов’язково перетинатися. […]...
- Розміщення двох площин у просторі. Паралельні площини. Ознака паралельності площин Урок 15 Тема. Розміщення двох площин у просторі. Паралельні площини. Ознака паралельності площин Мета уроку: формування знань учнів про взаємне розміщення двох площин у просторі. Вивчення ознаки паралельності двох площин. Обладнання: стереометричний набір, схема “Взаємне розміщення двох площин”. Хід уроку 1. Перевірити наявність виконаних завдань та відповісти на запитання, які виникли в учнів під час […]...
- ПЕРПЕНДИКУЛЯРНІ І ПАРАЛЕЛЬНІ ПРЯМІ РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ & 5. ПЕРПЕНДИКУЛЯРНІ І ПАРАЛЕЛЬНІ ПРЯМІ Пригадайте, як можуть розташовуватися на площині дві прямі. Якщо вони перетинаються, то утворюють чотири кути – дві пари вертикальних кутів. Йдеться про кути, менші від розгорнутого. Менший із цих кутів вважають кутом між даними прямими. Наприклад, на малюнку 56 прямі АВ і […]...
- Перпендикуляр Геометрія Основні властивості найпростіших геометричних фігур Перпендикуляр Дві прямі називаються Перпендикулярними, якщо вони перетинаються під прямим кутом (див. рисунок), тобто, коли вони перетинаються, утворюються чотири прямих кути. Позначення: . Теорема 1. Через кожну точку прямої можна провести перпендикулярну до неї пряму, і до того ж тільки одну. Перпендикуляром до даної прямої називається відрізок прямої, перпендикулярної […]...
- Тематичне оцінювання № 4 Урок 43 Тема. Тематичне оцінювання № 4 Мета уроку: перевірка навчальних досягнень учнів з теми “Перпендикулярність прямих і площин у просторі”. Хід уроку Тематичне оцінювання № 4 можна провести у вигляді тематичної контрольної роботи. 1. Тематична контрольна робота № 4 Варіант А Варіант 1 1. Побудуйте зображення куба ABCDA1B1C1D1 і запишіть грані куба, які перпендикулярні […]...
- Симетрія відносно площини 334. Якщо відрізок належить площині α, то відрізок симетричний сам собі. Якщо відрізок не лежить в площині: А) Відрізок паралельний площині α АА1 + α; АО = ОА 1 ВВ1 + α; BN = NB, A1В1 симетричний АВ відносно α; Б) Відрізок перетинає площину α. Відрізок А1В1 симетричний відрізку АВ відносно α. 335. Δ А1 […]...
- Ознаки паралельності двох прямих § 3. Паралельні прямі. Сума кутів трикутника 13. Ознаки паралельності двох прямих Практичні завдання 300. 1) Кути АОМ і CEO – відповідні; 2) кути АОЕ і СЕК – відповідні; 3) кути АОE і OED – різносторонні; 4) кути АОЕ і CEO – односторонні. 1) відповідні; 2) односторонні; 3) різносторонні. 301. 1) ∠1 i ∠5; ∠2 […]...
- Існування площини, яка проходить через дану пряму і дану точку УРОК 2 Тема. Існування площини, яка проходить через дану пряму і дану точку Мета уроку: вивчення теореми про існування площини, яка проходить через дану пряму і дану точку, що не лежить на прямій. Обладнання: стереометричний набір. Хід уроку І. Перевірка домашнього завдання 1. Фронтальна бесіда за контрольними запитаннями № 1, 2 §1 із підручника з […]...
- Перетин прямої з площиною. Перерізи многогранників УРОК 3 Тема. Перетин прямої з площиною. Перерізи многогранників Мета уроку: ознайомлення учнів із взаємним розташуванням прямої і площини у просторі. Вивчення теореми про належність прямої до площини. Формування поняття перерізу многогранника. Обладнання: моделі многогранників, схема “Взаємне розташування прямої і площини”, стереометричний набір. 1. Фронтальне опитування. 1) Скільки площин визначають дві прямі, які перетинаються? 2) […]...
- Вертикальні кути Розділ 1. Найпростіші геометричні фігури та їх властивості § 5. Вертикальні кути 152. 1) ∠AYX і ∠BYZ – вертикальні; 2) ∠OLK і ∠MLN – не вертикальні. 153. 1) ∠AOD – вертикальний з кутом 1; 2) ∠АОС і ∠DOB – суміжні з кутом 1. 154. ∠BOA і ∠COD – суміжні. ∠BOA = ∠COD = 60°. 155. […]...
- Розв’язування задач на застосування ознаки перпендикулярності прямої і площини Урок 28 Тема. Розв’язування задач на застосування ознаки перпендикулярності прямої і площини Мета уроку: формування вмінь учнів застосовувати означення та ознаку перпендикулярності прямої і площини до розв’язування задач. Обладнання: стереометричний набір, модель куба. Хід уроку І. Перевірка домашнього завдання 1. Перевірка правильності розв’язання задачі № 7 за записами (з пропусками), зробленими на дошці до початку […]...
- ПЕРПЕНДИКУЛЯРНІ ТА ПАРАЛЕЛЬНІ ПРЯМІ Розділ 5 ВИРАЗИ І РІВНЯННЯ § 33. ПЕРПЕНДИКУЛЯРНІ ТА ПАРАЛЕЛЬНІ ПРЯМІ Ви знаете, що пряма – це геометрична фігура. Дві прямі можуть по-різному розмішуватись на площині. У 6 класі ви дізнаєтеся про перпендикулярні та паралельні прямі. 1. Перпендикулярні прямі Подивиться на перехрестя доріг на малюнку 143. Вибачите, що дороги нагадують прямі, які перетинаються, утворюючи чотири […]...
- Тематичне оцінювання № 3 Урок 34 Тема. Тематичне оцінювання № 3 Мета уроку: перевірка навчальних досягнень учнів з тем “Перпендикулярність прямих”, “Перпендикулярність прямої і площини”. Хід уроку Тематичне оцінювання № 3 можна провести у вигляді тематичної контрольної роботи. 1. Тематична контрольна робота № 3 Варіант А 1. Користуючись зображенням куба ABCDA1B1C1D1 (рис. 180), запишіть ребра куба, які перпендикулярні до […]...
- Розміщення прямої і площини в просторі. Ознака паралельності прямої і площини Урок 13 Тема. Розміщення прямої і площини в просторі. Ознака паралельності прямої і площини Мета уроку: формування знань учнів про взаємне розміщення прямої і площини в просторі. Вивчення ознаки паралельності прямої і площини. Обладнання: стереометричний набір, моделі куба і тетраедра, схема “Аксіоми стереометрії”. Хід уроку І. Аналіз виконання тематичного оцінювання № 1. Зібрати зошити наприкінці […]...
- Властивості прямої і площини, перпендикулярних між собою Урок 30 Тема. Властивості прямої і площини, перпендикулярних між собою Мета уроку: формування знань учнів про властивості перпендикулярних прямих і площин. Обладнання: стереометричний набір, схема “Властивості прямо і площини, перпендикулярних між собою” (с. 116). Хід уроку І. Перевірка домашнього завдання 1. Колективне обговорення розв’язування задачі № 10. 2. Математичний диктант. Дано зображення куба: варіант 1 […]...
- Площа ортогональної проекції многокутника Урок 56 Тема. Площа ортогональної проекції многокутника Мета уроку: вивчення теореми про площу ортогональної проекції многокутника, формування вмінь учнів застосовувати вивчену теорему до розв’язування задач. Обладнання: стереометричний набір, модель куба. Хід уроку 1. Два учні відтворюють розв’язування задач № 42, 45 на дошці. 2. Фронтальне опитування. 1) Дайте означення кута між двома площинами, які перетинаються. […]...
- Властивість точки, рівновіддаленої від вершин многокутнику Урок 32 Тема. Властивість точки, рівновіддаленої від вершин многокутнику Мета уроку: формування знань про властивість точки, рівновіддаленої від вершин многокутника, та вмінь застосовувати цю властивість до розв’язування задач. Обладнання: стереометричний набір, схема “Коло, описане навколо многокутника”. Хід уроку 1. Перевірити розв’язання задачі № 24 за записами (з пропусками), зробленими на дошці до початку уроку. Розв’язання […]...