Множення різниці двох виразів на їх суму
Розділ 1. ЦІЛІ ВИРАЗИ
& 15. Множення різниці двох виразів на їх суму
Помножимо різницю а – b на суму а + b:
(а – b)(а + b) = а2 + ab – bа – b2 = а2 – b2.
Отже,
Одержали ще одну формулу скороченого множення. Її читають так.
Розглянемо приклади застосування цієї формули.
Приклад 1. Виконати множення:
1) (2m – 3р)(2m + 3р);
2) (4а2 + b3)(b3 – 4а2).
Р о з в’ я з а н н я.
1) (2m – 3p)(2m + 3р) = (2m)2 – (3р)2 = 4m2 – 9р2, або скорочено: (2m – 3р)(2m + 3р) = 4m2 – 9р2.
2) (4а2 + b3)(b3 – 4а2) = (b3 + 4а2)(b3 – 4а2) = (b3)2 – (4а2)2 = b6 – 16а4.
Приклад
Р о з в’ я з а н н я.
1-й спосіб.
Винесемо у виразі – 5m – 7а за дужки -1. Матимемо:
(-5m – 7а)(5m – 7а) = -1 ∙ (5m + 7а)(5m – 7а) = -((5m)2 – (7а)2) = (25m2 – 49а2) = -25m2 + 49а2 = 49а2 – 25m2.
2-й спосіб.
У кожному із множників спочатку поміняємо місцями доданки:
(-5m – 7а)(5m – 7а) = (-7а – 5m)(-7а + 5m) = (-7а)2 – (5m)2 = 49а2 – 25m2.
Приклад 3. Обчислити зручним способом 4,3 ∙ 3,7.
Р о з в ‘я з а н н я.
4,3 ∙ 3,7 = (4 + 0,3)(4 – 0,3) = 42 – 0,32 = 16 – 0,09 = 15,91.
Якому виразу дорівнює добуток різниці двох виразів на їх суму? Запишіть і прочитайте відповідну формулу.
490.
1) (а – m)(а + m) = а2 – m2;
2) (с + р)(с – р) = с2 + р2;
3) (b – х)(b + x) = (b – x)2;
4) (d + n)(d – n) = n2- d2?
491. Закінчіть запис:
1) (а – 5)(а + 5) = а2 – 52 = … ;
2) (m + 7)(m – 7) = m2 – 72 = … .
492. Знайдіть добуток:
1) (х – у)(х + у);
2) (р + q)(р – q).
493. Виконайте множення двочленів:
1) (m + n)(m – n);
2) (с – d)(c + d).
494. Виконайте множення:
1) (р – 9)(р + 9);
2) (5 + х)(5 – х);
3) (3 – с)(3 + с);
4) (7 + у)(у – 7).
495. Перетворіть на многочлен:
1) (m – 2)(m + 2);
2) (7 + а)(7 – а);
3) (4 – х)(4 + х);
4) (11 + b)(b – 11).
496. Подайте добуток у вигляді многочлена:
1) (2х – 3)(2х + 3);
2) (3р + 8)(3р – 8);
3) (4 + 5а)(5а – 4);
4) (3mn – 4р)(4р + 3m);
5) (7а 4- 10b)(10b – 7а);
6) ( P –
P –  Q) (
Q) ( Q +
Q +  Р).
Р).
497. Виконайте множення:
1) (р – 2m)(р + 2m);
2) (2р + 7)(2р – 7);
3) (2с + 5)(5 – 2с);
4) (8а – 0,3х)(0,3x + 8а);
5) (0,1р + q) (q – 0,1р);
6) ( А –
А –  B)(
B)(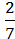 A +
A +  B).
B).
498. Заповніть у зошиті таблицю за зразком:
Вираз І | Вираз II | Добуток різниці виразів І і ІІ на їх суму | Різниця квадратів виразів І і II |
3а | B | (2а – b)(3а + b) | 9a2 – b2 |
5m | 2n | ||
| 3y | ||
0,1р | 0,7q | ||
|
|
499. Виконайте дії:
1) 16 + (3а + 4)(3а – 4);
2) (5m – 3)(5m + 3) – 25m2.
500. Спростіть вираз:
1) (8x – 5)(8x + 5) + 25;
2) 9m2 + (5 – 3m)(5 + 3m);
3) (2b – 3)(3 + 2b) – 4b2;
4) (4а + 7)(7 – 4а) – 49.
501. Розв’яжіть рівняння:
1) 3х = (2х – 3)(2х + 3) – 4х2;
2) 9х2 + (8 – 3х)(8 + 3х) = 4х.
502. Знайдіть корені рівняння:
1) 8х = (5х – 4)(5х + 4) – 25х2;
2) (9 – 4x)(x9 + 4х) + 16х2 = 3х.
503. Обчисліть зручним способом:
1) (40 – 1)(40 + 1);
2) 81 ∙ 79;
3) 1002 ∙ 998;
4) 1,03 ∙ 0,97.
504. Знайдіть значення виразу зручним способом:
1) (80 + 2)(80 – 2);
2) 39 ∙ 41;
3) 108 ∙ 92;
4) 12,3 ∙ 11,7.
505. Подайте добуток у вигляді многочлена:
1) (р2 + 3q)(3q – р2);
2) (2а – m3)(m3 + 2а);
3) (5а – b2)(b2 + 5а);
4) (0,7m + n2)(0,7m – n2);
5) (4t2 – р4)(4t2 + р4);
6) (3а3 – 4b4)(4b4 + 3а3).
506. Виконайте множення:
1) (1,7а – 1,4р3)(1,4p3 + 1,7а);
2) (3a7 –  B3)(
B3)(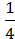 b3 + 3a2);
b3 + 3a2);
3) (5m2n +  P3)(
P3)(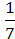 p3 – 5m2n);
p3 – 5m2n);
4) ( a7 + 1,2y8)(1,2y8 –
a7 + 1,2y8)(1,2y8 –  A7);
A7);
507. Виконайте множення:
1) (5а + b)(b2 – 5а);
2) (4а3 – d2)(d2 + 4а3);
3) (0,7р – m7)(m7 + 0,7р);
4) ( m2 + 3b7)(3b7 –
m2 + 3b7)(3b7 –  P7);
P7);
5) (0,2а2b – 0,3аb2)(0,2а2b + 0,3аb2);
6) (1,2 p7 –  A8)(
A8)(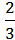 a8 + 1,23p7).
a8 + 1,23p7).
508. Подайте у вигляді многочлена:
1) (-а2 + 7)(7 + а2);
2) (-р2 – q7)(p2 – q7);
3) ( 8m – 5р)( 8m + 5р);
4) ( 2а3 – 3b)( 3b + 2а3).
509. Перетворіть на многочлен:
1) (-а7 + b5)(а7 + b5);
2) (-0,1m3 – p4)(0,1m3 – р4);
3) (3х – 2р)(3х + 2р)(9х2 + 4р2);
4) (-а2 – 5b3)(а2 – 5b3)(a4 + 25b8).
510. Спростіть вираз:
1) (а – b)(а + b)(а2 + b2);
2) (2а + х)(4а2 + х2)(2а – х);
3) (с3 + d2)(c3 – d2)(d4 + с8);
4) (-x – у)(х – у)(х2 + y2)(х4 + у4).
511. Замість зірочки запишіть такі одночлени, щоб утворилася тотожність:
1) (2а 4 *)(2а – *) = 4а2 – 49b2;
2) (* – 9р)(* + 9р) = 0,25m4 – 81р2;
3) 100а8 – 9b8 = (* + 10а)(10а4 – *);
4) (4х – 3у)(* + *) = 16х2 – 9y2.
512. Знайдіть корені рівняння:
1) 8х(1 + 2х) – (4х + 1)(4х – 1) = 17;
2) х – 12х(1 – 3х) = 14 – (5 – 6х)(6х + 5);
3) (4х + 1)(4х – 1) + (2х – 3)2 = 5х(4х – 11).
513. Розв’яжіть рівняння:
1) 5х(4х – 1) – (6х – 1)(6х + 1) = (4х + 3)(3 – 4х);
2) (3х – 4)(3х + 4) – (5х – 2)(5х + 2) – 2х(1 – 8х);
3) (5х – 4)2 – 2х(8х – 5) = (3х – 2)(3х + 2).
514. Спростіть:
1) (а + 3)2 – (а + 3)(а – 3);
2) (8х – 3у)(8х + 3у) (3х – 8у)2;
3) ( b – 3)2(b + 3)2;
4) (а + 5)2(5 – а)2.
515. Спростіть вираз:
1) (с – 2)2 – (с – 3)(с + 3);
2) (9х – 2у)(9х + 2у) – (5х – 2у)2;
3) (а + 6)2(а – 6)2;
4) (2 – m)2(m + 2)2.
516. Доведіть, що квадрат будь-якого цілого числа завжди перевищує добуток попереднього і наступного чисел на одиницю.
517. Викопайте множення, використавши формули скороченого множення:
1) ((х + у) + 1)(((х + у) – 1);
2) (а + b + с)(а – (b + с));
3) (m + n + 2р)(m + n – 2р);
4) (х – у – 2)(х + у + 2).
Вправи для повторення
518. Обчисліть: 2,7 ∙ (8 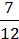 – 2
– 2 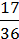 ) – 4
) – 4  : 0,65.
: 0,65.
519. Щоб заасфальтувати деяку ділянку дороги за певний час, бригада шляховиків мала асфальтувати по 15 м2 щогодини. Натомість щогодини вони асфальтували на 3 м2 більше, тому за 2 год до закінчення терміну їм залишилося заасфальтувати 12 м2. Якою була площа ділянки та скільки годин її мали асфальтувати?
Цікаві задані для учнів неледачих
520. Нехай а1; а2; а3 – натуральні числа, b1; b2; b3 – ці самі числа, записані в іншому порядку. Доведіть, що добуток |а1 – b1,| ∙ |а2 – b2| ∙ |а3 – b3| є парним числом.
