Головна ⇒ 📌Довідник з геометрії ⇒ Об’єм кулі
Об’єм кулі
Геометрія
Об’єми тіл
Об’єм кулі
На рисунку зображено кулю, кульовий сегмент і кульовий сектор.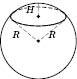
Об’єм кулі:
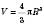 , де R – радіус кулі.
, де R – радіус кулі.
Об’єм кульового сегмента:
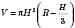 , де H – висота кульового сегмента,
, де H – висота кульового сегмента,
R – радіус кулі.
Об’єм кульового сектора:
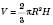 , де R – радіус кулі, H – висота відповідного кульового сегмента.
, де R – радіус кулі, H – висота відповідного кульового сегмента.
Іноді треба знайти об’єм або площину поверхні тіла обертання. Щоб правильно
1. Відрізок обертається навколо осі, на якій лежить один із його кінців (див. рисунок нижче зліва).
l – пряма. Проведемо
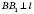 . Отже, точка
. Отже, точка 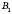 є проекцією B на пряму l. Відрізок AB, обертаючись навколо осі, утворює бічну поверхню конуса з вершиною A, висотою
є проекцією B на пряму l. Відрізок AB, обертаючись навколо осі, утворює бічну поверхню конуса з вершиною A, висотою 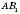 і радіусом основи
і радіусом основи 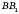 .
.2. Відрізок обертається навколо осі, якій він є паралельним (див. рисунок нижче
Спроектуємо точки A і B на вісь l.
Дістанемо точки
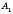 і
і 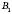 .
.Очевидно, що при обертанні AB навколо l дістанемо бічну поверхню прямого кругового циліндра, у якого AB – твірна, вісь – пряма l, радіус основи –
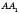 .
.
3. Відрізок обертається навколо осі (див. рисунок), він не є їй паралельним і лежить з нею в одній площині, не перетинаючи осі.
Нехай точки
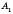 і
і 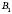 – проекції точок A і B на вісь l відповідно.
– проекції точок A і B на вісь l відповідно.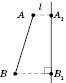
При обертанні AB навколо l дістанемо бічну поверхню зрізаного конуса, у якого AB – твірна,
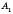 – центр верхньої основи,
– центр верхньої основи, 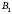 – центр нижньої основи,
– центр нижньої основи, 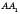 – радіус верхньої основи,
– радіус верхньої основи, 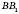 – радіус нижньої основи.
– радіус нижньої основи.Якщо навколо осі обертається який-небудь многокутник, треба спроектувати на вісь обертання всі вершини многокутника й розібрати, які фігури утворюють усі його сторони при обертанні.




 (1 votes, average: 5.00 out of 5)
(1 votes, average: 5.00 out of 5)Related posts:
- Циліндр, описаний навколо кулі Геометрія Комбінації геометричних тіл Циліндр, описаний навколо кулі Площина, проведена через центр кулі паралельно твірним циліндра (рисунок нижче зліва), є площиною симетрії тіла. У цьому випадку висота циліндра дорівнює діаметру кулі. В осьовому перерізі цього тіла отримаємо прямокутник, у який вписане коло (рисунок справа). Але із цього випливає, що осьовий переріз даного циліндра – квадрат. […]...
- Описані кулі Геометрія Комбінації геометричних тіл Описані кулі Кожна грань вписаного у сферу многогранника є вписаним у деяке коло многокутником. Основи перпендикулярів, які опущені з центра описаної кулі на площини граней, є центрами описаних навколо граней кіл. Отже, центром кулі, описаної навколо многогранника, є точка перетину перпендикулярів до площини граней, які проведені через центри кіл, описаних навколо […]...
- Конус, вписаний у кулю Геометрія Комбінації геометричних тіл Конус, вписаний у кулю Вершина конуса лежить на сфері (рисунок нижче зліва). Основа конуса лежить на сфері. Комбінація є симетричною відносно площини, що містить вісь конуса. У такому перерізі дістанемо трикутник, вписаний у коло (рисунок справа). Трикутник рівнобедрений. Бічні сторони – твірні конуса, коло – велике коло описаної кулі. Отже, радіус […]...
- Властивості сфери і кулі 1. Відстань, яка б відділяла мене від мого антипода дорівнювала б Двом радіусам Землі. Відповідь: 2R Землі. 2. Нехай АО – радіус Землі, ОА = 6400 км, О1А – радіус Полярного кола Землі. Координати Полярного кола Землі 66°31′ п. ш. ∠АОВ = 66°31′; ∠О1ОА = 90° – 67° = 23°. З ΔO1ОA: Ο1Α = ОА […]...
- Циліндр Геометрія Тіла обертання Циліндр Круговим циліндром називається тіло, яке складається з двох кругів, що не лежать в одній площині й суміщаються паралельними перенесенням, і всіх відрізків, що сполучають відповідні точки цих кругів (див. рисунок). Круги називаються Основами циліндра, а відрізки, що сполучають точки кіл кругів, – Твірними циліндра. Основи циліндра рівні й лежать у паралельних […]...
- Куля. Площа поверхні та об’єм кулі УРОК № 58 Тема. Куля. Площа поверхні та об’єм кулі Мета уроку: повторення, приведення в систему й розширення відомостей про кулю (сферу), площу поверхні та об’єм кулі; формування вмінь учнів знаходити площі поверхонь і об’єми куль. Тип уроку: комбінований. Наочність і обладнання: таблиця “Початкові відомості стереометрії” [13]; моделі куль. Вимоги до рівня підготовки учнів: пояснюють, […]...
- Об’єми кулі та її частини. Площа сфери 1. Обчислимо площу поверхні Землі: S= 4πR2 = 4π · 63752. Площа суші складає Відповідь: π × 63752. 2. Знайдемо об’єм кавуна радіуса 10 см: На одного їдока приходиться Знайдемо об’єм кавуна-радіусом 20 см: На одного їдока приходиться Відповідь: у вісьмох. 3. Оскільки передбачається, що каша у двох котлах однакова, То в другому казані відношення […]...
- Об’єм кулі та її частин 1338. А) Нехай ABCDA1В1C1D1 – куб. Оскільки куля вписана в куб з ребром а, то 2г = а, Отже, об’єм кулі Б) Оскільки діагональ куба дорівнює двом радіусам кулі, то знайдемо діагональ З ΔB1BD: Отже, радіус, кулі Об’єм кулі V дорівнює: Відповідь: а) б) 1339. Нехай SA – твірна конуса. ∠SAO = α. З ΔSAO: […]...
- Циліндр, вписаний у кулю Геометрія Комбінації геометричних тіл Циліндр, вписаний у кулю Основи циліндра є рівновіддаленими від центра кулі (рисунок нижче зліва). Ця комбінація тіл є симетричною відносно будь-якої площини, що проходить через центр кулі паралельно твірним циліндра. У перерізі тіла такою площиною дістанемо прямокутник і описане навколо нього коло (рисунок справа). Прямокутник ABCD є осьовим перерізом циліндра, а […]...
- Куля, вписана в конус Геометрія Комбінації геометричних тіл Куля, вписана в конус Площина, яка містить вісь конуса, є площиною симетрії (рисунок нижче зліва). Осьовий переріз комбінації є рівнобедреним трикутником, у який вписане коло (рисунок справа). Трикутник – це осьовий переріз конуса, тобто – твірні конуса, AB – діаметр основи конуса, а коло – велике коло вписаної кулі. Отже, радіус […]...
- ЦИЛІНДР. КОНУС. КУЛЯ Розділ 3 ВІДНОШEННЯ І ПРОПОРЦІЇ § 18. ЦИЛІНДР. КОНУС. КУЛЯ У 5 класі ви вже ознайомилися з просторовими фігурами: прямокутним паралелепіпедом і кубом. ь на малюнок 56. Ви бачите предмети, які використовують у побуті. У сі вони мають одну й ту саму форму – циліндра (мал. 57). Мал. 56 Мал. 57 Мал. 58 Maл. 59 […]...
- Вписані кулі Геометрія Комбінації геометричних тіл Вписані кулі Якщо куля вписана в призму, то в її перпендикулярний переріз можна вписати коло. Висота призми дорівнює діаметру кола, вписаного в перпендикулярний переріз призми, тобто діаметру вписаної кулі. Центр кулі – середина висоти призми, що проходить через центр кола, яке вписане в перпендикулярний переріз. Центр кулі, яка вписана в пряму […]...
- Куля Геометрія Тіла обертання Куля Кулею називається тіло, що складається з усіх точок простору, які розташовані від даної точки на відстані, що не більша за дану. Ця точка називається Центром кулі, а дана відстань – Радіусом кулі. Межа кулі називається Кулевою поверхнею, або Сферою. Відрізок, що сполучає дві точки кульової поверхні й проходить через центр кулі, […]...
- Тіла і поверхні обертання 905. На рисунку тіло, утворене обертанням прямокутника навколо його сторони. 906. А) Тіло, утворене обертанням прямокутного трикутника навколо катета, Б) Тіло, утворене обертанням прямокутного трикутника навколо гіпотенузи. ΔABC – прямокутний, AB – гіпотенуза. 907. Площина симетрії тіла обертання проходить через його вісь. 908. Див. рис. 909. У площині прямокутника ззовні його і паралельно одній з […]...
- Конус. Площа поверхні та об’єм конуса УРОК № 57 Тема. Конус. Площа поверхні та об’єм конуса Мета уроку: повторення, приведення в систему й розширення відомостей про конус, площу поверхні та об’єм конуса; формування вмінь учнів знаходити площі поверхонь і об’єми конусів. Тип уроку: комбінований. Наочність і обладнання: таблиця “Початкові відомості стереометрії” [13]; моделі конусів. Вимоги до рівня підготовки учнів: пояснюють, що […]...
- Перпендикуляр і похила Геометрія Стереометрія Перпендикуляр і похила Перпендикуляром, опущеним із даної точки на дану площину, називається відрізок, що сполучає дану точку з точкою площини й лежить на прямій, перпендикулярній до площини. Кінець цього відрізка, який лежить у площині, називається Основою перпендикуляра. Відстанню від точки до площини називається довжина перпендикуляра, опущеного із цієї точки на площину. На рисунку […]...
- ЧОМУ БУВАЄ ДЕНЬ І НІЧ? ГОТУЄМОСЬ ДО МАДРІВОК ПОРАМИ РОКУ ПРИРОДА I ПОГОДА Зустріч 4. ЧОМУ БУВАЄ ДЕНЬ І НІЧ? Ти дізнаєшся, що Земля обертається навколо своєї вісі; чому буває день і ніч; що таке доба. Пригадай! Як називається модель земної кулі? – Як добре, – сказав їжачок Хитрячок, – що люди придумали глобус. Завдяки глобусу можна дізнатися не тільки […]...
- Пропорційність відрізків хорд і січних кола Геометрія Кути, пов’язані з колом Пропорційність відрізків хорд і січних кола Теорема 1. Якщо хорди AB і CD кола перетинаються в точці S, то (рисунок 1). Теорема 2. Якщо з точки P до кола проведені дві січні, що перетинають коло відповідно в точках A, B, C, D, то (рисунок 2). Тобто добуток січної, проведеної до […]...
- Описана піраміда Геометрія Комбінації геометричних тіл Описана піраміда Якщо вершина піраміди проектується в центр кола, яке є вписаним в основу піраміди, то центр вписаної кулі – точка перетину висоти піраміди з бісектрисою лінійного кута двогранного кута при ребрі основи. У будь-яку правильну піраміду можна вписати кулю, центр якої лежить на висоті піраміди. Точки дотику кулі й бічних […]...
- Конуси 1050. ΔSAPO: ∠АОР = 90°, ОЕ = АЕ = ЕР = 6,5 см → АР = 13 см. АО = 5 см. R = AO, L = АР = 13 см, r = 5 см. Sп. к. = πrl + πr2 = π(5 × 13 + 52) = 90π. S = 90π см2. 1051. ΟΑ […]...
- Коло Геометрія Основні властивості найпростіших геометричних фігур Коло Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки. Ця точка називається Центром кола. Відстань від точок кола до його центра називається Радіусом кола. Радіусом також називається будь-який відрізок, що сполучає точку кола з його центром. Відрізок, що сполучає дві точки кола, називається Хордою. […]...
- Інші комбінації геометричних тіл Геометрія Комбінації геометричних тіл Інші комбінації геометричних тіл Конус є вписаним у циліндр (див. рисунок нижче), коли основа конуса збігається з нижньою основою циліндра, а вершина конуса – центр верхньої основи циліндра. Осі циліндра і конуса в цьому випадку збігаються. Циліндр, вписаний у конус (див. рисунок нижче), якщо нижня основа циліндра лежить на основі конуса, […]...
- Симетрія відносно точки Геометрія Рух Симетрія відносно точки Нехай O – фіксована точка, X – довільна точка площини. Відкладемо на продовженні відрізка OX за точку O відрізок , що дорівнює OX. Точка називається Симетричною точці X відносно точки O (див. рисунок). Очевидно, що точка, симетрична , є точка X. Перетворення фігури F у фігуру , при якому кожна […]...
- Поворот Геометрія Рух Поворот Поворотом площини навколо даної точки називається такий рух, при якому кожний промінь, що виходить із даної точки, повертається на один і той самий кут в одному й тому самому напрямку (див. рисунок)....
- Конус Геометрія Тіла обертання Конус Круговим конусом називається тіло, яке складається з круга – Основи конуса, точки, яка не лежить у площині цього круга, – Вершини конуса і всіх відрізків, що сполучають вершину конуса з точками основи. Відрізки, що сполучають вершину конуса з точками кола основи, називаються Твірними конуса. Конус називається Прямим (далі просто “конус”), якщо […]...
- Рівняння кола УРОК № 26 Тема. Рівняння кола Мета уроку: виведення рівняння кола. Формування вмінь учнів використовувати рівняння кола до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють рівняння кола. Розпізнають рівняння кола. Хід уроку I. Перевірка домашнього завдання Перевірити наявність […]...
- Сфера – СТЕРЕОМЕТРІЯ Формули й таблиці МАТЕМАТИКА СТЕРЕОМЕТРІЯ Сфера Кільцевий сегмент – частина кулі, що відсікається від неї площиною. S = 2πR·H, Де R – радіус кулі, Н – висота сегмента. Круговий сегмент – частина кулі, отримана таким чином: якщо кільцевий сегмент менший від півкулі, тоді його доповнюють конусом, вершина якого є центром кулі, а основою є основа […]...
- НАША ПЛАНЕТА ВСТУП НАША ПЛАНЕТА – ЗЕМЛЯ. ЧОМУ НА ЗЕМЛІ БУВАЮТЬ ДЕНЬ І НІЧ Яку форму має наша Земля, плоску чи кулясту? Нині це запитання нікого не здивує, бо всі знають, що Земля має форму кулі. Її так і називають “земна куля”. Побачив нашу планету з великої висоти 12 квітня 1961 року перший космонавт Землі – Юрій […]...
- ЧОМУ НА ЗЕМЛІ ІСНУЮТЬ ПОРИ РОКУ ВСТУП ЧОМУ НА ЗЕМЛІ ІСНУЮТЬ ПОРИ РОКУ Пригадай, що тобі відомо про рух Землі навколо своєї осі. Які бувають пори року? Здавна люди помітили, що коли Сонце піднімається високо на небосхилі, – на Землі тепло, а коли опускається низько, – холодно. Теплі пори року (весна, літо) змінюються холодними (осінь, зима), тому що Земля обертається не […]...
- КУЛІ Чарлз Хортон Соціологія короткий енциклопедичний словник КУЛІ Чарлз Хортон (1864 – 1929) – амер. соціолог, проф. Мічиганського ун-ту, один з основоположників інтеракціоністського напряму в соціології, автор концепцій малих груп та “дзеркального “Я”. Намагаючись подолати протиставлення особи й суспільства, індивідуального та соціального, К. у своїх працях “Природа людини і соціальний порядок” (1902), “Соціальна організація” (1909), “Соціальний процес” (1918) […]...
- Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Візьмемо три взаємно перпендикулярні прямі Oх, Oy, Oz, які перетинаються в одній точці О (див. рисунок). Проведемо через кожну пару цих прямих площину. Площина, яка проходить через прямі Oх і Oу, називається площиною Oxy. Дві інші площини називаються відповідно Oxz і Oyz. Прямі Ox, Oy, Oz називаються Координатними […]...
- Властивості конуса 1. 1) Твірна конуса не може утворювати з його основою прямий кут, оскільки Вона є гіпотенузою трикутника обертання, яка утворює бічну поверхню конуса. 2) Теж не може (обгрунтування у п. 1). Якщо конус зрізаний 1) ні; 2) так. Відповідь: 1) ні; 2) ні для зрізаного конуса 1) ні, 2) так. 2. Нехай SA – твірна […]...
- Циліндр 940. Нехай дано циліндр, ABCD – осьовий переріз циліндра, AO = r – радіус циліндра, AC = d – діагональ осьового перерізу: А) ΔABC — прямокутний. BC – висота циліндра; Б) SABCD – площа діагонального перерізу. В) Площа бічної поверхні: Г) Площа поверхні циліндра 941. Нехай дано циліндр, діагональ осьового перерізу циліндра дорівнює D і […]...
- Види опадів і закономірності їхнього розподілу на земній кулі РОЗДІЛ 3 ГЕОГРАФІЧНА ОБОЛОНКА Тема 2. Атмосфера § 39. Види опадів і закономірності їхнього розподілу на земній кулі Пригадайте Які опади найчастіше бувають у вашій місцевості? Коли випадає сніг? Народжені хмарами. Вода, яка випадає з хмар у вигляді дощу, снігу, крупи, граду, є атмосферними опадами. Опади дають лише ті хмари, у яких краплини води і […]...
- Точки та лінії небесної сфери § 2. Основи практичної астрономії 2. Точки та лінії небесної сфери На небесній і земній сферах можна провести деякі кола, за допомогою яких визначаються небесні координати світил (рис. 2.3, а). На земній сфері існують дві особливі точки – географічні полюси, де вісь обертання Землі перетинає поверхню планети (N, S – відповідно Північний та Південний полюси). […]...
- Висота, бісектриса, медіана трикутника Геометрія Основні властивості найпростіших геометричних фігур Висота, бісектриса, медіана трикутника Висотою Трикутника, опущеною з даної вершини, називається перпендикуляр, проведений із цієї вершини до прямої, що містить протилежну сторону трикутника. У кожному трикутнику можна провести три висоти. Висоти трикутника (або прямі, що їх містять) перетинаються в одній точці. На рисунках зображено, як перетинаються висоти в гострокутному […]...
- Циліндр. Площа поверхні та об’єм циліндра УРОК № 56 Тема. Циліндр. Площа поверхні та об’єм циліндра Мета уроку: повторення, приведення в систему й розширення відомостей про циліндр, площу поверхні та об’єм циліндра; формування вмінь учнів знаходити площі поверхонь і об’єми циліндрів. Тип уроку: комбінований. Наочність і обладнання: таблиця “Початкові відомості стереометрії” [13]; моделі циліндрів. Вимоги до рівня підготовки учнів: пояснюють, що […]...
- Розв’язування найпростіших тригонометричних нерівностей Математика – Алгебра Тригонометричні функції Розв’язування найпростіших тригонометричних нерівностей Найзручнішим є спосіб розв’язування тригонометричних нерівностей за допомогою тригонометричного кола. Приклади 1) . Побудуємо одиничне коло (див. рисунок нижче). Проведемо пряму . Вона перетинає коло у двох точках. Одна з них відповідає куту або , друга – куту або . Ці дві точки розбивають коло на […]...
- Промінь, пряма, площина Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 17. Промінь, пряма, площина Продовжимо відрізок АВ за допомогою лінійки за точку В (рис. 38). На рисунку таке продовження обмежене розмірами аркуша, але можна уявити, що ми продовжили відрізок необмежено. Якщо продовжити відрізок АВ за його кінець В необмежено, то одержимо промінь […]...
- Земля як планета Географія Загальна географія Земля в космічному просторі Земля як планета Форма та розміри Землі Земля – третя від Сонця планета Сонячної системи. За сучасними уявленнями, Земля утворилася близько 4,7 млрд років тому. Наша планета має кулясту форму (геоїд) і обертається навколо Сонця зі швидкістю 29,765 км/с, або 108 000 км/год. Вісь Землі має нахил 66°33′22″, […]...