Обернені тригонометричні функції: у = arcsin х, у = arccos х
УРОК 18
Тема. Обернені тригонометричні функції: у = arcsin х, у = arccos х
Мета уроку: вивчення властивостей обернених тригонометричних функцій: у = arcsin х, у = arccos х.
І. Перевірка домашнього завдання
Математичний диктант.
Закінчіть математичні твердження:
1. Функція, яка набуває кожного свого значення в єдиній точці області визначення називається…
2. Оберненою до функцій у = х + 3 є функція…
3. Оберненою до функцій у = 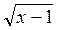 є функція…
є функція…
4. Оберненою до функцій у = х2, х > 0 є функція…
5. Графіки даної
6. Якщо дана функція у = f(x) – зростаюча, то обернена до неї функція…
7. Область визначення функції у = f(x), для оберненої функції буде областю…
8. Область значень функції у == f(x) для оберненої функції буде областю…
Відповідь: 1. оборотною. 2. у = х – 3. 3. у = х2 + 1, х [0; +
[0; + ). 4. у =
). 4. у =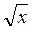 . 5. відносно прямої у = х. 6. зростаюча. 7. значень. 8. визначення.
. 5. відносно прямої у = х. 6. зростаюча. 7. значень. 8. визначення.
II. Сприймання і усвідомлення поняття arcsin? і властивостей функції у = arcsin х
Як ви знаєте, функція у = sin х зростає на проміжку 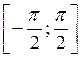 і приймає
і приймає
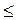 1 на проміжку
1 на проміжку 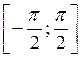 має єдиний корінь, який називається арксинусом числа а і позначається arcsin a.
має єдиний корінь, який називається арксинусом числа а і позначається arcsin a.Арксинусом числа а називається таке число із проміжку 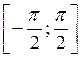 Синус якого дорівнює а.
Синус якого дорівнює а.
Приклад 1. Знайдемо arcsin  .
.
Arcsin  =
=  , бо sin
, бо sin  =
=  і
і 

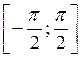 .
.
Приклад 2. Знайдемо arcsin 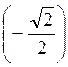
Arcsin 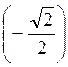 =
= 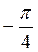 , бо sin
, бо sin 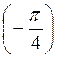 =
= 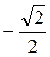 і
і 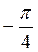

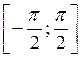 .
.
Виконання вправ________________________
1. Обчисліть:
A) arcsin 0; б) arcsin 1; в) arcsin (-1); г) arcsin 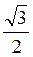 ; д) arcsin
; д) arcsin 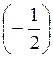 ; є) arcsin
; є) arcsin 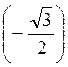
Відповідь: a) 0; б)  ; в) –
; в) – ; г)
; г)  ; д) –
; д) – ; e) –
; e) –  .
.
2. Які із поданих виразів мають смисл і чому:
A) arcsin 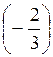 ; б) arcsin 1,5; в) arcsin?; г) arcsin
; б) arcsin 1,5; в) arcsin?; г) arcsin 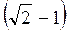 ; д) arcsin
; д) arcsin 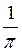 ?
?
Відповідь: а); г); д).
3. Знайдіть:
А) arcsin 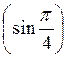 ; б) sin
; б) sin 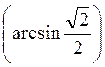 .
.
Відповідь: а)  ; б)
; б) 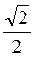 .
.
Оскільки кожному значенню х  [-1; 1] можна поставити у відповідність єдине значення arcsin x, то можна говорити, що існує функція у = arcsin х.
[-1; 1] можна поставити у відповідність єдине значення arcsin x, то можна говорити, що існує функція у = arcsin х.
Графік функції у = arcsin х одержимо із графіка функції у = sin х, х 
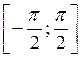 перетворенням симетрії відносно прямої у = х (рис. 110). Розглянемо властивості функції у = arcsin х.
перетворенням симетрії відносно прямої у = х (рис. 110). Розглянемо властивості функції у = arcsin х.
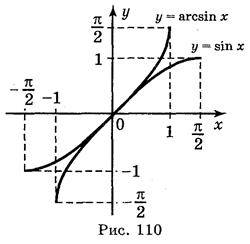
1. D(y) = [-1; 1].
2. Е(у) = 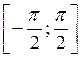 .
.
3. Графік симетричний відносно початку координат (функція непарна) arcsin (-х) = – arcsin х.
4. Функція зростаюча. Якщо х1 > х2 то arcsin х1 > arcsin х2
5. у = 0, якщо х = 0.
6. уmах = y(1) =  , ymіn = y(-1) = –
, ymіn = y(-1) = – .
.
Виконання вправ
1. Порівняйте числа:
A) arcsin 0,3 і arcsin 0,2;
Б) arcsin 0,3 і arcsin (-0,3);
В) arcsin 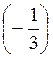 і arcsin
і arcsin 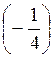 .
.
Відповідь: a) arcsin 0,3 > arcsin 0,2;
Б) arcsin 0,3 > arcsin (-0,3);
В) arcsin 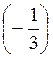 < arcsin
< arcsin 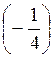 .
.
2. Розташуйте в порядку зростання:
A) arcsin 0,4; arcsin 0,2; arcsin 0,8;
Б) arcsin (-0,1); arcsin (-0,2); arcsin (-0,3);
В) arcsin ; arcsin (-0,3); arcsin 0,9.
; arcsin (-0,3); arcsin 0,9.
Відповідь: a) arcsin 0,2; arcsin 0,4; arcsin 0,8;
Б) arcsin (-0,3); arcsin (-0,2); arcsin (-0,1);
В) arcsin (-0,3); arcsin  ; arcsin 0,9.
; arcsin 0,9.
3. Знайдіть область визначення функцій:
А) у = arcsin (х + 1);
Б) у = arcsin (х2 – 1);
В) у = arcsin 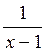 ;
;
Г) у = arcsin 5х.
Відповідь: а) х [-2; 0]; б) х
[-2; 0]; б) х [-
[-  ;
;  ]; в) х
]; в) х (-
(- ; 0] U [2; +
; 0] U [2; + ); г) х
); г) х [-0,2; 0,2].
[-0,2; 0,2].
4. Знайдіть область значень функцій:
А) у = arcsin 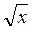 ; б) у = arcsin
; б) у = arcsin 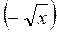 .
.
Відповідь: а) у
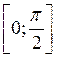 ; б) у
; б) у
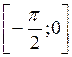 .
.
5. Побудуйте графіки функцій:
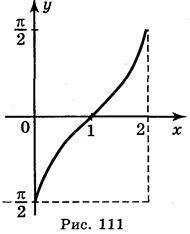
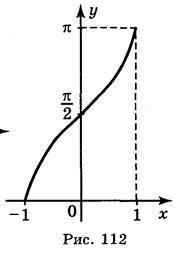
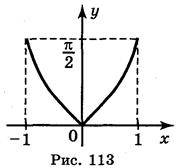
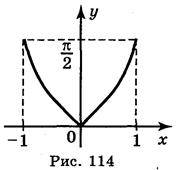
А) у = arcsin (х – 1); б) y =  + arcsin х ; в) у = arcsin | х |; г) у = | arcsin х |.
+ arcsin х ; в) у = arcsin | х |; г) у = | arcsin х |.
Відповідь: а) рис. 111; б) рис. 112; в) рис. 113; г)рис. 114.
III. Сприймання і усвідомлення поняття arccos a і властивостей функції у = arccos x
Функція у = cos x спадає на відрізку [0; ?] і приймає всі значення від -1 до 1, тому рівняння cos x = а, |а| < 1 на проміжку [0; ?] має єдиний корінь, який називається арккосинусом числа а і позначається arccos a.
Арккосинусом числа а називається таке число з проміжку [0; ?], косинус якого дорівнює а.
Приклад 1. Знайдіть arccos  .
.
Arccos  =
=  , бо cos
, бо cos  =
=  i
i 
 [0;?].
[0;?].
Приклад 2. Знайдіть arccos 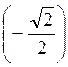 .
.
Arccos 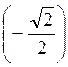 =
= 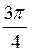 , бо cos
, бо cos 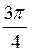 = –
= –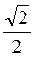 і
і 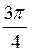
 [0;?].
[0;?].
Виконання вправ______________________________
1. Обчисліть:
A) arccos 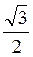 ; б) arccos
; б) arccos 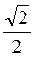 ; в) arccos 0; r) arccos (-1); д) arccos 1; є) arccos
; в) arccos 0; r) arccos (-1); д) arccos 1; є) arccos 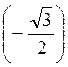 .
.
Відповідь: a)  ; б)
; б)  ; в)
; в)  ; г) ?; д) 0; є)
; г) ?; д) 0; є) 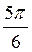 .
.
2. Які з поданих виразів мають смисл і чому:
A) arccos  ; б) arccos
; б) arccos 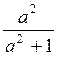 ; в) arccos
; в) arccos 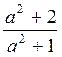 ; г) arccos
; г) arccos 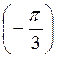 ; д) arccos
; д) arccos 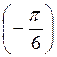 ; є) arccos
; є) arccos 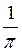 ?
?
Відповідь: б); д); е).
3. Знайдіть:
A) arccos 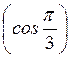 ; б) arccos
; б) arccos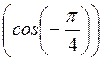 ; в) cos (arccos (-1)).
; в) cos (arccos (-1)).
Відповідь: a)  ; б)
; б)  ; в)-1.
; в)-1.
Аналогічно можна говорити про функцію у = arccos x. Графік функції у = arccos x одержимо із графіка функції у = cos x, x [0; ?] перетворенням симетрії відносно прямої у = х (рис. 115).
[0; ?] перетворенням симетрії відносно прямої у = х (рис. 115).
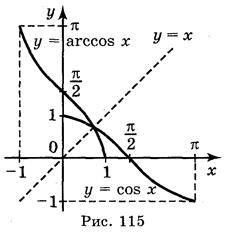
Розглянемо властивості функції у = arccos х.
1. D(y) = [-1; 1].
2. Е(y) = [0;?].
3. Графік не симетричний ні відносно початку координат, ні відносно осі OY. arccos (-х) = ? – arccos х.
4. Функція спадна. Якщо х1 > х2 то arccos х1 < arccos х2.
5. у = 0, якщо х = 1.
6. уmах = y(-1) = ?, ymіn = y(1) = 0.
Виконання вправ
1. Порівняйте числа:
A) arccos 0,1 і arccos 0,2; б) arccos 0,1 і arccos (-0,1); в) arccos (-0,2) і arccos (-0,3).
Відповідь: a) arccos 0,1 > arccos 0,2; б) arccos 0,1 < arccos (-0,1); в) arccos (-0,2) < arccos (-0,3).
2. Розташуйте числа в порядку зростання:
A) arccos 0,55; arccos 0,7; arccos 0,1;
Б) arccos (-0,3); arccos (-0,7); arccos (-0,9);
В) arccos 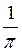 ; arccos (-0,3); arccos (-0,7).
; arccos (-0,3); arccos (-0,7).
Відповідь: a) arccos 0,7; arccos 0,55; arccos 0,1; б) arccos (-0,3); arccos (-0,7); arccos (-0,9); в) arccos 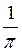 ; arccos (-0,3); arccos (-0,7).
; arccos (-0,3); arccos (-0,7).
3. Знайдіть область визначення функцій:
А) у = arccos (х – 1); б) у = arccos 2x; в) у = arccos (х2 + 1); г) у = arccos (|х| – 1).
Відповідь: а) х [0; 2]; б) х
[0; 2]; б) х [-0,5; 0,5]; в) х
[-0,5; 0,5]; в) х {0}; г) х
{0}; г) х [-2; 2].
[-2; 2].
4. Знайдіть область значень функцій: а) у = arccos |х|; б) у = arccos (-|х|).
Відповідь: а) у
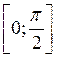 ; б) у
; б) у
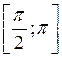 .
.
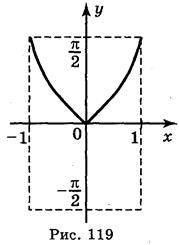
5. Побудуйте графіки функцій:
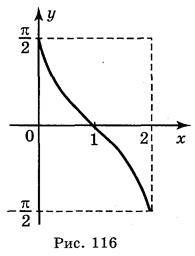
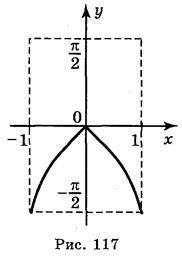
А) у = arccos(x – 1) –  ; б) у = arccos | х | –
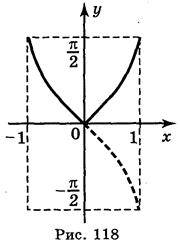
; б) у = arccos | х | –  ; в) у = ¦arccos х –
; в) у = ¦arccos х –  ¦; г) у = ¦arccos | х | –
¦; г) у = ¦arccos | х | –  ¦.
¦.
Відповідь: а) рис. 116; б) рис. 117; в) рис. 118; г) рис. 119.
IV. Підведення підсумку уроку
V. Домашнє завдання
Розділ II § 1 (2; 3). Запитання і завдання для повторення розділу II № 6; 7; 9; 10; 11; 12 (1, 2, 5, 6, 7, 8).
