ОДНОЧЛЕН. ДІЇ З ОДНОЧЛЕНАМИ
РОЗДІЛ II ОДНОЧЛЕНИ
&7. ОДНОЧЛЕН. ДІЇ З ОДНОЧЛЕНАМИ
Ви вже знаєте, що таке числовий вираз і вираз зі змінними, які вирази називають сумою, різницею, добутком, часткою, натуральним степенем чисел (чи змінних), які вирази відносяться до цілих виразів.
Запам’ятайте!
Цілий вираз, що є добутком чисел, змінних та їх натуральних степенів, називається одночленом.
Наприклад, кожен із добутків 5 ∙ 5, 32а, ху, 32аху, х2, 9 ∙(-x2) є одночленом.
Самі числа, змінні та їх натуральні степені також вважають одночленами. Наприклад, 5, -5, а, х2, –
? Чи можна вважати одночленом вираз 5 ∙  ? Ні, оскільки даний вираз не задовольняє означення одночлена.
? Ні, оскільки даний вираз не задовольняє означення одночлена.
З одночленами можна викопувати дії всіх трьох ступенів – додавання, віднімання, множення, ділення та піднесення до степеня. Розглянемо властивості цих дій.
1. Дії першого ступеня з одночленами
Додавання одночленів підкоряється переставному і сполучному законам.
Наприклад, 7х + ху = ху + 7х, (7х + ху) + 2 = = 7х + (ху + 2). Ці рівності є правильними для будь-яких значень змінних.
Якщо додають (чи віднімають) одночлени з однаковою
Задача 1. Чи можна подати у вигляді одночлена суму одночленів:
1)25x5y2 і 6,015х5y2;
2) 25x4y2 і 6,015х5y2?
Розв’язання. 1. Одночлени 25×5у2 і 6,015х5у2 мають ту саму буквену частину х5у2, тому в сумі ці доданки є подібними і їх можна звести:
25×5у2 + 6,015х5y2 = 31,015х5у2.
Отже, суму даних одночленів можна подати у вигляді одночлена.
2. Одночлени 25х4y2 і 6,015х5у2 мають різні буквені частини x4у2 і x5y2, тому в сумі ці доданки не є подібними і їх не можна звести.
Отже, суму даних одночленів не можна подати у вигляді одночлена.
Запам’ятайте!
Суму (чи різницю) одночленів можна подати у вигляді одночлена лише тоді, коли вони мають ту саму буквену частину.
Зверніть увагу:
Щоб подати у вигляді одночлена суму (чи різницю) одночленів:
1) з’ясуйте, чи є подібні доданки в даному виразі;
2) якщо всі доданки є подібними, то зведіть їх;
3) якщо подібних доданків немає або не всі доданки є подібними, то даний вираз не можна подати у вигляді одночлена.
2. Дії другого ступеня з одночленами
Множення одночленів підкоряється переставному і сполучному законам. Наприклад, 7х ∙ ху = ху ∙ 7х, (7х ∙ ху) ∙ 2 = 7х ∙ (ху ∙ 2). Ці рівності є правильними для будь-яких значень змінних.
Властивості ділення одночленів ви будете вивчати в курсі алгебри 8 класу.
? Чи можна добуток одночленів подати у вигляді одночлена? Так. Для цього користуються законами множення та основною властивістю степенів.
Задача 2. Знайдіть добуток одночленів -0,2х4у6 і 5аху2.
Розв’язання. Запишемо добуток усіх найпростіших одночленів, що входять до кожного із даних одночленів:
-0,2х4у6 ∙ 5аху2 =
=-0,2 ∙ х4 ∙ у6 ∙ 5 ∙ а ∙ х ∙ у2.
Застосувавши переставний і сполучний закони, згрупуємо числові множники та множники з відповідно однаковими змінними:
-0,2 ∙ x4 ∙ у6 ∙ 5 ∙ а ∙ х ∙ у2=
= (-0,2 ∙ 5) ∙ х4х ∙ у6у2 ∙ а.
Застосуємо основну властивість степеня та обчислимо добуток числових множників:
(-0,2 ∙ 5) а ∙ х4х ∙ у6у2 =
= -1 ∙ а ∙ х5 ∙ у8 = – ах5у8
Отже, -0,2 х4у6 ∙ 5аху2 = – ах5у8.
В одночленах числовий множник 1 не записують, а від числового множника -1 залишають тільки знак “-” перед буквеною частиною одночлена.
Розв’язавши задачу 2, ми знайшли добуток двох одночленів та спростили його. На першому місці в отриманому добутку стоїть числовий множник, а на наступних місцях – степені різних змінних. Такий вигляд одночлени називають стандартним. Наприклад, одночлени -0,2×2у6, 5аху2 і – ах5у8 є одночленами стандартного вигляду.
Зверніть увагу:
Будь-який одночлен можна записати в стандартному вигляді.
Якщо одночлен записано в стандартному вигляді, то числовий множник називають коефіцієнтом одночлени. Наприклад, одночлени -0,2х4у6, 5аху2 і – ах5у8а мають відповідно коефіцієнти -0,2, 5 і -1.
Запам’ятайте!
Степенем одночлена називається сума показників степенів змінних, що входять до нього.
Наприклад, степінь одночлена -0,2x4y6 дорівнює 10, оскільки показниками степенів змінних х і у є відповідно числа 4 і 6, сума яких дорівнює 10. Міркуючи аналогічно, дістанемо, що степінь одночлена 5аху2 дорівнює 4. Степінь одночлена – ах5у8 дорівнює 14.
Вважають, що будь-яке число, відмінне від нуля – це одночлен, степінь якого дорівнює нулю.
3. Дія третього ступеня з одночленами
Ви знаєте, що дія третього ступеня це дія піднесення до степеня. Одночлени також можна підносити до степеня, спираючись на властивості дій зі степенями. Розглянемо приклади.
Задача 3. Піднесіть до п’ятого степеня одночлен:
1) 2ху2; 2) – аx5y8.
Розв’язання.
1. (2ху2)5 = (2)5 ∙ х5 ∙ (y2)5 = 32х5у10.
2. (-ах5y8)5 = (-1)5 ∙ а5 ∙ (х5)5 ∙ (y8)5 = – а5х25у40.
Зверніть увагу:
Щоб піднести одночлен до n-го степеня, піднесіть до цього степеня кожний множник даного одночлена та обчисліть коефіцієнт отриманого одночлена.
Дізнайтеся більше
Творцем сучасної буквеної символіки вважають французького математика Франсуа Вієта (1540-1603). До XVI ст. математичні викладки велися в основному словесно. Наслідуючи приклад античних учених, Вієт чітко розмежував числа, величини та відношення, зібравши їх у деяку систему “видів”. Для цих видів Вієт запропонував спеціальну символіку, позначивши їх маленькими літерами латинської абетки. Для невідомих величин застосовувалися голосні літери, для змінних – приголосні. Вієт показав, що, оперуючи символами, можна розв’язати задачу в загальному вигляді. Це поклало початок докорінних змін у розвитку алгебри: стали можливими символьні обчислення. Не випадково, що за це Вієта називають “батьком” алгебри, основоположником буквеної символіки.

ПРИГАДАЙТЕ ГОЛОВНЕ
1. Що таке одночлен?
2. Що означає – додати одночлени?
3. Як додають (віднімають) одночлени з однаковою буквеною частиною?
4. Чи можна добуток одночленів подати у вигляді одночлена?
5. Який вигляд одночлена називають стандартним?
6. Що називають коефіцієнтом одночлена; степенем одночлена? Як обчислити степінь одночлена?
7. Як піднести одночлен до степеня?
РОЗВ’ЯЖІТЬ ЗАДАЧІ
324. Чи може бути одночленом вираз, що містить дію:
1) додавання; 4) ділення на змінну;
2) віднімання; 5) ділення на число;
3) множення; 6) піднесення до степеня?
325. Які з даних одночленів є найпростішими:
1) ху, 2)-112; 3 )k2а6; 4)b5; 5)  А; 6)0,32m; 7)-3nх, 8)2у?
А; 6)0,32m; 7)-3nх, 8)2у?
326. Чи можна подати у вигляді одночлена суму:
1) а + b + 3а + (-b); 2)а + а + (-3а); 3)6х + 4 + 12х?
327. Який із даних виразів є добутком одночленів -5у і 4х2:
1) – х2у, 2)-2х2у 3)-20x2y?
328. Чи є даний вираз одночленом стандартного вигляду:
1)х; 2) х ∙ 8; 3)3х2х; 4)-7х ∙ 9у; 5) х + у; 6)-2ух2?
Якщо так, то який у нього коефіцієнт?
329. Чи правильно, що степінь одночлена 7nm2р2 дорівнює:
1)7; 2)4; 3)2; 4)5?
330. Які помилки допущено при піднесенні одночлена до квадрата:
1) (0,2а)2 = 0,4a2; 3) (-3xy)2 = -9x2y2;
2) (5ab3)2 = 5a2b5; 4) (2 B5a7)2 = 4
B5a7)2 = 4 B10a2?
B10a2?
331. Чи можна подати у вигляді одночлена суму одночленів:
1) 34ху2 і 1 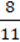 Ху2;
Ху2;
2) 4,6х9у2 і 4,6x8y2;
3) 3543а і 4,6?
332. Чи є даний вираз одночленом:
1) а3;
2) а2 ∙ 356;
3) x2y3z12;
4) -3х : у;
5) х + х;
6) -2(а + b2);
7) 2 – bа;
8) 1; 9) 0; 10) 43; 11) 2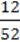 ;
;
12) ( )2; 13) (
)2; 13) ( )4?
)4?
333. Запишіть суму одночленів та спростіть її, якщо можна:
1) 10,1хy2 і 6,9xy2; 4) -4а і 2а;
2) 0,125х і -0,125х2; 5) 3n3m2 і – m3n2;
3) 10ab i -3ab; 6) -6x і 9.
334. Запишіть різницю одночленів та спростіть її:
1) 10,1 ху і 6,9хy;
2) 5  Х4 і 0,4х4;
Х4 і 0,4х4;
3) 10a6 i 3ba;
4)-46а і 2а.
335. Подайте одночлен у вигляді добутку найпростіших одночленів:
1) 0,25ху16;
2) -7  Хуz2;
Хуz2;
3) 55а10b5;
4) abху2;
5) 2z10х16у2.
336. Знайдіть добуток одночленів:
1) 2х і ху; 5) 2  а3с4 і 3а4;
а3с4 і 3а4;
2)5mn і 3mn; 6) -10аb2 і -3b;
3) – ab2і а2b; 7) 0,5m3n6 i 0,08m6n3;
4) 7,2х4 і  х5у; 8)-1,2асb і
х5у; 8)-1,2асb і  Хуz.
Хуz.
337. Знайдіть добуток одночлена 10a3c4b5 і одночлена:
1) 1,6ху;
2) 2  A3c4b5;
A3c4b5;
3) -10ab2 ;
4) -3b;
5) 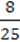 ac6b14;
ac6b14;
6) 3a4x4.
338. Який із одночленів записано в стандартному вигляді:
1) -6; 2) b ∙ 9; 3)2k2 ∙ 3 ∙ l; 4)a8 ∙ a5; 5) 9,37a?
339. Зведіть до стандартного вигляду одночлен:
1) -0,5 ∙ х10 ∙ 26у2; 4) а4 ∙ 0,5 ∙ b8 ∙ а2 ∙ 40 ∙ b2;
2) 4 ∙ а ∙ у ∙ 0,1 ∙ а ∙ у9; 5)-0,125 ∙ х7 ∙у7 ∙ 16 ∙ х ∙ у2;
3)  ∙ а3 ∙ b5 ∙ а3 ∙ а3; 6) 6 ∙ а4 ∙ b10 ∙ а ∙ с10 ∙
∙ а3 ∙ b5 ∙ а3 ∙ а3; 6) 6 ∙ а4 ∙ b10 ∙ а ∙ с10 ∙  ∙ а6 ∙ (-9).
∙ а6 ∙ (-9).
340. Зведіть до стандартного вигляду одночлен:
1) -0,01 ∙ х ∙ х3 ∙ x6 ∙ 50; 3) х2 ∙ 5,4 ∙ y4 ∙  ∙ y ∙ (-0,8) ∙ x;
∙ y ∙ (-0,8) ∙ x;
2) у ∙ х ∙ 2 ∙ х ∙ у16 ∙ 40; 4) а10 ∙ 0,02 ∙ b45 ∙ а25 ∙ а56 ∙ b43 ∙ а9 ∙ b12.
341. Який степінь має одночлен:
1) 56ху;
2) – ;
;
3) k32l18;
4) а6b5;
5) 0,32а;
6) -4abcpxy?
Назвіть коефіцієнт одночлена.
342. Який степінь має одночлен:
1) – хуz;
2) 0,001;
3) 4p2m46;
4) а88сb;
5) 7,9х;
6) -1  а3b3?
а3b3?
Назвіть коефіцієнт одночлена.
343. Піднесіть одночлен х5zy2 до степеня n, якщо n дорівнює:
1)2; 2)8; 3)30.
344. Піднесіть до четвертого степеня одночлен:
1)-2x5y2;
2)0,01х6y8;
3) 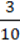 а5рb65с.
а5рb65с.
345. Знайдіть куб одночлена:
1) -0,2×21у32;
2)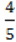 ху;
ху;
3)4а3с4b5.
346. Якими даними треба доповнити порожні клітинки таблиці 5?
Таблиця 5
Одночлен | -ху | 0,26 а2 | A | 1,75b | -7х | 81y | 0,5а2 |
Одночлен | |||||||
Сума Одночленів | Ху | 0 | 21а | -b |
| 0 | 1 |
347. Знайдіть значення виразу b – 4 а3b2 + (-2b)2aa2 + 3b, якщо:
1)а = 2,172, b = -1; 2) а = –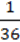 , b = –
, b = – .
.
348. Знайдіть одночлен, квадрат якого дорівнює:
1) 16а8b14;
2) 1 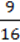 Х6у8;
Х6у8;
3) 0,0001 a100c40b50.
Скільки розв’язків має задача?
349. Подайте одночлен 21хmа3с4 у вигляді добутку двох одночленів, один з яких:
1)-7са; 2) 1,2 ma2.
350. Подайте одночлен ха3у вигляді добутку:
1) трьох одночленів стандартного вигляду;
2) чотирьох одночленів стандартного вигляду.
351. Якими даними треба доповнити порожні клітинки таблиці 6?
Таблиця 6
Одночлен | -ху | 0,26а2 | 0,2а | -1,25 b5a2 | -4ха2 | 0,5а2 |
Одночлен | ||||||
Добуток Одночленів | 4×2 = y | 26а3 | 0,5а6с5 | -b10а4 | А2х2 |
|
352. Піднесіть до п’ятого степеня одночлен:
1)2(хy5)8;
2)-0,1 p7(m8)2n;
3)1  B(b2a)6.
B(b2a)6.
353. Який степінь має одночлен:
1)-6((y6)5)3 ∙ (y8)6)2;
2) х6 ∙ х6 – х3;
3) (2у3)5 ∙ ((3у)2)2;
4) k2l6mpa4b5?
Назвіть коефіцієнт одночлена.
354. Спростіть вираз:
1) 2 ∙ (а2)3 ∙ (а2)2 – (5а5)2 + (а2)4 ∙ 63 ∙ а2;
2) 23 ∙ х2 ∙ у32 ∙ 53 ∙ х31 ∙ 0,0001 ∙ у2;
3) (bа3 ∙ bc3) – (аb2 – ас2).
355. Знайдіть значення виразу (а2)1 ∙ (а1)2 ∙ (а2)3 ∙ (а2)3 – а16, якщо:
1)а =34  ; 2) а = -0,000001.
; 2) а = -0,000001.
356. Зведіть одночлени до стандартного вигляду та знайдіть їх добуток:
1) 0,24х4y16, 5z2ху2 і 2z10x15y2;
2) 2 (y6)5 ∙ (x8)2, -0,8zxy9 i –
(y6)5 ∙ (x8)2, -0,8zxy9 i – Z12y;
Z12y;
3) 0,4х4y21, -1,5z5(-x) ∙ (-у)4 і 0,02(-z)6x15y2.
357. Сторона квадрата чисельно дорівнює потроєному об’єму куба з ребром а см. Знайдіть площу квадрата.
358. Сторону a квадрата збільшили в чотири рази, а потім збільшили ще в 1 рази. На скільки збільшилася площа квадрата?
рази. На скільки збільшилася площа квадрата?
359. Сторону квадрата а зменшили на 10 %, а потім ще на 20 %. Знайдіть периметр отриманого квадрата.
360. Подайте одночлен 0,08х11у5 у вигляді добутку двох одночленів, степінь одного з яких дорівнює:
1) 4; 2) 10; 3) 0.
361. Подайте одночлен – ху2у вигляді суми двох одночленів, коефіцієнт одного з яких дорівнює:
1) 4; 2) 0,25; 3)  .
.
Розгляньте різні випадки.
362. Визначте знак одночлена:
1) (-b200)301 ∙ ((-b)515)24, якщо b < 0;
2) (-а)1001 ∙ (-2а ∙ (-с)15)5, якщо а < 0, с > 0.
363. Знайдіть значення змінних х і у, за яких сума одночленів -(x2)2 ∙ | (-y3)4|3 і (ху9)4 дорівнює 0.
364. Знайдіть натуральні значення n, за яких рівність є правильною:
1) (b2 ∙ а5 ∙ an)2n = (ba5)20;
2) а2 ∙ b2 ∙ а8n ∙ a2n = b ∙ а8 ∙ b ∙ а8 ∙ (а8)2.
365. Спростіть вираз:
1) (2ban+1 ∙ 5bnban+1)2; 3 ) an+1 ∙ an+6 ∙ b ∙ (2аn+1 )3 ∙ аn.
2) (-2b)3 – (-x3)2n –  х3nb5.
х3nb5.
Знайдіть степінь і коефіцієнт одночлена.
366. Знайдіть значення виразу (аn+1∙ bnban+3)2 ∙ (а(bа)n+1)6, якщо an+2 = 2, b4(n+1) = 0,5.
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
367. Початкову ціну а грн за 1 альбом знизили спочатку на 10 %, а потім ще на 10 %. На скільки менше коштують с альбомів після знижки?
368. Сторона квадрата дорівнює и. Кожну сторону поділили на три рівні частини. На середніх частинах побудували квадрати (мал. 5). Кожні три сторони отриманих квадратів поділили на три частини і на середніх частинах побудували нові квадрати (мал. 6). Знайдіть площу отриманої фігури.
ЗАДАЧІ НА ПОВТОРЕННЯ
369. Розв’яжіть рівняння:
1) 6,9 – 2 ∙ (0,4 + х) = 0,5х +1,1;
2) 2,4х – 1,1(х – 2) = 3.
370. На свято придбали 36 кг цукерок трьох видів у відношенні 2 : 3 : 4. Скільки кілограмів цукерок кожного виду купили?
371. На координатній прямій позначте точки, координати яких є цілими числами, більшими за -2 і меншими від 10.
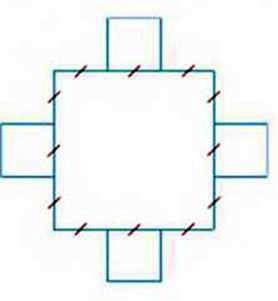
Мал. 5
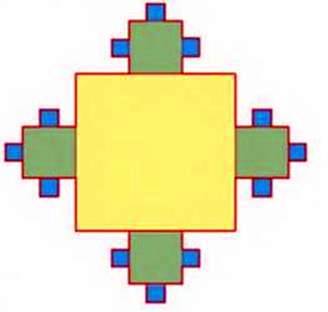
Мал. 6
ПЕРЕВІРТЕ, ЯК ЗАСВОЇЛИ МАТЕРІАЛ
КОНТРОЛЬНІ ЗАПИТАННЯ
1. Що таке степінь числа; основа степеня; показник степеня?
2. Що означає піднести число а до степеня n?
3. Чому дорівнює а в степені 1; 1 у степені n?
4 Який порядок виконання дій у виразі, що містить степені?
5. Які дії зі степенями можна виконувати?
6. Яка основна властивість степеня? Доведіть її.
7. Сформулюйте і доведіть властивість частки степенів з рівними основами.
8. Сформулюйте і доведіть властивість добутку (частки) степенів із різними основами і рівними показниками.
9. Яка властивість піднесення степеня до степеня? Доведіть її.
10. Що таке одночлен?
11. Чи можна добуток одночленів подати у вигляді одночлена?
12. Який вигляд одночлена називають стандартним?
13. Що таке коефіцієнт одночлена?
14. Що називають степенем одночлена?
15. Як піднести одночлен до степеня?
ТЕСТОВІ ЗАВДАННЯ
Уважно прочитайте задачі і знайдіть серед запропонованих відповідей правильну. Для виконання тестового завдання потрібно 10-15 хв.
1. Порівняйте: – 243 і (- 24 )3.
А. -243 > (-24)3. В. -243 = (-24)3.
Б. -243 < (-24)3. Г. Не можна визначити.
2 . Який із виразів є одночленом стандартного вигляду?
А. 9,51.
Б. а + b.
В. а3 ∙ а5.
Г.  .
.
3 . Квадрат якого з одночленів, даних у відповідях, дорівнює 64а4c16?
А. 64a2с8.
Б.-8а2с8.
В. 8а2с4.
Г. 8а4с16.
4. Знайдіть добуток одночленів 0,5(у6)3 і (2у8)5.
А. у22.
Б. 5у58
В. 16у58.
Г. 8у22.
5. Подайте у вигляді одночлена вираз 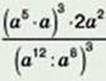 (а ≠ 0).
(а ≠ 0).
А. 4а8.
Б. 2а8.
В. 2a5.
Г.4а11.
