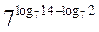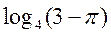Основні властивості логарифмів
УРОК 54
Тема. Основні властивості логарифмів
Мета уроку. Вивчення основних властивостей логарифмів. Познайомити учнів з логарифмуванням і потенціюванням виразів.
І. Перевірка домашнього завдання
1. Три учні відтворюють розв’язування вправ № 4, 6, 18.
2. Усне розв’язування вправ на обчислення логарифмів з використанням таблиці 22 для усних обчислень.
Таблиця 22
1 | 2 | 3 | 4 | 5 | |
1 | Log28 | Log39 | Log464 | Log5l25 | Log636 |
2 | Log | Log | Log | Log42 | Log93 |
3 |
|
|
|
| Log813 |
4 |
|
|
|
|
|
5 |
|
|
|
|
|
3. Відповіді на запитання, що виникли в учнів під час виконання домашнього завдання.
II. Сприймання і усвідомлення основних властивостей логарифмів
При виконанні перетворень виразів, які містять логарифми, при обчисленнях і при розв’язуванні рівнянь, нерівностей часто використовуються властивості логарифмів.
Для будь-яких а > 0, а? 1 і будь-яких додатних х і у виконуються рівності:
1. logа l = 0;
2. logаa = 1;
3. logа xy = logа x + logа y;
4. logа 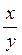 = logа x – logа y;
= logа x – logа y;
5. logа х р = p logа x (р 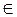 R);
R);
6. 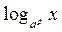 =
= 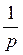 loga x (p
loga x (p 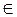 R);
R);
7. loga x = 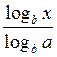 (b > 0, b? 1).
(b > 0, b? 1).
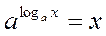 (І)
(І)
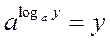 (II)
(II)
Перемноживши рівності (І) і (II), одержуємо: ху = 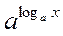 –
– 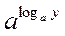 =
= 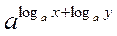 ,
,
Звідси за означенням логарифма маємо loga xy = loga x + loga y.
Отже, логарифм добутку дорівнює сумі логарифмів.
Розділивши рівності (І) і (II), одержуємо: 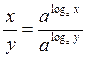 =
= 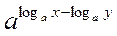 ,
,
Звідси за означенням логарифма маємо: loga 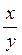 = loga х – loga у.
= loga х – loga у.
Отже, логарифм частки дорівнює різниці логарифмів.
Піднісши ліву і праву частини рівності (І) до степеня з показником р, маємо: 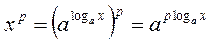 (ІІІ)
(ІІІ)
Звідси за означенням логарифма маємо: logа х р = p logа x.
Отже, логарифм степеня дорівнює добутку показника степеня на логарифм основи цього степеня.
З рівності (III) маємо: 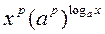 , звідси за означенням логарифма маємо:
, звідси за означенням логарифма маємо:
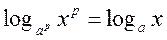 , тоді p
, тоді p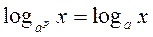 ;
; 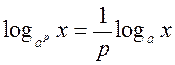 .
.
Формула 7 називається формулою переходу від одної основи логарифма до другої основи. Доведемо її.
За правилом логарифмування степеня (формула 5) та основною логарифмічною тотожністю одержуємо: 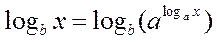 ,
,
Звідси logb х = loga х – logb a або loga = 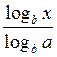 .
.
За допомогою формули 7 можна знаходити логарифми з довільною основою а, маючи таблиці логарифмів, складених для якої-небудь основи b. Найбільш вживаними є таблиці десяткових і натуральних логарифмів.
III. Осмислення основних властивостей логарифмів
1. Розглянемо приклади використання формул 3-7. Обчислимо:
1) log6 18 + log6 2 = log6(18 – 2) = log6 36 = 2;
2) log12 48 – log12 4 = log6 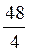 = log12 12 = 1;
= log12 12 = 1;
3) log6  = log6
= log6 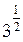 =
=  Log6 3 =
Log6 3 =  – 1 =
– 1 =  ;
;
4) log125 5 = log125 5 = 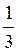 Log5 5 =
Log5 5 = 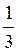 – 1 =
– 1 = 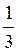 ;
;
5) 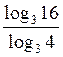 = log4 16 = log4 42 = 2 log4 4 = 2 – 1 = 2.
= log4 16 = log4 42 = 2 log4 4 = 2 – 1 = 2.
2. Використовуючи калькулятор (або таблиці), обчислимо:
1) log3 2 = 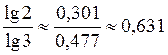 ;
;
2) log3 2 = 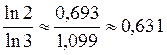 .
.
3. Виконання вправ № 29, 30.
IV. Сприймання і усвідомлення логарифмування і потенціювання виразів
Дія знаходження логарифма числа (виразу) називається логарифмуванням.
Приклад. Прологарифмуйте вираз у = 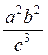 .
.
Розв’язання
Lg y = lg 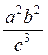 = lg (a2b2) – lg c3 = lg a2 + lg b2 – lg c3 = 2 lga + 2 lg b – 3 lg c.
= lg (a2b2) – lg c3 = lg a2 + lg b2 – lg c3 = 2 lga + 2 lg b – 3 lg c.
Дія, обернена до логарифмування, називається потенціюванням.
Потенціювання – знаходження числа (виразу) за його логарифмом.
Приклад. Пропотенціюйте вираз lg х =  lg 5а – 3 lg b + 4 lg c.
lg 5а – 3 lg b + 4 lg c.
Розв’язання
Lg x =  lg 5a – 3 lg b + 4 lg c;
lg 5a – 3 lg b + 4 lg c;
Lg x = lg 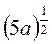 – lg b3 + lg c4;
– lg b3 + lg c4;
Lg x = lg 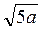 – lg b3 + lg c4; lg x = lg (
– lg b3 + lg c4; lg x = lg (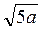 – с4) – lg b3;
– с4) – lg b3;
Lg x = lg 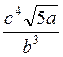 ; x =
; x = 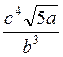 .
.
Виконання вправ № 24 (4), 31 (4).
V. Підведення підсумків уроку
VI. Домашнє завдання
Розділ V § 1. Запитання і завдання для повторення № 6-14. Вправи № 24 (2), 27, 28, 31 (3).
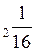
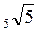
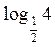
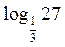
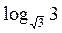
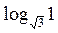
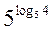
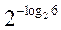
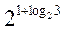
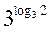 – 1
– 1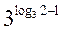
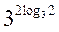
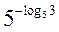
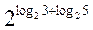 class=""/>
class=""/>