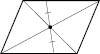
Паралелограм
Геометрія
Чотирикутники
Чотирикутником називається фігура, яка складається з чотирьох точок і чотирьох відрізків, що послідовно їх сполучають. При цьому жодні три з даних точок не повинні лежати на одній прямій, а відрізки, які їх сполучають, не повинні перетинатися. Дані точки називаються Вершинами чотирикутника, а відрізки, що їх сполучають,- Сторонами чотирикутника.
Вершини чотирикутника називаються Сусідніми, якщо вони є кінцями однієї з його сторін. Несусідні вершини називаються Протилежними. Відрізки, що сполучають протилежні
Сторони чотирикутника, що виходять з однієї вершини, називаються Сусідніми сторонами. Сторони, які не мають спільного кінця, називаються Протилежними сторонами.
Периметр Чотирикутника – сума довжин усіх його сторін.
Чотирикутник називається Опуклим, якщо він лежить в одній півплощині відносно будь-якої прямої, що містить його сторону.
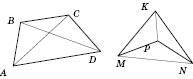
На рисунку нижче зліва ABCD – опуклий чотирикутник; AC, BD – його діагоналі. На рисунку справа KMNP – неопуклий чотирикутник; KN, MP – його діагоналі.
Сума кутів чотирикутника
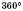.Паралелограм
Паралелограм – це чотирикутник, у якого протилежні сторони паралельні.
На рисунку ABCD – паралелограм.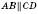 
; 
.
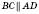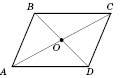
Властивості паралелограма
Теорема 1. У паралелограма протилежні сторони рівні: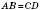 
, 
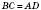(дивись вищенаведений рисунок). У паралелограма протилежні кути рівні: 
, 
.
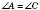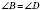Теорема 2. У паралелограмі кути, прилеглі до однієї сторони, в сумі дорівнюють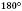 
:
; 
;
; 
.
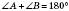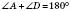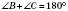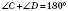Теорема 3. Діагоналі паралелограма перетинаються й у точці перетину діляться навпіл.
; 
.
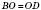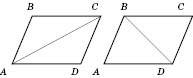
Теорема 4. Діагональ паралелограма поділяє його на два рівні трикутники.
На рисунку нижче зліва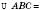 
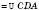. На рисунку справа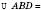 
.
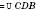Теорема 5. Діагоналі паралелограма розбивають його на дві пари рівних трикутників.
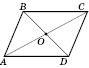
На рисунку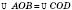 
; 
.
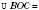
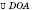Ознаки паралелограма
Теорема 1. Якщо діагоналі чотирикутника перетинаються й у точці перетину діляться навпіл, то цей чотирикутник – паралелограм.
Теорема 2. Якщо в чотирикутнику дві сторони паралельні й рівні, то цей чотирикутник – паралелограм.
Теорема 3. Якщо в чотирикутнику протилежні сторони рівні, то цей чотирикутник – паралелограм.
Теорема 4. Якщо в чотирикутнику протилежні кути рівні, то цей чотирикутник – паралелограм.
Теорема 5. Якщо в чотирикутнику кути, що є прилеглими до кожної із сторін, у сумі дорівнюють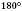 
, то цей чотирикутник – паралелограм.
Теорема 6. Якщо кожна діагональ поділяє чотирикутник на два рівні трикутники, то цей чотирикутник – паралелограм.
Кут між висотами паралелограма
Висота паралелограма – це відрізок, перпендикулярний до протилежних сторін паралелограма з кінцями на цих сторонах.
На рисунку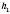 
і 
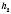– висоти паралелограмa.
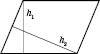
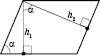
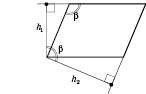
Найчастіше висоти опускають із вершин паралелограма. Із кожної вершини паралелограма можна провести дві висоти. Кут між ними дорівнюватиме куту паралелограма при сусідній вершині. На рисунку внизу зліва зображений кут між висотами паралелограма, опущеними з тупого кута, на рисунку справа – між висотами, опущеними з гострого кута:
Властивості бісектрис кутів паралелограма
1. Бісектриси сусідніх кутів паралелограма перпендикулярні.
2. Бісектриси протилежних кутів паралелограма паралельні або збігаються (якщо паралелограм – ромб).
3. Бісектриса кута паралелограма відокремлює від нього рівнобедрений трикутник.
На рисунку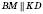 
; 
; 
; 
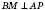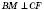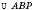– рівнобедрений;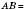 
; 
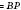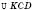– рівнобедрений, 
.
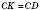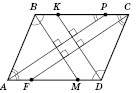
Чотирикутник, що утворився при перетині бісектрис кутів паралелограма,- прямокутник. Якщо через точку перетину діагоналей паралелограма проведено пряму, то відрізок цієї прямої, який розташований між паралельними сторонами, ділиться в цій точці навпіл:
(2 votes, average: 5.00 out of 5)
Loading...