Головна ⇒ 📌Довідник с фізики ⇒ Принцип відносності Галілея

Принцип відносності Галілея

ФІЗИКА

Частина 1 МЕХАНІКА

Розділ 2 ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ

2.4. Принцип відносності Галілея

Розглянемо дві системи відліку К і К’ (рис. 2.1). Нехай система К’ рухається відносно системи К уздовж осі х зі швидкістю υ0. Тоді можна записати зв’язок між координатами матеріальної точки А для цих систем:

Принцип відносності Галілея

Перші дві координати точки збігаються тому, що обмежено рух системи К’ лише вздовж осі х. Отже, з часом змінюється тільки ця координата. Проте в загальному випадку змінюватимуться всі координати.

Плинність часу в обох системах однакова.

Принцип відносності Галілея

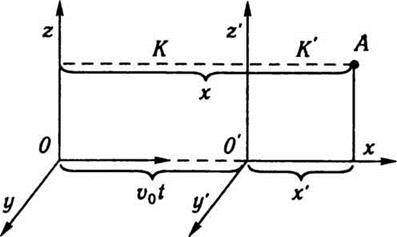
Рис. 2.1.

Формули (2.1) називають перетвореннями Галілея. Якщо від перших трьох рівнянь (2.1) візьмемо похідні за часом, то дістанемо відповідні проекції швидкостей 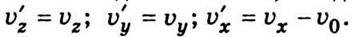Принцип відносності Галілея Ці співвідношення можна записати у векторній формі:

Принцип відносності Галілея

Швидкість Принцип відносності Галілея відносно нерухомої системи відліку К складається із швидкості Принцип відносності Галілея‘ відносно рухомої системи К’ і швидкості Принцип відносності Галілея0 системи К’ відносно системи К. Формулу (2.2) називають законом додавання

швидкостей.

Візьмемо похідну за часом від лівої та правої частин рівності (2.2). Враховуючи, що Принцип відносності Галілея0 є величина стала, дістанемо

Принцип відносності Галілея

Тобто в усіх інерційних системах прискорення залишається сталим.

Взагалі абсолютної системи відліку не існує, а поняття абсолютного спокою позбавлене сенсу. Якщо тіло перебуває в стані спокою в одній із інерційних систем відліку, то відносно всіх інших воно рухатиметься з різними сталими швидкостями, тому немає підстав віддавати перевагу одній системі перед іншими. У класичній механіці немає поняття абсолютної швидкості, тільки відносна швидкість тіл має фізичний зміст. Водночас поняття абсолютного прискорення справедливе, оскільки воно в різних інерційних системах відліку однакове.

Як видно із співвідношення (2.3), рівняння динаміки не змінюються, якщо перейти від однієї інерційної системи відліку до іншої, тобто вони інваріантні щодо перетворень Галілея. З погляду механіки всі інерційні системи відліку абсолютно еквівалентні: жодній з них не можна віддавати перевагу перед іншими. Практично це виявляється у тому, що ніякими механічними дослідами, проведеними в цій системі відліку, не можна встановити, перебуває вона в стані спокою чи в стані рівномірного і прямолінійного руху.

Такі властивості інерційних систем вперше з’ясував Галілей. Принцип відносності Галілея можна сформулювати так: усі механічні явища в різних інерційних системах відліку відбуваються однаково, внаслідок чого ніякими механічними дослідами неможливо встановити, нерухома ця система чи рухається рівномірно і прямолінійно.


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. ПОСТУЛАТИ СУЧАСНОЇ ТЕОРІЇ ВІДНОСНОСТІ. ПЕРЕТВОРЕННЯ ЛОРЕНЦА Фізика підготовка до ЗНО комплексне видання КВАНТОВА ФІЗИКА. ЕЛЕМЕНТИ ТЕОРІЇ ВІДНОСНОСТІ 1. ЕЛЕМЕНТИ ТЕОРІЇ ВІДНОСНОСТІ 1.2. ПОСТУЛАТИ СУЧАСНОЇ ТЕОРІЇ ВІДНОСНОСТІ. ПЕРЕТВОРЕННЯ ЛОРЕНЦА 1. Усі закони фізики в усіх інерційних системах відліку однакові (принцип відносності Ейнштейна). 2. Швидкість світла у вакуумі (с) не залежить від швидкості руху джерела, тобто с однакова в усіх інерційних системах відліку […]...

  2. ПРИНЦИП ВІДНОСНОСТІ В КЛАСИЧНІЙ МЕХАНІЦІ – ПРИНЦИП ВІДНОСНОСТІ ГАЛІЛЕЯ Фізика підготовка до ЗНО комплексне видання МЕХАНІКА 2. ОСНОВИ ДИНАМІКИ 2.1. ОСНОВНІ ЗАКОНИ ДИНАМІКИ. СИЛА. РІВНОДIЙНА СИЛА 2.1.2. ПРИНЦИП ВІДНОСНОСТІ В КЛАСИЧНІЙ МЕХАНІЦІ (ПРИНЦИП ВІДНОСНОСТІ ГАЛІЛЕЯ) Принцип відносності в класичній механіці: для будь-яких механічних явищ усі інерціальні СВ є рівноправними. Це зумовлено тим, що маса т, довжина l, проміжок часу Δt в усіх інерціальних СВ […]...

  3. Основні положення спеціальної теорії відносності ФІЗИКА Частина 4 ОПТИКА. СПЕЦІАЛЬНА ТЕОРІЯ ВІДНОСНОСТІ Розділ 14 ШВИДКІСТЬ ПОШИРЕННЯ СВІТЛА. ОСНОВИ СПЕЦІАЛЬНОЇ ТЕОРІЇ ВІДНОСНОСТІ 14.7. Основні положення спеціальної теорії відносності Наприкінці XIX ст. фізикам здавалось, що наступні дослідження тільки доповнюватимуть наші знання, а фундаментальних змін не відбудеться. Всю цю струнку й непорушну ззовні “споруду” тепер називають класичною фізикою. Загальну гармонію фізики порушували лише […]...

  4. Динаміка спеціальної теорії відносності ФІЗИКА Частина 4 ОПТИКА. СПЕЦІАЛЬНА ТЕОРІЯ ВІДНОСНОСТІ Розділ 14 ШВИДКІСТЬ ПОШИРЕННЯ СВІТЛА. ОСНОВИ СПЕЦІАЛЬНОЇ ТЕОРІЇ ВІДНОСНОСТІ 14.8. Динаміка спеціальної теорії відносності Ми розглянули винятково просторово-часові співвідношення, кінематику теорії відносності. Тепер ознайомимося з релятивістською динамікою. Мірою взаємодії одного тіла з іншим є сила. Маса тіла вводиться як індивідуальна стала характеристика, що вимірюється інертністю тіла. Важливим етапом […]...

  5. Динаміка 5. Механіка 5.2. Динаміка Динаміка – це розділ механіки, в якому вивчається рух тіл під дією прикладених до них сил. Інерція – це явище збереження швидкості тіла після того, як на нього перестають діяти інші тіла. Інерціальна система відліку – це геліоцентрична система відліку, що рухається рівномірно і прямолінійно в просторі. Будь-яка система відліку, яка […]...

  6. Основні положення спеціальної теорії відносності. Швидкість світла у вакуумі як гранично допустима швидкість передавання взаємодії РЕЛЯТИВІСТСЬКА МЕХАНІКА Урок № 1 Тема. Основні положення спеціальної теорії відносності. Швидкість світла у вакуумі як гранично допустима швидкість передавання взаємодії Мета: повторити принцип відносності Галілея та ознайомити учнів із передумовами виникнення теорії відносності, сформулювати в учнів розуміння основних положень; розвивати логічне мислення, вміння аналізувати, робити висновки; формувати в учнів усвідомлення пізнаваності навколишнього світу і […]...

  7. Основні наслідки, що випливають із постулатів теорії відносності 2-й семестр МЕХАНІКА 5 . Релятивістська механіка Урок 3/70 Тема. Основні наслідки, що випливають із постулатів теорії відносності Мета уроку: ознайомити учнів з найважливішими наслідками, що стосуються властивостей простору й часу Тип уроку: вивчення нового матеріалу План уроку Контроль знань 5 хв. 1. Класичний закон додавання швидкостей. 2. Релятивістський закон додавання швидкостей. 3. Одночасність подій […]...

  8. Основні наслідки спеціальної теорії відносності РЕЛЯТИВІСТСЬКА МЕХАНІКА Урок № 2 Тема. Основні наслідки спеціальної теорії відносності Мета: з’ясувати відносність одночасності подій у різних ІСВ, відносність часу та відстаней; розвивати логічне мислення, вміння проводити уявний експеримент, робити висновки. Тип уроку: урок вивчення нового матеріалу. ХІД УРОКУ I. Актуалізація опорних знань Фізичний диктант 1. У 1905 році Ейнштейн створив теорію… 2. В […]...

  9. Філософське значення теорії відносності ФІЗИКА Частина 4 ОПТИКА. СПЕЦІАЛЬНА ТЕОРІЯ ВІДНОСНОСТІ Розділ 14 ШВИДКІСТЬ ПОШИРЕННЯ СВІТЛА. ОСНОВИ СПЕЦІАЛЬНОЇ ТЕОРІЇ ВІДНОСНОСТІ 14.12. Філософське значення теорії відносності Теорія відносності тісно пов’язана з філософією. Насамперед слід зазначити, що основою її створення став глибокий філософський аналіз А. Ейнштейном понять простору і часу. Крім того, перегляд теорією відносності просторово-часових уявлень, що панували в класичній […]...

  10. Перетворення Лоренца ФІЗИКА Частина 4 ОПТИКА. СПЕЦІАЛЬНА ТЕОРІЯ ВІДНОСНОСТІ Розділ 14 ШВИДКІСТЬ ПОШИРЕННЯ СВІТЛА. ОСНОВИ СПЕЦІАЛЬНОЇ ТЕОРІЇ ВІДНОСНОСТІ 14.5. Перетворення Лоренца Розвиваючи свою гіпотезу, X. Лоренц показав, що для подолання суперечностей, які виникли при поясненні досліду Майкельсона та інших, треба ввести нові рівняння для перетворення координат при переході від системи координат, що перебуває в стані спокою, до […]...

  11. ВІДНОСНІСТЬ ОДНОЧАСНОСТІ – ВИСНОВКИ СТВ Фізика підготовка до ЗНО комплексне видання КВАНТОВА ФІЗИКА. ЕЛЕМЕНТИ ТЕОРІЇ ВІДНОСНОСТІ 1. ЕЛЕМЕНТИ ТЕОРІЇ ВІДНОСНОСТІ 1.3. ВИСНОВКИ СТВ 1.3.3. ВІДНОСНІСТЬ ОДНОЧАСНОСТІ Події, одночасні в одній інерційній системі відліку, не одночасні в інших інерційних системах, рухомих відносно першої. Розрізняють події просторово-часові і причинно-наслідкові. Якщо подія причинно-наслідкова, то неможлива система відліку, в якій наслідкова подія випередила б […]...

  12. ПОДОРОЖ У ТЕОРІЮ ВІДНОСНОСТІ “ПОДОРОЖ У ТЕОРІЮ ВІДНОСНОСТІ” Урок-подорож Мета. Сформувати в учнів усвідомлення пізнаванності навколишнього світу і безмежності пізнання; встановити зв’язки мікро – і макросвіту на основі розгляду застосування теорії відносності в астрономії й атомній фізиці. Тип уроку. Урок узагальнення і систематизації знань. Обладнання. Портрети Г. Галілея, І. Ньютона, А. Ейнштейна; плакат з уривком із вірша: І в […]...

  13. Відносність руху – Кінематика 5. Механіка 5.1. Кінематика 5.1.11. Відносність руху Відносний рух – це рух матеріальної точки відносно рухомої системи відліку, яка певним чином переміщається відносно іншої, умовно прийнятої за нерухому. Формули додавання переміщень Переміщення тіла відносно нерухомої системи координат дорівнює геометричній сумі переміщення тіла відносно рухомої системи координат і переміщення власне рухомої системи координат відносно нерухомої. У […]...

  14. ВІДНОСНІСТЬ РУХУ. КЛАСИЧНИЙ ЗАКОН ДОДАВАННЯ ШВИДКОСТЕЙ Фізика підготовка до ЗНО комплексне видання МЕХАНІКА 1. ОСНОВИ КІНЕМАТИКИ 1.3. ВІДНОСНІСТЬ РУХУ. КЛАСИЧНИЙ ЗАКОН ДОДАВАННЯ ШВИДКОСТЕЙ Відносність механічного руху полягає в тому, що вид траєкторії, шлях і переміщення залежать від вибору системи відліку. Класичний закон додавання швидкостей: Швидкість тіла відносно системи, яку вважають нерухомою, дорівнює геометричній сумі швидкості тіла в рухомій системі відліку й […]...

  15. Неінерційні системи відліку ФІЗИКА Частина 1 МЕХАНІКА Розділ 2 ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ 2.8. Неінерційні системи відліку Дослід засвідчує, що закони Ньютона справджуються лише в інерційних системах відліку. Будь-яка неінерційна система рухається відносно інерційних систем із деяким прискоренням. У неінерційних системах відліку закони Ньютона не справджуються. Розглянемо це на прикладах. Нехай на гладенькій платформі без бортів (рис. 2.3) лежить […]...

  16. Висновки з перетворень Лоренца ФІЗИКА Частина 4 ОПТИКА. СПЕЦІАЛЬНА ТЕОРІЯ ВІДНОСНОСТІ Розділ 14 ШВИДКІСТЬ ПОШИРЕННЯ СВІТЛА. ОСНОВИ СПЕЦІАЛЬНОЇ ТЕОРІЇ ВІДНОСНОСТІ 14.6. Висновки з перетворень Лоренца Слід зазначити, що у формули перетворень Лоренца (14.9) і (14.10) входять не довжини відрізків і не проміжки часу, а координати окремих подій. Наприклад, час t відлічується за годинником, який перебуває в стані спокою в […]...

  17. Перший закон Ньютона – Динаміка 5. Механіка 5.2. Динаміка 5.2.6. Перший закон Ньютона Існують системи відліку, відносно яких тіла рухаються рівномірно і прямолінійно або ж перебувають в стані спокою, коли на них не діють інші тіла або дія інших тіл компенсується....

  18. Релятивістська динаміка Формули й таблиці ФІЗИКА ЕЛЕМЕНТИ ТЕОРІЇ ВІДНОСНОСТІ Відносність відстаней L – довжина предмета, що рухається, ; L0 – довжина нерухомого предмета, ; υ – швидкість руху предмета в даній інерційній системі відліку (ІСВ), ; С – швидкість світла у вакуумі, с = 2,998 · 108 м/c. Відносність проміжків часу τ0 – інтервал часу між двома […]...

  19. Тіло відліку. Система відліку. Матеріальна точка МЕХАНІКА РОЗДІЛ 2. МЕХАНІЧНИЙ РУХ § 15. Тіло відліку. Система відліку. Матеріальна точка Запитання до вивченого 1. Тіло, відносно якого розглядають рух, називають тілом відліку. 2. Щоб говорити про те, рухається тіло чи перебуває у стані спокою, потрібно спочатку вибрати тіло відліку, а потім пересвідчитися, чи змінюється відносно нього положення досліджуваного тіла. 3. Пасажир, який […]...

  20. ТІЛО ВІДЛІКУ. СИСТЕМА ВІДЛІКУ. МАТЕРІАЛЬНА ТОЧКА Роздiл 2 МЕХАНІЧНИЙ РУХ &15. ТІЛО ВІДЛІКУ. СИСТЕМА ВІДЛІКУ. МАТЕРІАЛЬНА ТОЧКА Щo6 визначити, рухається тіло чи ні, ми повинні вказати, відносно якого тіла розглядаємо рух. Тіло, відносно якого розглядають рух, називають тілом відліку. Тіла відліку обирають довільно. Під час вивчення різних рухів за тіло відліку прийматимемо Землю, пароплав, будинок, поїзд або будь-яке інше тіло, нерухоме […]...

  21. ПЕРШИЙ ЗАКОН НЬЮТОНА – ЗАКОН ІНЕРЦІЇ Фізика підготовка до ЗНО комплексне видання МЕХАНІКА 2. ОСНОВИ ДИНАМІКИ 2.1. ОСНОВНІ ЗАКОНИ ДИНАМІКИ. СИЛА. РІВНОДIЙНА СИЛА 2.1.1. ПЕРШИЙ ЗАКОН НЬЮТОНА – ЗАКОН ІНЕРЦІЇ Існують такі системи відліку, відносно яких поступально рухоме тіло зберігає свою швидкість сталою, якщо на нього не діють інші тіла (або вплив інших тіл компенсується). Такі системи відліку називаються інерціальними. Інерціальна […]...

  22. Відносність механічного руху. Закон додавання швидкостей КІНЕМАТИКА Урок № 4 Тема. Відносність механічного руху. Закон додавання швидкостей Мета: перевірити знання графіків руху і вміння їх будувати та читати; сформувати знання про відносність руху і спокою тіла, сформулювати правило додавання переміщень і швидкостей під час відносного руху, виробити вміння визначати швидкість і переміщення тіл відносно різних систем відліку, переконати учнів у життєвій […]...

  23. Фізика простору і часу. Принцип еквівалентності ФІЗИКА Частина 4 ОПТИКА. СПЕЦІАЛЬНА ТЕОРІЯ ВІДНОСНОСТІ Розділ 14 ШВИДКІСТЬ ПОШИРЕННЯ СВІТЛА. ОСНОВИ СПЕЦІАЛЬНОЇ ТЕОРІЇ ВІДНОСНОСТІ 14.11. Фізика простору і часу. Принцип еквівалентності Представники класичної фізики не наважувались науково дослідити й розкрити властивості простору й часу. Ці властивості вважали наперед заданими і визначали найпростішими аксіомами математики. І. Ньютон розглядав простір як абсолютний, істинний, математичний, а […]...

  24. Механічний рух. Відносність руху. Система відліку МЕХАНІКА РОЗДІЛ 2. МЕХАНІЧНИЙ РУХ § 7. Механічний рух. Відносність руху. Система відліку Контрольні запитання 1. Механічний рух – це зміна з часом положення тіла або частин тіла в просторі відносно інших тіл. Але треба пам’ятати, що в науці розрізняють три рівні будови всесвіту: мікросвіт, макросвіт і мегасвіт. До мікросвіту належать атоми, молекули, йони, а […]...

  25. ВІДНОСНІСТЬ ПРОМІЖКУ ЧАСУ – ВИСНОВКИ СТВ Фізика підготовка до ЗНО комплексне видання КВАНТОВА ФІЗИКА. ЕЛЕМЕНТИ ТЕОРІЇ ВІДНОСНОСТІ 1. ЕЛЕМЕНТИ ТЕОРІЇ ВІДНОСНОСТІ 1.3. ВИСНОВКИ СТВ 1.3.2. ВІДНОСНІСТЬ ПРОМІЖКУ ЧАСУ Час, виміряний у системі відліку, де точки системи нерухомі, називається власним часом (t0). Час у рухомій системі відліку: Якщо υ ” с, то t = t0 – класична механіка. Релятивістське уповільнення часу в […]...

  26. Релятивістський закон додавання швидкостей 2-й семестр МЕХАНІКА 5 . Релятивістська механіка Урок 2/69 Тема. Релятивістський закон додавання швидкостей Мета уроку: ознайомити учнів з релятивістським законом додавання швидкостей Тип уроку: вивчення нового матеріалу План уроку Демонстрації 5 хв. Фрагмент відеофільму “Принцип відносності Галілея” Вивчення нового матеріалу 30 хв. 1. Класичний закон додавання швидкостей. 2. Релятивістський закон додавання швидкостей. 3. Відносність […]...

  27. Інерційні системи відліку ФІЗИКА Частина 1 МЕХАНІКА Розділ 2 ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ 2.3. Інерційні системи відліку Тіло або сукупність тіл, які умовно вважаються нерухомими і відносно яких розглядається рух інших тіл, називають у фізиці тілами відліку. Систему відліку можна вибрати довільно. При цьому рух будь-якого тіла в різних системах відліку матиме неоднаковий вигляд, тобто тіло рухатиметься, наприклад, по […]...

  28. АНАЛІЗ КОНТРОЛЬНОЇ РОБОТИ № 1. МЕХАНІЧНИЙ РУХ. ВІДНОСНІСТЬ РУХУ. ТІЛО ВІДЛІКУ. СИСТЕМА ВІДЛІКУ. МАТЕРІАЛЬНА ТОЧКА. ТРАЄКТОРІЯ. ШЛЯХ. ПЕРЕМІЩЕННЯ Тип уроку: комбінований урок. Мета: увести поняття “механічний рух”, ознайомити учнів з основними поняттями, що характеризують механічний рух, ознайомити з видами механічного руху, надати уявлення про відносність механічного руху. Обладнання та наочність: дослід з відносності руху, спідометр. Відеофрагмент: види рухів, відносність руху. Хід уроку I. ОРГАНІЗАЦІЙНИЙ ЕТАП II. АНАЛІЗ ВИКОНАННЯ КОНТРОЛЬНОЇ РОБОТИ № 1 III. […]...

  29. Підсумковий урок з теми “Релятивістська механіка” РЕЛЯТИВІСТСЬКА МЕХАНІКА Урок № 4 Тема. Підсумковий урок з теми “Релятивістська механіка” Мета: узагальнити та поглибити знання учнів з вивченої теми; сформувати в учнів усвідомлення пізнаваності світу; встановити зв’язки мікро – і макросвіту на основі розгляду теорії відносності в астрономії й атомній фізиці; формувати в учнів уявлення про роль науки в житті суспільства, значення громадської […]...

  30. Тіло відліку – Кінематика 5. Механіка 5.1. Кінематика 5.1.4. Тіло відліку Тіло відліку – це тіло, відносно якого розглядається механічний рух фізичного тіла і де розміщується початок уявної системи координат, в якій розглядається рух тіла....

  31. Основні положення СТВ 2-й семестр МЕХАНІКА 5 . Релятивістська механіка – Принцип відносності Ейнштейна – Основні положення СТВ – Швидкість світла у вакуумі – Взаємозв’язок маси й енергії Тематичне планування № з/п Тема уроку Дата проведення 1 Основні положення СТВ 2 Релятивістський закон додавання швидкостей. Відносність одночасності подій 3 Основні наслідки, що випливають з постулатів теорії відносності 4 […]...

  32. Траєкторія – Кінематика 5. Механіка 5.1. Кінематика 5.1.3. Траєкторія Траєкторія – це уявна неперервна лінія, яку описує фізичне тіло під час механічного руху відносно обраної системи відліку. Вигляд траєкторії залежить від сил, що діють на тіло, початкових умов і системи відліку. Залежно від траєкторії рухи поділяються на прямолінійні і криволінійні. Прямолінійний рух – це рух фізичного тіла (матеріальної […]...

  33. ОСНОВНІ ПОНЯТТЯ – МЕХАНІКА ТВЕРДОГО ТІЛА Фізика підготовка до ЗНО комплексне видання МЕХАНІКА 2. ОСНОВИ ДИНАМІКИ 2.4. МЕХАНІКА ТВЕРДОГО ТІЛА 2.4.1. ОСНОВНІ ПОНЯТТЯ Найпростішими видами механічного руху твердого тіла є поступальні й обертальні рухи. Поступальний рух тіла може бути охарактеризований рухом однієї будь-якої його точки, наприклад центра мас. При обертальному русі твердого тіла його точки описують кола, розташовані в паралельних площинах. […]...

  34. Перший принцип термодинаміки ФІЗИКА Частина 2 МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА Розділ 7 ОСНОВИ ТЕРМОДИНАМІКИ 7.4. Перший принцип термодинаміки Перший принцип термодинаміки є узагальнювальним законом збереження і перетворення енергії, сформульованим щодо процесів, у яких бере участь теплота. Перший принцип термодинаміки можна сформулювати так: надана системі теплота витрачається на збільшення її внутрішньої енергії, а також на роботу проти зовнішніх сил. […]...

  35. Перший закон Ньютона ФІЗИКА Частина 1 МЕХАНІКА Розділ 2 ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ 2.2. Перший закон Ньютона Кінематика не розкриває причин руху. Вона лише описує сам рух. Розкрити причини руху не так просто. До Галілея протягом майже двох тисяч років існувала динаміка Арістотеля (384-322 до н. е.). За Арістотелем, небесні тіла за своєю природою відмінні від земних і рухаються […]...

  36. ОСНОВНІ ПОНЯТТЯ Фізика підготовка до ЗНО комплексне видання МЕХАНІКА 1. ОСНОВИ КІНЕМАТИКИ 1.1. ОСНОВНІ ПОНЯТТЯ Кінематика – це розділ механіки, що вивчає механічний рух тіл, не розглядаючи причин, які цей рух зумовлюють. Механічний рух – це зміна з часом положення тіла в просторі відносно інших тіл. У шкільному курсі кінематики розглядають рівномірний прямолінійний рух, рівноприскорений прямолінійний рух, […]...

  37. Третій принцип термодинаміки. Від’ємні температури ФІЗИКА Частина 2 МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА Розділ 7 ОСНОВИ ТЕРМОДИНАМІКИ 7.12. Третій принцип термодинаміки. Від’ємні температури У 1906 р. принципи термодинаміки було доповнено тепловою теоремою Нернста. Ця теорема не випливає з першого і другого принципів, а виражає новий закон природи, тому її часто називають третім принципом термодинаміки. Суть його полягає в тому, що при […]...

  38. Сила Коріоліса ФІЗИКА Частина 1 МЕХАНІКА Розділ 2 ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ 2.10. Сила Коріоліса Розглянемо прямолінійний рух із погляду спостерігача, який перебуває у лабораторії, що обертається. Теорію такого руху розробив 1835 р. французький учений Г. Коріоліс (1792-1843). Нехай тіло масою m рухається вздовж меридіана зі швидкістю υ’ відносно Землі (рис. 2.4). Рис. 2.4. Якби тіло перебувало в […]...

  39. Відносність механічного руху 1-й семестр МЕХАНІКА 1. Кінематика Урок 3/5 Тема. Відносність механічного руху Мета уроку: розширити й поглибити знання про відносність руху; сформувати навички додавання швидкостей і переміщень, переходу від однієї системи відліку до іншої Тип уроку: вивчення нового матеріалу План уроку Контроль знань 5 хв. 1. Прямолінійний рівномірний рух. 2. Переміщення в разі прямолінійного рівномірного руху. […]...

  40. Система відліку – Кінематика 5. Механіка 5.1. Кінематика 5.1.7. Система відліку Система відліку – це тіло відліку, пов’язана з ним система координат і засіб для вимірювання часу....

Ви зараз читаєте: Принцип відносності Галілея
«
»