Пряма пропорційність
Розв’яжіть задачі
946. 1) ні; 2) так; 3) ні; 4) ні.
947. 1) ні; 2) ні; 3) ні; 4) ні; 5) так.
948. малюнок 57.
949. 1) ні; 2) так; 3) ні.
950. 1) k = 4; 2) k = -0,7; 3) k = 2/3.
951. 1) ні; 2) так; 3) ні.
952. 1) ні; 2) так; 3) ні.
953. 1) гострий, k = 3 > 0; 2) тупий, k = -7 < 0; 3) тупий, k = -0,6 < 0.
954. 1) ні; 2) так, t’ – аргумент; 3) ні.
955. А(1; 1); В(2; 2); Е(-2; -2).
956. А(1; 2); D(-3; -6).
957. 1) при x = -1, у = -0,5; при x = 0, у = 0; при x = 1, у = 0,5; при x = 2, у = 1; 2) у = 0, x = 0; 3) x = 1; 1,5; 2; 4) x = -1; -1,5; -2.
958. 1) при х = -2, у = 1; при х = -1; у = 0,5; при х = 0, у = 0; при x = 1, у = -0,5; 2) у = 0, х = 0; 3) х = -1; -1,5; -2; 4) х = 1; 1,5; 2.
959. при х = -2, у = 3 • (-2) = -6;
960. 1) y = 1,5x;
2)
X | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
Y(х) | -4,5 | -3 | -1,5 | 0 | 1,5 | 3 | 4,5 | 6 | 7,5 | 9 |
3)
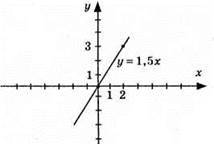
961. 1) у = -2,1х;
2)
X | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
Y(x) | 8,4 | 6,3 | 4,2 | 2,1 | 0 | -2,1 | -4,2 | -6,3 |
3)
962. 1) ні; 2) ні; 3) ні; 4) так.
963. 1) -2,5 ≠ 5/6 • 3; -2,5 ≠ 2,5; А не належить графіку;
2) 1 ≠ 5/6 • 6; 1 ≠ 5; В не належить графіку;
3) 5 = 5/6 • 6; 5 = 5; С належить графіку функції;
4) 10 = 5/6 • 12; 10 = 5 • 2; 10 = 10; D належить графіку функції.
964. 1) 1,3 = -1,3 • (-1); 1,3 = 1,3; K належить графіку;
2) 1,3 ≠ -1,3 • 1; 1,3 ≠ -1,3; L не належить графіку;
3) 3,9 ≠ -1,3 • 3; 3,9 ≠ -3,9; М не належить графіку;
4) 3,9 = -1,3 • (-3); 3,9 = 3,9; N належить графіку функції.
965. 1) -0,4 ≠ -0,4 • (-1); -0,4 ≠ 0,4; М не належить графіку;
2) -0,4 = -0,4 • 1; -0,4 = -0,4; N належить графіку;
3) 2 ≠ -0,4 • 5; 2 ≠ -2; Р не належить графіку функції;
4) 2 = -0,4 • (-5); 2 = 2; R належить графіку функції.
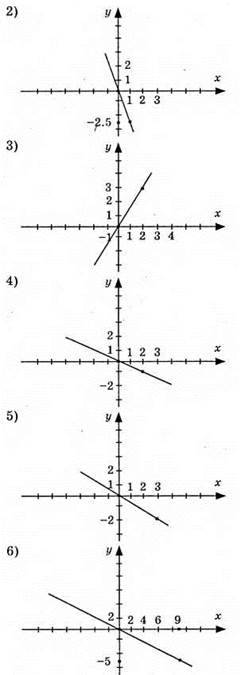
966. 1) (0; 0); (1; -1,2); (-2; 2,4); 2) (0; 0); (1; 3,5); (2; 7); 3) (0; 0); (1; -3/7); (-7; 3).
967. 1) у = х, графік – пряма, що проходить через початок координат; (0; 0); (1; 1);
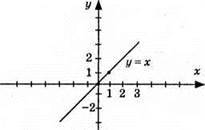
2) у = -3х, графік – пряма; (0; 0); (1; -3);
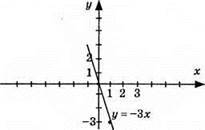
3) у = 0,25х, графік – пряма; (0; 0); (4; 1).
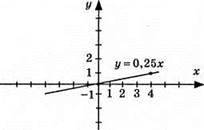
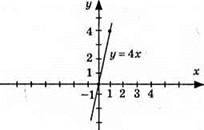
968. 1) у = 4х, графік – пряма, що проходить через початок координат (0; 0); (1; 4);
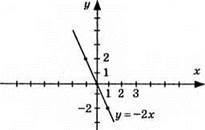
2) у = -2х, графік – пряма; (0; 0); (1; -2);
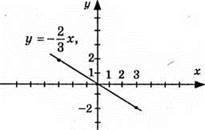
3) y = -2/3x, графік – пряма; (0; 0); (3; -2).
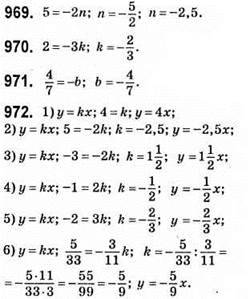
Графіки цих функцій:
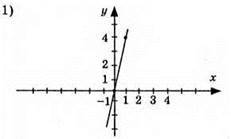
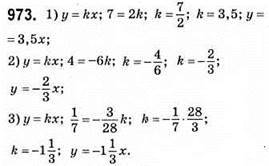
Графіки цих функцій:
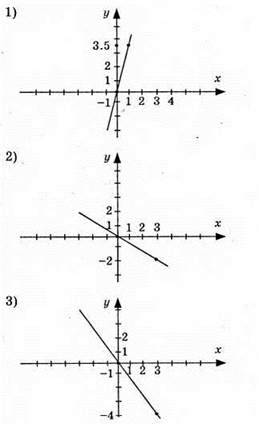
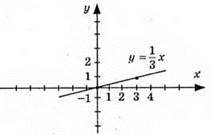
974. y = 1/3х – пряма пропорційність; (0; 0); (3; 1).
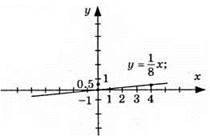
975. у = 1/8х; (0; 0); (4; 0,5).
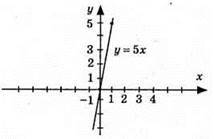
976. 
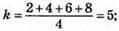y = 5х; (0; 0); (1; 5).
977.
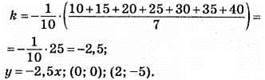
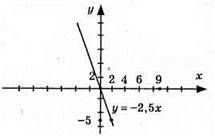
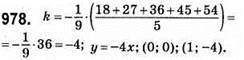
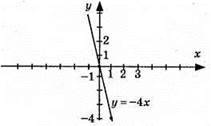
Графіки цих функцій є прямі, що проходять через початок координат.
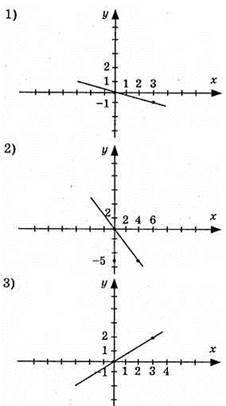
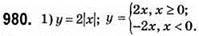
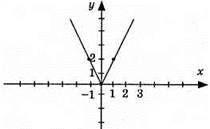
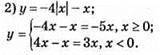
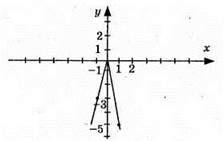
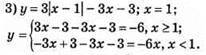
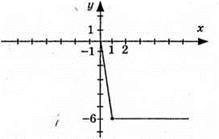
981. 1) у = 2х; 2) у = -2x; 3) y = 4x. Графіки цих функцій – прямі, що проходять через початок координат.
1) (0; 0); (1; 2);
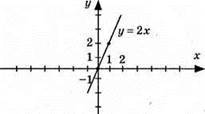
2) (0; 0); (1; -2);
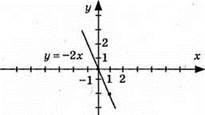
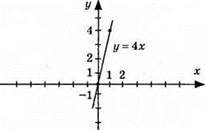
3) (0; 0); (1; 4).
Застосуйте на практиці.
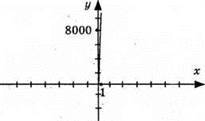
982. у = 8000x; х – кількість робочих днів; у – загальна кількість отриманих грошей, у = 8000 • 28 = 224 000 грн було отримано за місяць.
983. y = 2х; х – площа стіни; у – маса клею; 2,5 м • 3 м = 7,5 м2 – площа 1-ї стіни; 3 • 7,5 = 22,5м2 – площа 3-х стін; у = 2 • 22,5 = 45 кг – клею потрібно.
Задачі на повторення.
984. 450 м + 45 м + 4,5 м + 0,45 м = 499,95;
499,95 : 3 = 166,65 ≈ 167 стрибків потрібно зробити кенгуру.
985. Нехай друге число – х, тоді перше – 3,5x, а третє – 3,5x – 2,8:
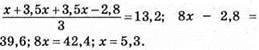
Числа 5,3; 18,55 і 15,75.
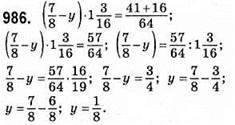
987. Число 9765.
(1 votes, average: 5.00 out of 5)
Loading...