Головна ⇒ 📌Математика ⇒ ПРЯМОКУТНИЙ ТРИКУТНИК

ПРЯМОКУТНИЙ ТРИКУТНИК

РОЗДІЛ 3 ТРИКУТНИКИ

& 16. ПРЯМОКУТНИЙ ТРИКУТНИК

Трикутник наливають прямокутним, якщо один із його кутів – прямий. Сума двох інших його кутів дорівнює 90°, бо 180° – 90° = 90°.

Сторона прямокутного трикутника, що лежить проти прямого кута, – це гіпотенуза, дві інші його сторони – катети (мал. 196). На малюнку прямий кут іноді позначають квадратиком. У кожному прямокутному трикутнику гіпотенуза більша від кожного катета.

Згодом нам будуть потрібні ознаки рівності прямокутних трикутників. З першої і другої ознак рівності

трикутників (див. & 12) безпосередньо випливають такі ознаки.

ПРЯМОКУТНИЙ ТРИКУТНИК

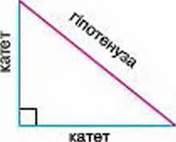
Мал. 196

Два прямокутні трикутники рівні, якщо:

1) катети одного з них дорівнюють відповідно катетам іншого:

2) катет і прилеглий гострий кут одного трикутника дорівнюють відповідно катету і прилеглому гострому куту іншого;

3) гіпотенуза і прилеглий кут одного трикутника дорівнюють відповідно гіпотенузі і прилеглому куту іншого.

Ще одна ознака рівності прямокутних трикутників потребує доведення.

Теорема 21 Якщо катет і гіпотенуза одного прямокутного трикутника дорівнюють відповідно катету і гіпотенузі

іншого, то такі трикутники – рівні.

Доведення. Нехай у трикутниках ABC і А1В1С1 кути С і С1 – прямі і АВ = А1В1, АС = А1С1 (мал. 197). Доведемо, що ∆АВС = ∆А1С1.

Прикладемо ∆A1B1C1 до трикутника АВС так, щоб вершина А1 сумістилась із вершиною А, С1 – із С, a ∆A1B1C1 зайняв положення трикутника AB2C. Оскільки кути С і С1 прямі, то точки В, С і В, розмістяться на одній прямій. ∆АВВ2 – рівнобедрений, ∠B = ∠B2 = ∠B1. Тоді ∠ВСА = ∠B2AC = ∠A1. Отже, у даних трикутниках між відповідно рівними сторонами АВ =А1В1, АС = A1С1 лежать рівні кути А і А1. За першою ознакою рівності трикутників ∆АВС = ∆А1В1С1.

ПРЯМОКУТНИЙ ТРИКУТНИК

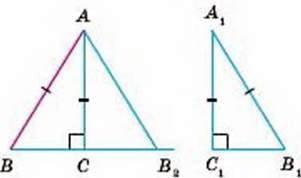
Мал. 197

ПРЯМОКУТНИЙ ТРИКУТНИК

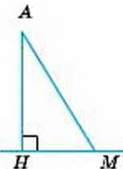
Мал. 198

Уведемо ще кілька важливих понять, пов’язаних з прямокутним трикутником. Якщо АНМ – прямокутний трикутник із прямим кутом Н, то його катет AН – перпендикуляр, проведении я точки А на пряму НМ (мал. 198).

Гіпотенузу AM називають також похилою, проведеною з точки А до прямої НМ, а катет НМ – проекцією цієї похилої на пряму НМ.

Довжину перпендикуляра АН називають також відстанню від точки А до прямої НМ.

Узагалі, відстань між двома геометричними фігурами – це відстань між їх найближчими точками (якщо такі точки існують). Наприклад, відстань між двома паралельними прямими дорівнює довжині перпендикуляра, проведеного з будь-якої точки однієї прямої на іншу (мал. 199). А відстань від точки К до відрізка РТ, зображених на малюнку 200, дорівнює КТ.

Розглянемо деякі властивості прямокутних трикутників.

ПРЯМОКУТНИЙ ТРИКУТНИК

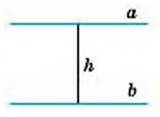
Мал. 199

ПРЯМОКУТНИЙ ТРИКУТНИК

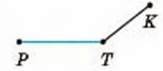
Мал. 200

Теорема 22 У прямокутному трикутнику гіпотенуза більша за катет.

Доведення. У кожному трикутнику проти більшого кута лежить більша сторона (ДИВ. теорема 19). Оскільки гіпотенуза лежить проти прямого кута, а катет – проти гострого, і прямий кут більший за гострий, то гіпотенуза – більша за катет.

Наслідок Якщо з однієї точки, яка не лежить на прямій, до цієї прямої проведено перпендикуляр і похилу, то:

1) перпендикуляр менший від похилої;

2) проекція похилої менша від похилої.

Ще одни дуже цікава властивість прямокутних трикутників наведена в рубриці “Виконаємо разом”.

Для допитливих

Прямокутні трикутники становлять тільки частину всіх трикутників. Якщо трикутник не має прямого куга, його називають непрямокутним трикутником. Отже, залежно від того, має чи не має трикутник прямий кут, усі трикутники можна поділити на два класи. Схематично цей поділ можна зобразити малюнком 201.

Якщо катети прямокутного трикутника рівні, то він водночас є і рівнобедреним трикутником. Співвідношення між такими видам и три кутників можна зобразити, як показано на малюнку 202.

ПРЯМОКУТНИЙ ТРИКУТНИК

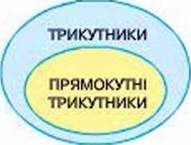
Мал. 201

ПРЯМОКУТНИЙ ТРИКУТНИК

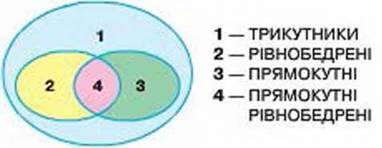
Мал. 202

Прямокутні трикутники в геометрії відіграють важливу роль, бо будь-який трикутник можна розрізати на два прямокутні трикутники, а для кожного прямокутного трикутника справджується славнозвісна теорема Піфагора: квадрат гіпотенузи дорівнює сумі квадратів катетів. Докладніше про теорему Піфагора і про застосування властивостей прямокутних трикутників ви дізнаєтесь у 8 класі.

Запитання і завдання для самоконтролю

1. Сформулюйте означення прямокутного трикутника.

2. Як називають сторони прямокутного трикутника?

3. Сформулюйте і доведіть ознаки рівності прямокутних трикутників.

4. Що таке перпендикуляр, похила і проекція похилої?

5. Що таке відстань від точки до прямої?

6. Що таке відстань між фігурами?

7. Сформулюйте та доведіть властивості прямокутних трикутників.

Виконаємо разом

Катет прямокутного трикутника, яким лежить проти кута 30°, дорівнює половині гіпотенузи. Доведіть.

– Нехай у ∆АВС ∠C = 90° і ∠A = 30° (Maл. 203). Доведемо, що ВС = 0,5 АВ.

ПРЯМОКУТНИЙ ТРИКУТНИК

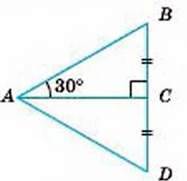
Мал. 203

На прямій DC відкладемо відрізок CD, рівний стороні СВ, і проведемо відрізок AD. За двома катетами ∆ВСА = ∆DCA. Оскільки ∠BAD = 60°, то ∠B = ∠D = (180° – 60°) : 2 = 60°. Отже, всі кути трикутника ABD дорівнюють по 60°. Таку властивість мас тільки рівносторонній трикутник. Оскільки ВD = AВ і ВC = CD, то ВС = 0,5 AВ.

ЗАДАЧІ І ВПРАВИ

Виконайте усно

465. Знайдіть кути прямокутного трикутника, якщо один із них дорівнює: а) 30°; б) 46°; в) 70°.

466. Знайдіть гострі кути прямокутного трикутника, якщо один із них більший за інший: а) удвічі; б) у 9 разів; в) на 30°.

467. Сторони прямокутного трикутника дорівнюють 3 м, 4 м і 5 м. Яка з них – гіпотенуза?

468. Знайдіть кути рівнобедреного прямокутного трикутника.

А

469. Один із гострих кутів прямокутного трикутника на 10° більший за інший. Знайдіть ці кути.

470. Кути трикутника пропорційні числам 3, 5 і 8. Доведіть, що цей трикутник прямокутний.

471. Один із кутів трикутника на 30° більший за другий і на 30° менший від третього. Знайдіть кути цього трикутника.

472. Доведіть, що бісектриси гострих кутів прямокутного трикутника перетинаються під кутом 46°.

473. Знайдіть кути прямокутного трикутника, якщо його висота, проведена з вершини прямого кута, утворює: з катетом кут 50°.

474. Із точки D, яка лежить на бісектрисі кута В, на сторони кута проведено перпендикуляри DA і DC. Доведіть, що DA = DC.

475. Точка В лежить на внутрішньому промені кута A; DK і DM – рівні перпендикуляри до сторін кута. Доведіть, що АВ – бісектриса кута А.

476. Пряма m перетинає відрізок АВ в його середині О. Доведіть, що точки А і В рівновіддалені від прямої m.

477. Якщо катет і протилежний кут одного трикутника дорівнюють відповідно катету і протилежному куту іншого, то такі трикутники – рівні. Доведіть.

478. У ∆АВС ∠С = 90°, ∠А = 60°, AD = 32 см. Знайдіть АС.

479. За малюнком 204 поясніть, як можна знайти ширину річки на основі властивостей прямокутного рівнобедреного трикутника.

480. Прямокутні трикутники ABC і А1В1С розташовані, як показано на малюнку 205. Знайдіть міру кута АСА1, якщо ∠BCB1 = а (грецька літера “альфа”).

ПРЯМОКУТНИЙ ТРИКУТНИК

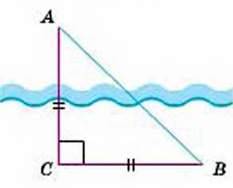
Мал. 204.

ПРЯМОКУТНИЙ ТРИКУТНИК

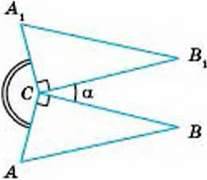
Мал. 205

Б

481. Сформулюйте і доведіть твердження, обернене до сформульованого в задачі, розв’язанні на с. 114.

482. У трикутнику ABC АВ = 18 см. ∠B = 30°, ∠C = 90°. Знайдіть:

А) відстань від точки А до прямої СВ;

Б) проекцію похилої АВ на пряму АС.

483. У трикутнику ABC ∠A = ∠B = 46°, АВ = 19 см. Знайдіть:

А) відстань від точки С до прямої АВ;

Б) проекцію відрізка АС на пряму АВ.

484. Знайдіть відстань між паралельними прямими, якщо від січної, яка перетинає їх під кутом 30°, прямі відтинають відрізок завдовжки 54 см.

485. Знайдіть кути прямокутного трикутника, якщо бісектриси двох його кутів перетинаються під кутом 70°.

486. Чи можуть бісектриси двох кутів прямокутного трикутника перетинатися під кутом 40°?

487. Знаючи, що всі сторони квадрата рівні, а всі кути прямі, доведіть, що квадрат ABCD відрізками АС і BD розбивається на 4 рівні прямокутні рівнобедрені трикутники.

488. Побудуйте на координатній площині трикутники з вершинами А (0; 1), В (2; 3), С (0; 3) і з вершинами К (1; 0), Р (3; 0), Т (3; 1). Чи рівні ці трикутники?

489. Медіана якого трикутника розбиває його на два менші трикутники, рівні між собою? Укажіть вид утворених трикутників.

490. CM – висота прямокутного рівнобедреного трикутника ABC, проведена до гіпотенузи. Знайдіть АВ, якщо CM = m.

491. Гіпотенуза АВ прямокутного трикутника ABC дорівнює 20 см, ∠B = 30°, СК – висота. Знайдіть АК.

Практичне завдання

492. Розгляньте малюнок 206. У такий спосіб давньогрецький учений Фалес Мілетський запропонував вимірювати відстань КС до корабля, який знаходився в морі.

Робилося це так. Нехай у точці К знаходиться корабель, а в точці С – спостерігач. Від пункту спостереження С намічали напрямок на корабель К і до цього напрямку на березі з точки С відкладали перпендикулярний напрямок, на якому будували довільний відрізок СВ і знаходили його середину О. У точці В намічався напрямок, перпендикулярний до напрямку СВ в сторону суші. Спостерігач ішов у напрямку ВА, дивлячись на корабель. Як тільки корабель і пункт О опинялися на одній прямій, спостерігач фіксував точку А, і тоді відстань КС дорівнювала відстані АВ, яку можна було знайти безпосереднім вимірюванням.

Спробуйте й ви визначити відстань до недоступного об’єкта таким способом.

ПРЯМОКУТНИЙ ТРИКУТНИК

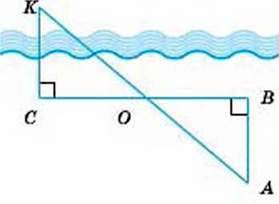
Мал. 206

ВПРАВИ ДЛЯ ПОВТОРЕННЯ

493. ∆АВС = ∆MNK, ∠A = 70°, ∠B = 80°. Знайдіть кути трикутника МNK.

494. Чи існує трикутник, кути якого дорівнюють 91°, 52° і 44°?

495. Рівні відрізки АВ і CD перетинаються в точці О так, що АО = СО, а кути трикутника AOD – пропорційні числам 2, 3 і 5. Знайдіть кути трикутника СОВ.

496. Перемалюйте в зошит фігуру, що на малюнку 207, і проведіть пряму так, щоб вона розрізала зафарбовану фігуру на дві частини рівних площ.

ПРЯМОКУТНИЙ ТРИКУТНИК

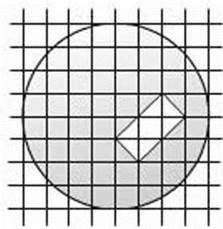
Мал. 207

ЗАДАЧІ ЗА ГОТОВИМИ МАЛЮНКАМИ

А

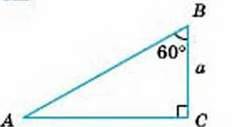
1

ВС = а.

АВ

ПРЯМОКУТНИЙ ТРИКУТНИК

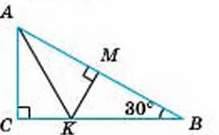
2

АК = КВ = 8.

СВ, КМ

ПРЯМОКУТНИЙ ТРИКУТНИК

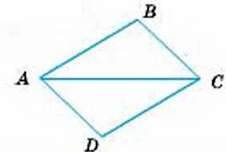
3

АВ = CD, AD = ВС.

Довести:

AD | ВС.

ПРЯМОКУТНИЙ ТРИКУТНИК

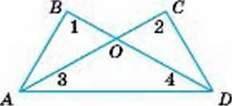
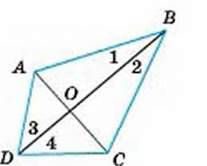
4

∠1 = ∠2, ∠3 = ∠4.

Довести: ∆АBО = ∆DCО.

ПРЯМОКУТНИЙ ТРИКУТНИК

Б

1

∠1 = ∠2, ВК = 10.

АК, КC

ПРЯМОКУТНИЙ ТРИКУТНИК

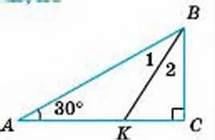
2

АВ = CD, АС = BD.

∠AOD

ПРЯМОКУТНИЙ ТРИКУТНИК

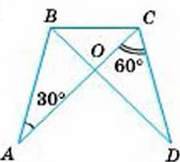
3

∠1 = ∠2, BM = MC.

Довести:

AM ⏊ ВС.

ПРЯМОКУТНИЙ ТРИКУТНИК

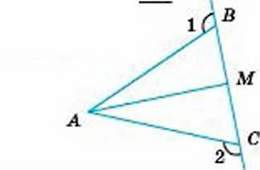
4

∠1 = ∠2, ∠3 = ∠4.

Довести: АС ⏊ BD.

ПРЯМОКУТНИЙ ТРИКУТНИК

Самостійна робота 4

Варіант 1

1. Сформулюйте означення рівнобедреного трикутника.

2. ∆ABC – прямокутний (АС = 90°). Знайдіть ∠A, якщо ∠В = 70°.

З. Точки К і Р – середини бічних сторін АВ і АС рівнобедреного трикутники ABC. Доведіть, що ∆АКС = ∆АРВ.

4. Знайдіть кути трикутника, якщо один із них удвічі більший за другий і на 40° менший від третього.

Варіант 2

1. Сформулюйте означення прямокутного трикутника.

2. ∆АВС – рівнобедрений (АВ = ВС). Знайдіть ∠A, якщо ∠В = 70°.

З. Точки К і Р – середини бічних сторін АВ і АС рівнобедреного трикутники ABC. Доведіть, що ∆КВС = ∆РСВ.

4. Знайдіть кути трикутника, якщо один із них удвічі менший від другого і на 12° більший за третій.

Варіант З

1. Сформулюйте властивість кутів рівнобедреного трикутника.

2. ∆АВС – прямокутний (АС = 90°) і рівнобедрений. Знайдіть АВ.

З. Точки К і М лежать на основі АС рівнобедреного трикутника ABC, ∠ВКА = ∠ВМС. Доведіть, що ВК = ВМ.

4. Знайдіть кути трикутника, якщо один із них утричі більший за другий і на 40° менший від третього.

Варіант 4

1. Сформулюйте одну з ознак рівності прямокутних трикутників.

2. ∆АВС – рівнобедрений (АВ = ВС). Знайдіть ∠B, якщо АС = 60°.

3. Точки К і М лежать на основі АС рівнобедреного трикутника ABC, ∠ВКА = ∠ВМС. Доведіть, що AК = CM.

4. Знайдіть кути трикутника, якщо один із них утричі менший від другого і на 5° більший за третій.

Тестові завдання 4

1. 1. Периметр рівнобедреного трикутника з основою 6 см і бічною стороною 5 см дорівнює:

А) 17 см; б) 16 см;

В) 11 см; г) 30см.

2. 2. Один із кутів рівнобедреного трикутника дорівнює 100″. Обчисліть інші кути трикутника.

A) 100° і 60°; б) 80° і 80°;

В) 40° і 40°; г) 100° і 160°.

3. 3. Кут при вершині В рівнобедреного трикутника ABC (АВ = ВС) дорівнює 80°. Обчисліть кут між бічною стороною і медіаною, проведеною з вершини В.

А) 60°; б) 40°;

В) 60°; г) 25°.

4. 4. Кут при основі рівнобедреного прямокутного трикутника дорівнює:

А) 45°; б) 60°;

В) 30°; г) 90°.

5. 5. Гіпотенуза прямокутного трикутника дорівнює 20 см, один із його кутів – 30°. Довжина меншого катета дорівнює:

А) 20 см; б) 5 см;

В) 10 см; г)15см.

6. 6. Кути трикутника пропорційні числам 4, 5 і 9. Даний трикутник:

А) гострокутний;

Б) прямокутний;

В) тупокутний;

Г) рівнобедрений.

7. 7. Діагональ АС прямокутника ABCD розбиває його на два трикутники. Яке з тверджень – хибне?

А) ∆АВС = ∆CDA;

Б) ∠ВАС = ∠ACD;

В) ∠АСВ = ∠ACD;

Г) ∠ABC = ∠ADC.

8. 8. Один із катетів прямокутного трикутника дорівнює 5 см, а прилеглий кут – 60°. Гіпотенуза трикутника дорівнює:

А) 10 cм; б) 5 cм;

В) 2,5см; г) 20см.

9. 9. У трикутник у АВС ∠A = 50°, ∠B = 70°. Який знак слід поставити замість * в записі: АВ * ВС?

А)<; б) =;

В)<; г)>.

10. Один із кутів прямокутного трикутника дорівнює 60°, а сума найменшої і найбільшої його сторін – 6 см. Знайдіть довжину гіпотенузи.

А) 7 см; б) 2 см;

В) 4 см; г) 1 см.

ТИПОВІ ЗАДАЧІ ДЛЯ КОНТРОЛЬНОЇ РОБОТИ

1. Периметр рівнобедреного трикутника дорівнює 112 см, а основа – 34 см. Знайдіть бічну сторону.

2. Знайдіть:

А) кути рівнобедреного прямокутного трикутника;

Б) зовнішні кути цього трикутника.

3. Знайдіть кути рівнобедреного трикутника, якщо його бічна сторона дорівнює 17 см, а периметр – 51 см.

4. Трикутники ABC і КРН рівносторонні й АВ = КР. Знайдіть:

А) КН, якщо ВС = 5 см;

Б) периметри ∆АВС і ∆КРН.

5. Знайдіть кути рівнобедреного трикутника, якщо його кут при вершині втричі більший за кут при основі.

6. Периметр рівнобедреного трикутника дорівнює 73 см. Знайдіть сторони цього трикутника, якщо його бічна сторона на 7 см менша від основи.

7. Кути трикутника ABC пропорційні числам 1, 2 і 3. Знайдіть:

А) кути ∆АВС;

Б) встановіть вид ∆АВС;

В) знайдіть найбільшу сторону ∆АВС, якщо найменша його сторона дорівнює 4 см.

8. Доведіть, що два прямокутні трикутники рівні, якщо катет і протилежний кут одного відповідно дорівнюють катету і протилежному куту іншого.

9. Знайдіть за малюнком 208 міру кута СОВ, якщо АВ = CD, BD = АС, ∠BDA = 35°.

10. ВМ і B1М1 відповідно медіани трикутників ABC і А1В1С1. АВ = A1B1, АС =А1C1, ВМ = В1М1. Доведіть, що ∆АВС = ∆А1В1С1.

ПРЯМОКУТНИЙ ТРИКУТНИК

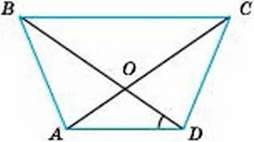
Мал. 208

Запитання і завдання для самоконтролю

1. Який трикутник називають рівнобедреним?

2. Як називають сторони рівнобедреного трикутника?

3. Сформулюйте властивість рівнобедреного трикутника про кути при основі.

4. Сформулюйте властивість бісектриси рівнобедреного трикутника.

5. Сформулюйте ознаки рівнобедреного трикутника.

6. Який трикутник називають різностороннім?

7. Який трикутник називають рівностороннім?

8. Як співвідносяться поняття трикутники і рівнобедрені трикутники?

9. Сформулюйте третю ознаку рівності трикутників.

10. Доведіть третю ознаку рівності трикутників.

11. Сформулюйте першу і другу ознаки рівності трикутників.

12. Як ви розумієте вислів: “трикутник визначається трьома його сторонами”?

13. Якими елементами визначається трикутник?

14. Як слід розуміти, що трикутник – фігура жорстка?

15. Сформулюйте означення прямокутного трикутника.

16. Як називають сторони прямокутного трикутника?

17. Сформулюйте і доведіть ознаки рівності прямокутних трикутників.

18. Сформулюйте і доведіть властивості прямокутних трикутників.

19. Сформулюйте властивість катета прямокутного трикутника, що лежить проти кута в 30°.

20. Що таке перпендикуляр, похила і проекція похилої?

21. Що таке відстань від точки до прямої?

22. Що таке відстань між фігурами?

23. Сформулюйте і доведіть теорему про залежність між сторонами і кутами трикутника.

24. Сформулюйте і доведіть теорему про нерівність трикутника.

25. Сформулюйте нерівності трикутника XYZ.

26. Що означає вислів: “точка В лежить між точками А і С”?

27. Як пов’язані між собою відстані між точками А, В і С, якщо точка В лежить між точками А і С?

28. Сформулюйте властивості відстаней між довільними точками А, В і С.

ГОЛОВНЕ В РОЗДІЛІ З

Трикутник – замкнена ламана із трьох ланок, або частіша площини, обмежена такою ламаною. Кожний трикутник має три сторони, три вершини і три кути. Сума довжин сторін трикутника – його периметр.

Сума кутів трикутника дорівнює 180°.

Важливу роль у геометрії відіграють ознаки рівності трикутників. Дві фігури називаються рівними, якщо їх можна сумістити. Якщо ∆АВС = ∆КРТ, то АВ = КР, ВС = РТ, СА = ТК, ∠А = ∠К, ∠В = ∠Р, ∠С = ∠Т.

Три ознаки рівності трикутників

Два трикутники рівні, якщо:

– дві сторони і кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними іншого трикутника (І);

– якщо сторона і прилеглі до неї кути одного трикутника дорівнюють відповідно стороні і прилеглим до неї кутам іншого (ІІ);

– якщо три сторони одного трикутника дорівнюють відповідно трьом сторонам іншого (III).

Трикутник називають рівнобедреним, якщо він мас дві рівні сторони. Рівні сторони рівнобедреного трикутника називають бічними сторонами, а третю – його основою.

У рівнобедреному трикутнику кути при основі – рівні, а бісектриса, проведена до основи, є медіаною і висотою.

Якщо трикутник має два рівні кути, то він – рівнобедрений.

Якщо всі сторони трикутника рівні, його називають рівностороннім трикутником. КОЖНИЙ кут рівностороннього трикутника дорівнює 60°.

Залежно від кутів трикутники поділяють на гострокутні, прямокутні й тупокутні.

Сторону прямокутного трикутника, яка лежить проти прямого кута, називають гіпотенузою, а дві інші – катетами.

Катет прямокутного трикутника, ЯКИЙ лежить проти кута 30°, дорівнює половині гіпотенузи.

Кожна сторона трикутника менша за суму двох інших його сторін і більша за їх різницю. Які б не були три точки площини А, В і С, завжди АВ + ВС ≥ АС.

У кожному трикутнику проти більшої сторони лежить більший кут, а проти більшого кута – більша сторона.


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Прямокутний трикутник Урок № 36 Тема. Прямокутний трикутник Мета: домогтися засвоєння учнями властивості прямокутного трикутника з гострим кутом 30° та оберненого твердження і схеми їх доведень; сформувати в учнів уміння відтворювати формулювання цих тверджень та використовувати їх для розв’язування задач; удосконалювати вміння використовувати набуті раніше знання для розв’язування задач на прямокутний трикутник. Тип уроку: засвоєння знань, умінь […]...

  2. Прямокутний трикутник Геометрія Основні властивості найпростіших геометричних фігур Прямокутний трикутник Трикутник називається Прямокутним, якщо він має прямий кут. Сторона, яка лежить проти прямого кута, називається Гіпотенузою. Сторони, що утворюють прямий кут, називаються Катетами. На рисунку – прямокутний. AB і BC – катети, AC – гіпотенуза. Теорема. Сума гострих кутів прямокутного трикутника дорівнює . Ознаки рівності прямокутних трикутників […]...

  3. РІВНОБЕДРЕНИЙ ТРИКУТНИК РОЗДІЛ 3 ТРИКУТНИКИ & 13. РІВНОБЕДРЕНИЙ ТРИКУТНИК Трикутник називають рівнобедреним, якщо в нього дві сторони рівні. Рівні сторони рівнобедреного трикутника навивають бічними сторонами, а третю його сторону – основою. Трикутник, який не є рівнобедреним, називають різностороннім. Трикутник, у якого всі сторони рівні, називають рівностороннім. Рівносторонній трикутник є окремим видом рівнобедреного трикутника (мал. 166). Рівнобедрений трикутник […]...

  4. Трикутник і його види Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 2. ДОДАВАННЯ І ВІДНІМАННЯ НАТУРАЛЬНИХ ЧИСЕЛ 14. Трикутник і його види З усіх многокутників трикутники мають найменшу кількість сторін. Трикутники можна розрізняти за видом їх кутів. Якщо всі кути трикутника гострі, то його називають гострокутним трикутником (рис. 117). Якщо один із кутів трикутника прямий, то його […]...

  5. ТРИКУТНИК І ЙОГО ЕЛЕМЕНТИ Основна ідея, якою пройнята вся математика, – це ідея рівності. Г. Спенсер РОЗДІЛ 3 ТРИКУТНИКИ У цьому розділі ви повторите свої знання про трикутники, здобуті в попередніх класах, і дізнаєтеся про багато інших їх властивостей. Основне в розділі – три ознаки рівності трикутників Вони часто використовуються в геометрії. Тому від того, як добре ви вивчите […]...

  6. Рівнобедрений трикутник Урок № 23 Тема. Рівнобедрений трикутник Мета: домогтися свідомого розуміння учнями понять: – умова та висновок теореми; – пряма та обернена теореми; – формулювання та доведення ознаки рівнобедреного трикутника. Сформувати вміння: – відтворювати теорему – ознаку рівнобедреного трикутника; – виділяти у формулюванні теореми умову та висновки; – використовуючи знання про пряму та обернену теореми, складати […]...

  7. Рівнобедрений трикутник і його властивості § 2. Трикутники 8. Рівнобедрений трикутник і його властивості Практичні завдання 196. 197. 198. Вправи 199. 1) Р = 13 + 2 х 8 = 29(см). Відповідь: 29 см. 2) Нехай х см – бічна сторона, тоді 15 + 2х = 39, тоді 2х = 39 – 15; 2х = 24; х = 24 : […]...

  8. ТРИКУТНИК ТА ЙОГО ВИДИ РОЗДІЛ 2 ДІЇ ПЕРШОГО СТУПЕНЯ З НАТУРАЛЬНИМИ ЧИСЛАМИ § 10. ТРИКУТНИК ТА ЙОГО ВИДИ Ви знаєте, що трикутник – це окремий вид многокутника. У нього 3 вершини, 3 сторони і 3 кути. Трикутник ABC на малюнку 119 має вершини А, В і С, сторони АВ, ВС i АС, кути ВАС, ABC і АСВ. Серед трикутників […]...

  9. Рівняння. Кути. Прямокутник. Трикутник і його види УРОК 41 Тема. Рівняння. Кути. Прямокутник. Трикутник і його види Мета: підготовити учнів до тематичної контрольної роботи. Тип уроку: повторення і систематизація знань. Хід уроку I. Актуалізація опорних знань Усні вправи 1. Знайти корінь рівняння: 1) х + 15 = 29; 2) 30 – х = 17; 3) х – 12 = 19; 4) 12 […]...

  10. Многокутник та його периметр. Трикутник. Види трикутників Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 21. Многокутник та його периметр. Трикутник. Види трикутників Якщо кінець ламаної збігається з її початком, то таку ламану називають замкненою. На малюнку 137 зображено замкнену ламану, що складається з п’яти ланок, причому ланки ламаної не перетинаються. Таку ламану називають многокутником. Зауважимо, що […]...

  11. КОЛО І ТРИКУТНИК РОЗДІЛ 4 КОЛО І КРУГ. ГЕОМЕТРИЧНІ ПОБУДОВИ & 20. КОЛО І ТРИКУТНИК Коло і трикутник можуть не мати спільних точок або мати 1, 2, 3, 4, 5, 6 спільних точок (відповідні малюнки виконайте самостійно). Заслуговують на увагу випадки, коли коло проходить через усі три вершини трикутника або коли воно дотикається до всіх сторін трикутника. Розглянемо […]...

  12. Трикутник – Геометричні фігури й величини Математика – Алгебра Геометричні фігури й величини Трикутник На рисунку зображений трикутник зі сто­ронами a, b і c. – формула периметра трикутника. Сума всіх кутів довіль­ного трикутника до­рів­нює . Кожний трикутник має принаймні два ­гострих кути. Види трикутників Види трикутників залежно від величини кутів (див. рисунок): а – гострокутний (усі кути гострі); б – тупокутний […]...

  13. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...

  14. Трикутник та його елементи Урок № 15 Тема. Трикутник та його елементи Мета: домогтися засвоєння учнями змісту понять: “трикутник”; “сторона, вершина, кут (внутрішній) трикутника”; “кут, протилежний стороні”; “кут, прилеглий до сторони”; “периметр трикутника”; “внутрішня та зовнішня область трикутника”. Сформувати вміння: – розпізнавати та називати елементи трикутників, зображених на рисунку; – за рисунком та символічним позначенням трикутника називати кути, протилежні […]...

  15. Трикутник і його види Урок 40 Тема. Трикутник і його види Мета: подальше закріплення знань учнями класифікації трикутників, доповнення їх алгоритмами побудови трикутників за двома сторонами і кутом між ними та за стороною і прилеглими кутами; формування вмінь розв’язування задач на побудову і вдосконалення вмінь розв’язувати задачі на обчислення периметрів прямокутника, квадрата і трикутника. Тип уроку: застосування знань, умінь, […]...

  16. Трикутник і його елементи Розділ 1. Найпростіші геометричні фігури та їх властивості § 9. Трикутник і його елементи 292. На мал. 194 зображені трикутники ABD, ABC, ОВС. Проти кута C в трикутнику АВС лежить сторона АB, в трикутнику DBC – сторона BD. Прилеглими до кута С в трикутнику ABC є сторони АС і ВС, в трикутнику DBC – сторони […]...

  17. ТРЕТЯ ОЗНАКА РІВНОСТІ ТРИКУТНИКІВ РОЗДІЛ 3 ТРИКУТНИКИ & 14. ТРЕТЯ ОЗНАКА РІВНОСТІ ТРИКУТНИКІВ Вам уже відомі дві ознаки рівності трикутників. Знаючи властивості рівнобедреного трикутника, можна довести ще одну ознаку. Теорема 18 (третя ознака рівності трикутників). Якщо три сторони одного трикутника дорівнюють відповідно трьом сторонам іншого трикутника, то такі трикутники – рівні. Доведення. Нехай у трикутниках ABC і А1В1С1 АВ […]...

  18. Прямокутний трикутник – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Прямокутний трикутник Теорема Піфагора:...

  19. СУМА КУТІВ ТРИКУТНИКА РОЗДІЛ 3 ТРИКУТНИКИ & 10. СУМА КУТІВ ТРИКУТНИКА Теорема 8 Сума кутів трикутника дорівняй: 180°. Доведення. Нехай ABC – довільний трикутник (мал. 130). Через йот вершину С проведемо пряму КР, паралельну стороні АВ. Утворені кути АСК і ВСР позначимо цифрами 1 і 2. Тоді ∠A = ∠1, ∠B = ∠2, як внутрішні різносторонні кути при […]...

  20. Зовнішній кут трикутника та його властивості Розділ 3. Трикутники. Ознаки рівності трикутників § 18. Зовнішній кут трикутника та його властивості 438. ∠BAK – зовнішній кут при вершині А. 439. ∠LDP – зовнішній кут при вершині D. 441. ∠A + ∠B = 70° – за властивістю зовнішнього кута трикутника. 442. Зовнішній кут трикутника при вершині С дорівнює 74° згідно з властивістю зовнішнього […]...

  21. НЕРІВНОСТІ ТРИКУТНИКА РОЗДІЛ 3 ТРИКУТНИКИ & 15. НЕРІВНОСТІ ТРИКУТНИКА Ви вже знаєте, що кожна сторона трикутника менша від суми двох інших його сторін. Щоб довести це твердження як теорему, спочатку розглянемо іншу теорему. Теорема 19 У кожному трикутнику проти більшої сторони лежить більший кут, а проти більшого кута – більша сторона. Доведення. 1) Нехай у трикутнику ABC […]...

  22. Властивості подібних фігур Геометрія Подібність фігур Властивості подібних фігур Теорема. Коли фігура подібна фігурі , а фігура – фігурі , то фігури і Подібні. Із властивостей перетворення подібно­сті випливає, що у подібних фігур відповідні кути рівні, а відповідні відрізки пропорційні. Наприклад, у подібних трикутниках ABC і : ; ; ; . Ознаки подібності трикутників Теорема 1. Якщо два […]...

  23. ОЗНАКИ РІВНОСТІ ТРИКУТНИКІВ РОЗДІЛ 3 ТРИКУТНИКИ & 12. ОЗНАКИ РІВНОСТІ ТРИКУТНИКІВ Якщо трикутники ABC і А1В1С1 дорівнюють один одному, то їх можна сумістити. При цьому якщо сумістяться вершини А і А1, В і В1, С і C1, то сумістяться й сторони: АВ з A1B1, ВС з В1С1, СА з C1A1 і кути: ∠A з ∠A1∠B з∠B1, ∠C, ∠C1. […]...

  24. Ознаки рівності трикутників Геометрія Основні властивості найпростіших геометричних фігур Ознаки рівності трикутників Теорема 1 (перша ознака рівності трикутників – за двома сторонами й кутом між ­ними). Якщо дві сторони й кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні. Теорема 2 (друга ознака рівності трикутників – за стороною […]...

  25. Теореми про рівність і подібність трикутників – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Трикутник – де багатокутник із трьома сторонами. Сторони трикутника позначаються малими буквами, що відповідають позначенню протилежних вершин. Якщо всі три кути гострі – трикутник гострокутний. Якщо один з кутів прямий – прямокутний; сторони, що утворюють прямий кут, називаються катетами (а і b), сторона проти прямого кута – гіпотенузою (с). Якщо […]...

  26. Властивості й ознака рівнобедреного трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 12. Властивості й ознака рівнобедреного трикутника 476. На мал. 72: ML і МК – бічні сторони, KL – основа, ∠K = ∠L. 477. KD = DF, КЕ = EF, ∠K = ∠F, ∠KDE = ∠FDE, ∠DEK = ∠DEF = 90°. 478. Щоб провести бісектрису, медіану і […]...

  27. ВІДПОВІДІ І ВКАЗІВКИ ВІДПОВІДІ І ВКАЗІВКИ 7. АB. 11. Так. 12. Не належить. 13. КР, РТ, КТ, РК, TP, ТК. 16. 4. 19. Можна. 21. 6. Hа 16,17 або 18 частин. 28. 20,5 см. 29. 8 см. 31.10 дм. 33. 1) 2 см; 6 дм; 20 км. 34. 21 см. 42. Так. 44. а) 5,9 см. 45. а) […]...

  28. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника Розділ 3. Трикутники. Ознаки рівності трикутників § 15. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника 351. 1) AT – висота трикутника ABC. 2) AN – медіана трикутника ABC. 3) АР – бісектриса трикутника? AВС. 352. Оскільки AK – висота, то ∠BKA = ∠CKA = 90°. 353. Оскільки АК – бісектриса, то ∠BAK = […]...

  29. Коло, вписане в трикутник Урок № 50 Тема. Коло, вписане в трикутник Мета: домогтися засвоєння учнями змісту поняття кола, що вписане в трикутник, теореми про це коло, схеми її доведення та наслідку з неї. Сформувати вміння: – відтворювати формулювання означення і теореми про вписане в трикутник коло; – за описом об’єктів розрізняти ті, в яких мова йде про коло, […]...

  30. ПРО РІВНІСТЬ ГЕОМЕТРИЧНИХ ФІГУР РОЗДІЛ 3 ТРИКУТНИКИ & 11. ПРО РІВНІСТЬ ГЕОМЕТРИЧНИХ ФІГУР На малюнку 139 зображено два трикутники. Уявіть, що один із них накреслений на папері, а інший – на прозорій плівці. Переміщаючи плівку, другий трикутник можна сумістити з першим. Кажуть: якщо дані трикутники можна сумістити накладанням, то вони – рівні. Рівними один одному бувають не тільки трикутники, […]...

  31. Вправи 225-273 225. L ⊥ AB; X – точка прямої l; О – середина AB. ?АОХ = ?BOX (за першою ознакою рівності трикутників). 1) АО = OB; 2) ∠3 = ∠4 = 90°; 3) ОХ – спільна сторона. З цього випливає АХ = ВХ, отже, точка X рівновіддалена від кінців відрізка А і В. 226. Три прямі […]...

  32. Дотична до кола, її властивості Розділ 4. Коло і круг. Геометричні побудови § 22. Дотична до кола, її властивості 607. Проведемо радіус ОР, а потім за допомогою косинця побудуємо пряму m, перпендикулярну до радіуса. За теоремою 2 пряма m є дотичною до кола. 608. Проведемо радіус ОМ, а потім за допомогою косинця побудуємо пряму n, перпендикулярну до радіуса. За теоремою […]...

  33. Властивості кутів трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 10. Властивості кутів трикутника 344. ∠E = 60°, ∠F = 40°, ∠D = 80°. ∠E + ∠F + ∠D = 60° + 40° + 80° = 180°. 345. На мал. 208 неправильно сказано градусну міру кутів? АВС, оскільки? ABC – прямокутний, a ∠B + ∠C = […]...

  34. Третя ознака рівності трикутників Урок № 26 Тема. Третя ознака рівності трикутників Мета: домогтися розуміння учнями змісту третьої ознаки рівності трикутників та ідеї її доведення; формувати первинні вміння застосовувати третю ознаку рівності трикутників для розв’язування задач. Тип уроку: засвоєння знань. Наочність і обладнання: набір демонстраційного креслярського приладдя; таблиця “Ознаки рівності трикутників” (див. урок № 17). ХІД УРОКУ I. Організаційний […]...

  35. Прямокутний паралелепіпед. Піраміда Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 3. МНОЖЕННЯ І ДІЛЕННЯ НАТУРАЛЬНИХ ЧИСЕЛ 22. Прямокутний паралелепіпед. Піраміда Рис. 153 Коли ви були маленькими і гралися кубиками, то, можливо, складали фігури, зображені на рисунку 153. Ці фігури дають уявлення про прямокутний паралелепіпед. Форму прямокутного паралелепіпеда мають, наприклад, коробка цукерок, книга, цеглина, коробка сірників, пакувальний […]...

  36. Рівність трикутників Урок № 28 Тема. Рівність трикутників Мета: перевірити рівень засвоєння знань та сформованості вмінь учнів з теми. Тип уроку: контроль знань, умінь. Форма проведення: фронтальна контрольна робота. ХІД УРОКУ I. Організаційний момент II. Перевірка домашнього завдання Учитель збирає на перевірку зошити учнів із виконаною домашньою контрольною роботою. III. Умова контрольної роботи Варіант 1 Початковий рівень […]...

  37. Теореми § 2. Трикутники 11. Теореми 269. Теорема Умова Висновок 4.1 Кути АОС і СОВ – суміжні ∠AOC + ∠COB = 180° 8.2 X належить серединному перпендикуляру відрізка AB ХА = ХВ 9.1 ?ABC – рівнобедрений з основою АС 1) ∠A = ∠C; 2) бісектриса кута В є медіаною і висотою 10.3 Два кути трикутника ABC […]...

  38. Рівнобедрений трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівнобедрений трикутник Трикутник називається Рівнобедреним, якщо у нього дві сторони рівні. Ці сторони називаються Бічними сторонами, а третя сторона – Основою трикутника. На рисунку: ABC – рівнобедрений трикутник; – бічні сторони; AC – основа. Теорема 1. У рівнобедреному трикутнику кути при основі є рівними. Теорема 2. У рівнобедреному трикутнику […]...

  39. Рівносторонній трикутник – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Рівносторонній трикутник Усі висоти, медіани й бісектриси мають однакову довжину. Вписане і описане коло мають спільний центр. Середня лінія трикутника – відрізок, що сполучає середини двох сторін трикутника. Теорема: Зовнішній кут трикутника – кут, суміжний із внутрішнім кутом трикутника. Теорема: Теорема косинусів: у будь-якому трикутнику зі сторонами а, b, с […]...

  40. Тематична контрольна робота № 7 УРОК № 60 Тема. Тематична контрольна робота № 7 Мета уроку: перевірка навчальних досягнень учнів з курсу геометрії. Тип уроку: контроль навчальних досягнень учнів. Вимоги до рівня підготовки учнів: застосовують означення та властивості фігур при розв’язуванні задач. Хід уроку І. Тематичне оцінювання № 7 Тематичне оцінювання № 7 можна провести у вигляді тематичної контрольної роботи. […]...

Ви зараз читаєте: ПРЯМОКУТНИЙ ТРИКУТНИК
«
»