Рівняння прямої
УРОК № 28
Тема. Рівняння прямої
Мета уроку: виведення рівняння прямої. Формування вмінь учнів використовувати рівняння прямої до розв’язування задач.
Тип уроку: комбінований.
Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13].
Вимоги до рівня підготовки учнів: записують і пояснюють рівняння прямої. Розпізнають рівняння прямої.
Хід уроку
I. Перевірка домашнього завдання
Перевірити наявність виконаних домашніх завдань та відповісти на запитання, які виникли в учнів під час їх
ІІ. Аналіз результатів самостійної роботи
ІІІ. Сприйняття й усвідомлення нового матеріалу
Доведемо, що будь-яка пряма в декартових координатах має рівняння ax + by + c = 0, де а, b, с – деякі числа, а х і у – змінні координати точки А(х; у), яка належить прямій.
Як і при складанні рівняння кола, звернемося до такої властивості прямої, які мають точки цієї прямої, тобто: точки, які рівновіддалені від двох даних точок В і С, лежать на прямій (серединному перпендикулярі до відрізка ВС), яка перпендикулярна до ВС і проходить через середину відрізка ВС.
Нехай h – довільна пряма на площині і А(х; у) –
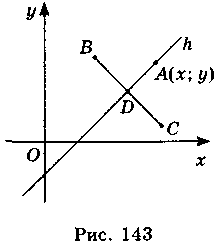
Спростимо цю рівність:
Х2 – 2ха1 +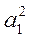 
+ у2 – 2yb1 + 
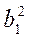= х2 – 2ха2 + 
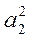+ у2 – 2уb2 + 
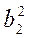, або -2хa1 + 2ха2 – 2yb1 + 2yb2 + 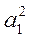+ 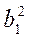– – 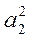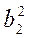= 0,
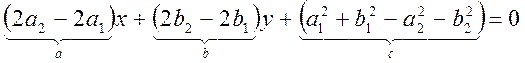, тоді маємо
Ax + by + с = 0, де а = 2а2 – 2а1, b = 2b2 – 2b1, c = + – – .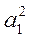
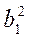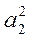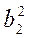Отже, рівняння прямої має вигляд ах + bу + с = 0, де a, b, c – деякі числа.
Розв’язування вправ
1) Знайдіть координати точок перетину з осями координат прямої:
А) 2х – 3y = 6;
Б) -3х – 7у = 21;
В) 4х + 3y – 12 = 0.
2) Пряма задана рівнянням 2х + у – 1 = 0. Які з точок А(0; 0), В(1; -1), С(0; 1), D(1; 0) належать прямій, а які не належать їй? 3) Побудуйте прямі:
А) 2x – y + l = 0;
Б) – х + 2у + 2 = 0;
В) х + у – 1 = 0.
IV. Закріплення й осмислення нового матеріалу
Розв’язування задач
1. Запишіть пряму, що проходить через точку А(3; 4), яка:
а) паралельна осі Ох;
Б) паралельна осі Оу;
В) проходить через початок координат.
2. Відомо, що пряма у – ах – 3 = 0 проходить через точку А(-1; 1). Знайдіть значення а. 3. Запишіть рівняння прямої АВ, якщо А(2; 3), В(3; 2).
Розв’язання
Оскільки шукана пряма ах + bу + с = 0 проходить через точки А і В, то
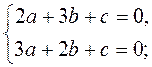
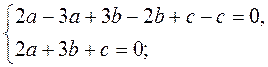
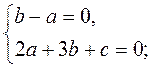
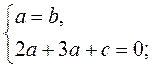
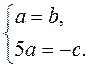
Нехай с = -5, тоді а = 1, b = 1. Отже, х + у – 5 = 0 – рівняння шуканої прямої.
Відповідь, х + у – 5 = 0.
4. Кінці діаметра А і В кола мають координати А(-3; 2), В(1; 7). Складіть рівняння прямої, що проходить через центр кола і перпендикулярна до діаметра. (Відповідь. 8х + 10y – 37 = 0) 5. Доведіть, що коло (х + 2)2 + (y – 3)2 = 52 має з прямою х – 2у = 6 дві спільні точки. Знайдіть ці точки. (Відповідь. (4; -1) і (-2,4; -4,2))
V. Домашнє завдання
1. Вивчити рівняння прямої. 2. Розв’язати задачі. 1) Скласти рівняння прямих, які проходять через точки:
А) А(0; 0) і В(1; 1);
Б) A(-3; 2) і В(-2; 1).
2) Побудувати прямі:
А) х + 2у – 3 = 0;
Б) х – 5 = 0;
В) 2у + 4 = 0.
VI. Підбиття підсумків уроку
Завдання класу
1. Запишіть рівняння прямої в загальному вигляді. Які дані треба знати, щоб записати рівняння прямої? Запишіть рівняння прямої, якщо а = -2, b = 3, с = 6. 2. Визначте, як розташована на координатній площині пряма:
А) x + 5 = 0;
Б) y – 1 = 0;
В) х = 0;
Г) y = 0.
(1 votes, average: 5.00 out of 5)
Loading...