Ромб. Квадрат
Урок № 9
Тема. Ромб. Квадрат
Мета: працювати над засвоєнням учнями змісту означень, властивостей та ознак ромба і квадрата. Формувати вміння:
– відтворювати вивчені твердження;
– застосовувати властивості, ознаки ромба і квадрата до розв’язування типових задач;
– застосовувати властивості, ознаки ромба і квадрата разом із раніше вивченими твердженнями в темі “Чотирикутники” до розв’язування задач підвищеного рівня складності.
Тип уроку: засвоєння вмінь та навичок.
Наочність та обладнання: конспект
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Перевірку засвоєння учнями теоретичного матеріалу попереднього уроку можна провести або у формі математичного диктанту, або у формі бесіди за тими самими питаннями, що включені в математичний диктант.
Математичний диктант
Варіант 1
1. Чи є прямокутником паралелограм, один із кутів якого прямий?
2. Чи правильно, що кожен прямокутник є паралелограмом?
3. Діагоналі прямокутника АЕКМ перетинаються в точці О. Відрізок АО дорівнює 3 дм. Знайдіть довжину діагоналі ЕМ.
4. Діагоналі чотирикутника
Варіант 2
1. Чи обов’язково чотирикутник з прямим кутом є прямокутником?
2. Чи правильно, що кожен паралелограм є прямокутником?
3. Діагоналі паралелограма мають довжину 3 дм і 5 дм. Чи цей паралелограм є прямокутником?
4. Сума довжин діагоналей прямокутника дорівнює 13 м. Знайдіть довжину кожної діагоналі.
@ Перед виконанням математичного диктанту слід нагадати учням правила виконання його завдань, а саме: умова завдань не записується (учні мають записати тільки номер запитання), відповідь має бути короткою, але змістовною (тобто у відповіді має бути аргументація – посилання на відповідне геометричне твердження).
Письмова частина домашнього завдання докладно перевіряється тільки в учнів, які потребують додаткової педагогічної уваги; у ході фронтальної перевірки правильності виконання письмових завдань достатньо озвучити твердження, яке було використане під час розв’язування задачі, а також здобуту відповідь.
III. Формулювання мети і завдань уроку
Щоб створити умови для усвідомленого сприйняття учнями логіки вивчення матеріалу, пропонуємо їм проаналізувати, яким чином із довільного паралелограма утворилась нова фігура – прямокутник (якщо всі кути паралелограма “зробити” рівними, то “виходить” прямокутник). Далі вчитель ставить запитання: “Які ще елементи паралелограма можна зробити рівними?” Звісно, більшість учнів дає правильну відповідь (сторони). Після чого формулюється наступне запитання: “Чи існує паралелограм, у якого і сторони, і кути рівні?” Здобувши ствердну відповідь, учитель виділяє таким чином два нові (тобто такі, що раніше не вивчались на уроках геометрії) геометричні об’єкти. Вивчення означення, властивостей та, можливо, ознак цих фігур, опанування способами їх застосування є основною дидактичною метою уроку.
IV. Актуалізація опорних знань та вмінь
З метою свідомого розуміння та подальшого засвоєння змісту означень, властивостей, ознак ромба і квадрата слід активізувати знання і вміння учнів щодо означення, властивостей та ознак паралелограма, прямокутника; означення, властивостей та ознак рівнобедреного трикутника.
Досягненню цієї мети сприятиме розв’язування усних задач.
Виконання усних вправ
1. Яких помилок припустилися під час зображення паралелограма (рис. 1)?
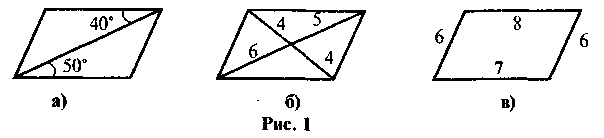
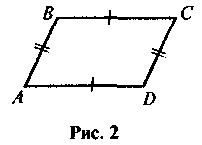
2. У чотирикутнику ABCD AB = DC, AD = BC (рис. 2). Доведіть, що ABCD – паралелограм.
3. У паралелограмі ABCD AM – бісектриса кута А, ВН – бісектриса кута В (рис. 3). Доведіть, що ВН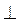 АМ.
АМ.
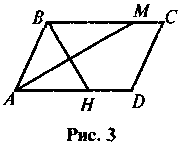
4. У паралелограмі ABCD через точку перетину діагоналей проведено відрізок, кінці якого лежать на його сторонах (рис. 4). Доведіть, що ОМ = ОК.
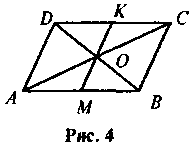
V. Засвоєння знань
План вивчення нового матеріалу
1. Означення ромба.
2. Властивості ромба.
3. Ознаки ромба.
4. Квадрат: означення, властивості.
@ Розглядаючи питання про означення прямокутника й ромба, слід звернути увагу учнів на той факт, що оскільки названі фігури є різновидами паралелограма, то й означення цих фігур дається через поняття паралелограма (тобто мова йде про формулювання означень через споріднене поняття); таким чином ми попереджаємо традиційні помилки учнів, яких вони припускаються, формулюючи означення прямокутника (ромба) як чотирикутника, у якого… (далі йде перелік певних ознак). Означення квадрата також формулюється за цим принципом, але на відміну від прямокутника та ромба, для яких безпосередньо спорідненим є поняття паралелограма, означення квадрата формулюється через поняття або ромба (в якого всі кути прямі), або через поняття прямокутника (в якого всі сторони рівні). При цьому завертаємо увагу учнів на еквівалентність цих обох означень.
Вивчаючи властивості ромба і квадрата, так само як і під час розгляду питання про властивості прямокутника, слід зробити акцент на тому, що із самих означень цих фігур випливає більшість їх властивостей (для ромба – це всі властивості паралелограма, а для квадрата – це всі властивості і прямокутника, а отже й паралелограма та ромба). Тому все, що слід зробити на цьому етапі вивчення матеріалу, – це сформулювати вивчені властивості, адаптувавши їх для названих фігур (зрозуміло, що доводити ці властивості не треба).
Інша річ, “додаткові” властивості та ознаки ромба.
1. Якщо всі сторони чотирикутника рівні, то цей чотирикутник – ромб.
2. Якщо сусідні сторони паралелограма рівні, то цей паралелограм – ромб.
3. Паралелограм із перпендикулярними діагоналями є ромбом.
4. Якщо діагональ паралелограма є бісектрисою його протилежних кутів, то цей паралелограм – ромб.
Оскільки вони є специфічними (тобто виконуються тільки для ромба), то необхідно їх довести (доведення можна провести за підручником або запропонувати учням виконати його самостійно, або запропонувати в якості індивідуального завдання для сильних учнів).
Повний перелік тверджень, які слід вивчити з восьмикласниками стосовно ромба і квадрата, вміщено в конспекті “Ромб. Квадрат”.
Конспект 4
Ромб
Означення. Паралелограм, усі сторони якого рівні, називається ромбом
Властивості
Ознаки
1. Має всі властивості паралелограма, тобто:
1)  А =
А =  С,
С,  В =
В =  D;
D;
2) АО = ОС, ВО = OD
1. Якщо ABCD – чотирикутник і AB = BC= CD = AD, то ABCD – ромб
2. Якщо A BCD – ромб, АС і BD – діагоналі, то:
1) AC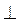 BD,
BD,
2)  OAD =
OAD =  OAB;
OAB;  ODA =
ODA =  ODC
ODC
2. Якщо ABCD – паралелограм і АВ = ВС, то ABCD – ромб
3. Якщо ABCD – паралелограм і AC1BD, то ABCD – ромб
4. Якщо ABCD – паралелограм і АС – бісектриса кутів А і С, то ABCD – ромб
Квадрат
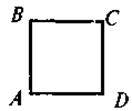
Означення. Прямокутник, усі сторони якого рівні, називається квадратом.
Означення. Ромб, усі кути якого прямі, називається квадратом
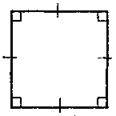
Властивості
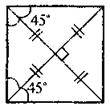
Має всі властивості прямокутника і ромба
VI. Формування первинних умінь
Виконання усних вправ
1. Назвіть види паралелограмів, у яких: а) усі кути рівні; б) усі сторони рівні; в) діагоналі рівні; г) діагоналі перпендикулярні.
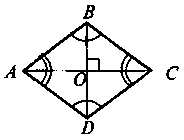
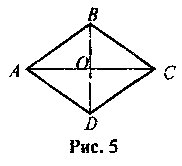
2. Діагоналі ромба ABCD перетинаються в точці О (рис. 5). Назвіть: а) бісектрису трикутника ABD; б) висоту трикутника ABC; в) медіану трикутника BCD.
3. Діагоналі квадрата A BCD перетинаються в точці О. Назвіть усі рівні трикутники, які утворюються при перетині діагоналей. Визначте її вид.
Виконання графічних вправ
1. Накресліть дві перпендикулярні прямі, які перетинаються в точці О. На одній з прямих відкладіть по різні боки від точки О рівні відрізки ОА і ОС, а на другій прямій – рівні відрізки ОВ і OD. Сполучіть точки A, B, C і D.
А) Виміряйте сторони чотирикутника ABCD і визначте його вид.
Б) Виміряйте кут А чотирикутника ABCD. Користуючись властивостями цього чотирикутника, знайдіть градусні міри інших його кутів. Перевірте результати вимірюванням.
В) Виміряйте кути ADB і CDB. Виділіть кольором усі пари рівних кутів між діагоналями і сторонами чотирикутника.
2. Накресліть прямокутний трикутник ABD з гіпотенузою BD. Проведіть через вершини В і D прямі, паралельні сторонам AD і АВ відповідно. Позначте точку С – точку перетину цих прямих.
А) Виміряйте сторони чотирикутника ABCD і визначте його вид.
Б) Проведіть діагональ АС. Виміряйте і порівняйте довжини діагоналей чотирикутника.
В) Позначте на прямих ВС і AD точки С1 і D1 так, щоб чотирикутник ABC1D1 був квадратом.
Виконання письмових вправ
1. Знайдіть кути ромба, якщо:
А) один із них на 120° більший за інший;
Б) одна з його діагоналей дорівнює стороні.
2. Знайдіть кути ромба, якщо:
А) кути, утворені його стороною з діагоналями, відносяться як 1 : 4;
Б) висота ромба удвічі менша від сторони.
3. Периметр квадрата дорівнює 40 м. Знайдіть відстань від точки перетину діагоналей квадрата до його сторони.
4*. У рівнобедрений прямокутний трикутник вписано квадрат, дві вершини якого лежать на гіпотенузі трикутника, в дві інші – на катетах. Знайдіть периметр квадрата, якщо гіпотенуза дорівнює 18 см.
VII. Підсумки уроку
1. Які спільні властивості мають ромб і квадрат?
2. Які властивості квадрата не характерні для прямокутника?
3. Чи є квадратом:
А) прямокутник ABCD, діагональ AC якого є бісектрисою кута BAD;
Б) ромб, діагоналі якого рівні;
В) паралелограм, діагоналі якого взаємно перпендикулярні;
Г) чотирикутник, усі сторони якого рівні?
VIII. Домашнє завдання
Вивчити зміст означення, властивостей та ознак ромба і квадрата.
Розв’язати задачі.
1. Знайдіть кути ромба, якщо:
А) сума двох із них дорівнює 220°;
Б) діагональ утворює з однією зі сторін кут 25°.
2. Відстань між протилежними сторонами квадрата дорівнює 5 см. Знайдіть периметр квадрата.
3. Знайдіть кути ромба, якщо висота, проведена з вершини тупого кута, відтинає від ромба рівнобедрений трикутник.
Повторити вивчений матеріал. Побудувати схему, що відображається зв’язок між чотирикутниками, паралелограмами, прямокутниками, ромбами та квадратами.
