Розв’язання задач за допомогою систем рівнянь
973. Нехай 1 кг помідорів коштує x грн, а 1 кг огірків – у грн. Складаємо систему рівнянь:
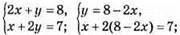
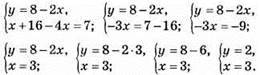
Відповідь: 3 грн.; 2 грн.
974. Нехай 1 альбом коштує x грн., а 1 зошит у грн. Складаємо систему рівнянь:
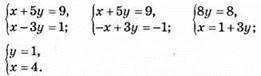
Відповідь: альбом коштує 4 грн., зошит – 1 грн.
975. Нехай маса 1 ящика слив x кг, а 1 ящика винограду – у кг. Складаємо систему рівнянь:
Відповідь: 8 кг; 7 кг.
976. Нехай вантажність одного автомобіля буде х т, а другого – у т. Складаємо
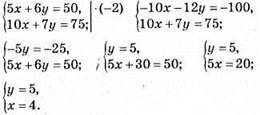
Відповідь: 4 т і 5 т.
977. Нехай числа будуть x і у.
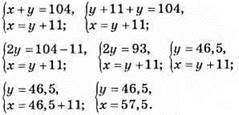
Відповідь: 57,5 і 46,5.
978. Нехай числа будуть х і у.
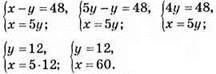
Відповідь: 12 і 60.
979. Нехай х було двомісних і у тримісних човнів.
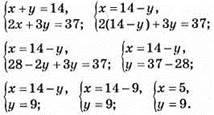
Відповідь: 5 двомісних; 9 тримісних човнів.
980. Нехай на теплоході х двомісних і у чотиримісних кают.
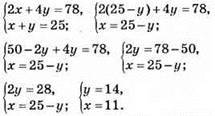
Відповідь: 11 двомісних, 14 чотиримісних кают.
981.
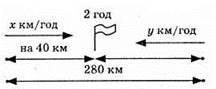
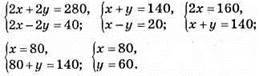
Відповідь: 80 км/год, 60 км/год.
982. Нехай перший робітник за
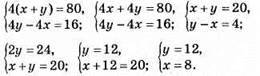
Відповідь: 8 деталей, 12 деталей.
Рівень Б
983. Нехай на першій полиці стояло х книг, а на другій – у книг.
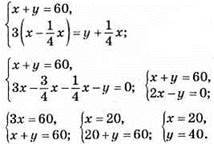
Відповідь: 20 і 40 книжок.
984. Нехай на першій гілці було х горобців, а на другій – у горобців.
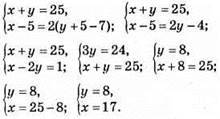
Відповідь: 17 і 8 горобців.
985. Нехай швидкість теплохода у стоячій воді х км/год, а швидкість течії річки у км/год, тоді швидкість теплохода за течією (х + у) км/год, а проти течії – (х – у) км/год.
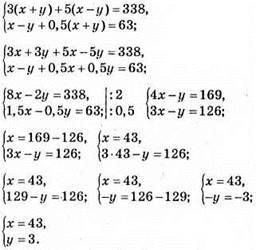
Відповідь: 43 км/год; 3 км/год.
986. Нехай швидкість теплохода у стоячій воді x км/год, а швидкість течії річки у км/год, тоді швидкість теплохода за течією (х + у) км/год, а проти течії – (x – у) км/год.
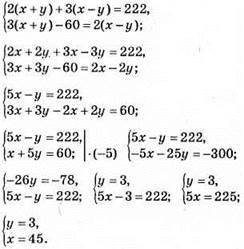
Відповідь: 45 км/год; 3 км/год.
987. Нехай було x палок і летіло у галок.
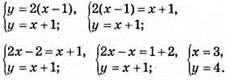
Відповідь: 3 палки, 4 галки.
988. Нехай кінь ніс x мішків, а мул – у мішків.
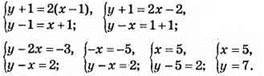
Відповідь: 5 і 7 мішків.
989. Нехай x тис. грн. на першому рахунку і у тис. грн. – на другому.
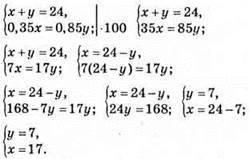
Відповідь: 17 тис. грн., 7 тис. грн.
990. Нехай на першому складі було x т цукру, а на другому – у т цукру.
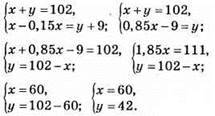
Відповідь: 60 т, 42 т.
991. Нехай число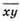 
має x десятків і у одиниць.
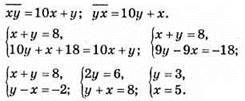
Відповідь: 53.
992. Нехай швидкість туриста, що вийшов з пункту А в пункт В, буде x км/год, а швидкість туриста, що вийшов з пункту В до пункту А – у км/год.
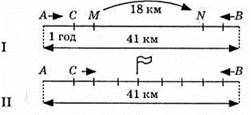
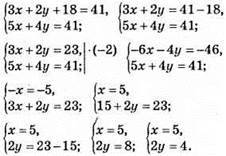
Відповідь: 5 км/год, 4 км/год.
993.
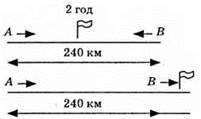
Нехай швидкість автомобіля, що вирушає з пункту А х км/год, а швидкість автомобіля, що вирушає з пункту В – у км/год.
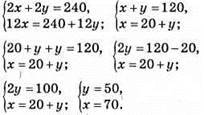
Відповідь: 70 км/год, 50 км/год.
Рівень В
994. Нехай х і у числа.
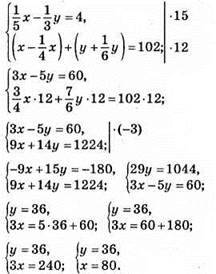
Відповідь: 80, 36.
995. Нехай місткість першої посудини х л, другої – у л, з другої посудини вилили z л, а з першої – w л.
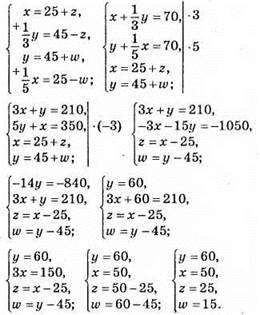
Відповідь: 50 л, 60 л.
996. Нехай початкова ціна акції підприємства A х грн., а підприємства В – y грн.
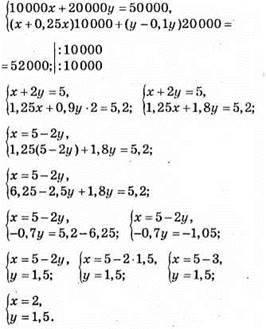
Відповідь: 2 грн.; 1,5 грн.
997. Нехай антикварний магазин купив два предмети за х грн. і у грн.
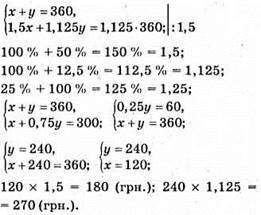
Відповідь: 180 грн.; 270 грн.
998. Нехай у двоцифрового числа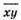 
х десятків і у одиниць.
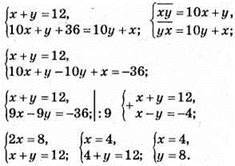
Відповідь: 48.
999.
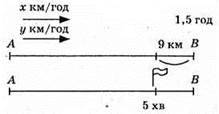
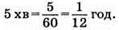
Нехай х км/год – швидкість першого мотоцикліста і у км/год – другого.
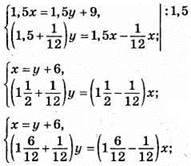
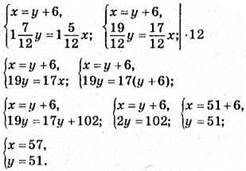
S = 1,5x = 1,5 • 57 = 85,5 км.
Відповідь: 57 км/год; 51 км/год; 85,5 км.
1000. Нехай довжина шосе х км, а грунтової дороги – у км.
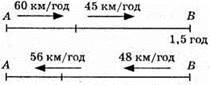
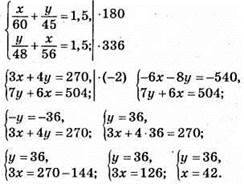
Відповідь: 42 км; 36 км.
1001.
Vза течією = 10 + 2 = 12 км/год.
Vпроти течії = 10 – 2 = 8 км/год.
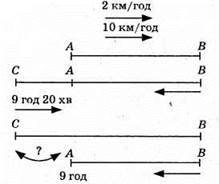
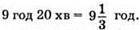
Нехай відстань між пристанями А i С буде x км, a між А i В – у км.
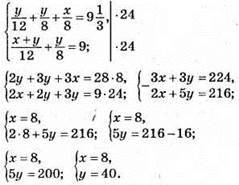
Відповідь: 8 км.
Вправи для повторення
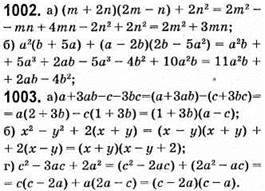
1004. a) 7253 – 3753 = (725 – 375) • (7252 + 725 • 375 + 3752) = 350 • (7252 + 725 х 375 + 3752) ділиться на 350;
Б) 723 + 883 = (72 + 88) • (722 – 72 • 88 + 882) = 160 • (722 – 72 • 88 + 882) ділиться на 80.
1005. Х2 – 4Х + у2 – 4у + 9 = 0;(Х2 – 4Х + 4) + (y2 – 4y + 4) + 1 = 0; (х – 2)2 + (y – 2)2 + 1 = 0. Сума квадратів дає найменше число 0, 0 + 1 ≠ 0. Не існує чисел х та у, для яких виконувалася б рівність х2 – 4х + у2 – 4у + 9 = 0.
1006. у = 1/2х + 2;
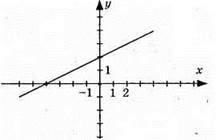
X | 0 | 2 |
У | 2 | 3 |
(-4; 0) і (0; 2) – точки перетину з осями координат.
(1 votes, average: 5.00 out of 5)
Loading...