Головна ⇒ 📌Математика ⇒ Розв’язування рівнянь. Основні властивості рівняння

Розв’язування рівнянь. Основні властивості рівняння

Розділ 4 Раціональні числа і дії мідними

§48. Розв’язування рівнянь. Основні властивості рівняння

До цього часу ми розв’язували рівняння, використовуючи залежності між компонентами дій. Розглянемо основні властивості рівняння, що нададуть можливість значно спростити процес розв’язування знайомих нам видів рівнянь та навчитися розв’язувати нові види рівнянь.

Приклад 1. Розв’язати рівняння 3 ∙ (x + 2) = 18.

Розв’язання. За правилом знаходження невідомого множника маємо x + 2 = 18 : 3, x + 2 = 6. Це саме рівняння можна отримати,

якщо обидві частини початкового рівняння поділити на 3 або помножити обидві частини на

Розвязування рівнянь. Основні властивості рівняння

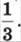
Закінчуючи розв’язування рівняння, знайдемо

X = 6 – 2; x = 4.

Число 4 є коренем як рівняння x + 2 = 6 (бо 4 + 2 = 6), так і коренем рівняння 3 ∙ (x + 2) = 18 (бо 3 ∙ (4 + 2) = 18). Маємо таку властивість рівняння:

– корені рівняння не зміняться, якщо його обидві частини помножити або поділити на одне й те саме відмінне від нуля число.

Приклад 2. Розв’язати рівняння x + 2 = 7.

Розв’язання. За правилом знаходження невідомого доданка маємо x = 7 – 2. Це рівняння можна одержати з початкового, якщо перенести

доданок 2 з лівої частини в праву, змінивши знак цього доданка на протилежний (з “+” на “-“). Остаточно маємо x = 5.

Приклад 3. Розв’язати рівняння x – 3 = 8.

Розв’язання. За правилом знаходження невідомого зменшуваного маємо x = 8 + 3. Це рівняння можна одержати з початкового, якщо перенести доданок -3 з лівої частини в праву, змінивши знак доданка на протилежний (з “-” на “+”). Отже, x = 11 – корінь рівняння.

Маємо ще одну властивість рівняння:

– корені рівняння не зміняться, якщо деякий доданок перенести з однієї частини рівняння в іншу, змінивши при цьому його знак на протилежний.

Виходячи з наведених властивостей, складемо загальну схему розв’язування рівнянь, яку застосуємо в наступному прикладі.

Приклад 4. Розв’язати рівняння

4(x – 3) – 12x = 3(2 – x) + 7.

Розв’язання.

1	Розкриємо дужки	4х – 12 – 12х = 6 – 3х + 7
2	Зведемо подібні доданки в лівій і правій частинах рівняння	-8х – 12 = 13 – 3х
3	Перенесемо доданки, які містять невідоме, в одну частину рівняння (частіше в ліву), а решту доданків – у іншу частину рівняння, змінивши при цьому їх знаки на протилежні	-8х + 3х = 13 + 12
4	Зведемо подібні доданки в лівій та правій частинах рівняння	-5х = 25
5	Знайдемо корінь рівняння	Х = 25 : (-5) Х = -5
6	Перевірка (бажано)	Ліва частина 4(-5 – 3) – 12 ∙ (-5) = 28 права частина 3(2 – (-5)) + 7 = 28

А ще раніше…

У “геометричній алгебрі” давніх греків розв’язати рівняння означало побудувати відрізок, що дорівнює додатному кореню рівняння.

Паростки нової “арифметичної алгебри” зустрічаються у Діофанта. Зоокрема в “Арифметиці” він розглядає таку задачу.

Задача Діофанта. Якщо додати до 20 і відняти від 100 одне й те саме число, то отримана сума буде в 4 рази більшою за отриману різницю. Знайти невідоме число.

Спробуй розв’язати цю задачу!

Майже 4 тисячі років тому в Давньому Єгипті вже розв’язували найпростіші рівняння.

Другу з розглянутих у цьому параграфі властивостей рівнянь вперше відкрив арабський математик Мухаммед аль-Хорезмі (783 – близько 850), автор грунтовної роботи “Кітаб аль-Джебр аль-Мукабала” (“Книга про відновлення та протиставлення”). Називав аль-Хорезмі цю властивість аль-джебр, тобто “відновлення”.

Сформулюй основні властивості рівняння. Як перенести доданки з однієї частини рівняння в іншу?

1324. (Усно) Чи є число -3 коренем рівняння:

1) x + 2 = 1; 2) x ∙ 7 = -21; 3) x – 2 = -5; 4) x : 3 = 1?

1325. Чи є число -8 коренем рівняння:

1) x + 6 = -2; 2) 3 – x = -5; 3) 4 ∙ x = 32; 4) 16 : x = -2?

1326. (Усно) Знайди корінь рівняння:

1) x – 7 = 8; 2) 2 + x = 1; 3) x ∙ 5 = -10; 4) x : 2 = -3.

1327. (Усно) Чи правильно перенесено доданки в таких рівняннях:

1) 5x + 7 = x, 2) -4x + 9 = 2x, 5x – x = 7; -4x – 2x = -9;

3) -2x – 7 = -3x + 9,

4) 7x – 2 = 2x – 3, -2x + 3x = 9 + 7; 7x – 2x = -3 – 2?

1328. Перенеси з лівої частини рівняння в праву доданок, який не містить невідомого:

1) 4x + 2 = 7; 2) -5x – 3 = 9;

3) 3x – 9 = 0; 4) -7x + 2 = 3.

1329. Перенеси з правої частини рівняння в ліву доданок, який містить невідоме:

1) 3x = 5 – 2x; 2) 7 m = -5 + 2m;

3) -3y = 4 – 5y; 4) -7p = 2p + 7.

1330. Збери в лівій частині рівняння всі доданки, що містять невідоме, а в правій – усі доданки, які не містять невідомого:

1) 9x + 5 = 7 – 5x; 2) 4m – 2 = 5m + 3;

3) -4y – 7 = -2y + 9.

1331. Збери в лівій частині рівняння всі доданки, які містять невідоме, а в правій – усі доданки, які не містять невідомого:

1) -3x + 7 = 8 – 2x; 2) 5y + 2 = -3y – 3;

3) -9p – 5 = 4p + 7.

1332. Чи є коренем рівняння 2(x + 7) = 8 число:

1) -2; 2) -3?

1333. Чи є коренем рівняння 5(x + 2) = -20 число:

1) -6; 2) -5?

1334. Знайди корінь рівняння:

1) 2х + 6 = 8; 2) 3 – 4у = -1; 3) -10 + 5m = 4;

4) 7х = 3х – 5; 5) -2т = 14 + 8т; 6) 3у = -5у + 16.

1335. Розв’яжи рівняння:

1) 3х + 10 = 16; 2) 2 – 3у = -4; 3) -5 + 2* = -7;

4) 5х = -8 + х; 5) -4у = 7 + 3у; 6) 8т = -2т + 9.

1336. Розв’яжи рівняння:

1) 5х + 3 = 4х + 8; 2) 3х -16 = 8х + 19;

3) 5 – 3х = 4 – 2х; 4) 0,8т + 2,4 = 0,4т – 1,6;

5) 0,17х – 1,8 = 0,18х + 1,2;

6) 0,8х + 1,16 = 0,9х – 1,8.

1337. Знайди корінь рівняння:

1) 6х + 12 = 5х + 3; 2) 7у – 11 = 10у + 16;

3) 3т + 7 = 6т – 2; 4) 4,6 + 0,6у = 0,3у – 2,3;

5) 0,27х – 3,8 = 0,28х + 5,2;

6) 0,7т + 1,98 = 0,8т – 4,4.

1338. Розв’яжи рівняння:

1339. Розв’яжи рівняння:

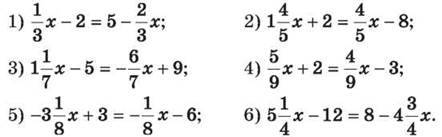
1340. Поясни кожний “крок” розв’язування рівняння:

1) 2(x – 3) = 5x,

2x – 6 = 5x,

2x – 5x = 6,

-3x = 6, x = 6 : (-3),

X = -2;

2) 3(4x – 1) = -7(x – 2),

12x – 3 = -7x + 14,

12x + 7x = 14 + 3,

19x = 17, x = 17 : 19,

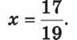
1341. Розв’яжи рівняння:

1) 2(x – 3) = 4x; 2) – ( 4x – 3) = – x;

3) -4(x + 5) = -16; 4) 3(x + 7) = 2(x – 8);

5) 4(-x + 7) = – (x + 2); 6) -3(2 – x) = 4(x + 9).

1342. Знайди корінь рівняння:

1) 3(x – 4) = 5x; 2) – ( 5x – 8) = – x;

3) -5(x + 2) = -15; 4) 7(x – 2) = 6(x + 1);

5) 3(-x + 2) = – (x – 8); 6) -5(7-x) = 6(x + 2).

1343. Розв’яжи рівняння:

1) 3(x – 2) = -10x; 2) – ( 2x – 5) = -5x;

3) -3(x – 3) = 7; 4) 5(x + 2) = 11(x – 3).

1344. Розв’яжи рівняння:

1) 4(x – 2) = -5x; 2) – ( 4x – 7) = -7x;

3) -6(x – 1) = 13; 4) 2(x + 1) = 9(x – 3).

1345. Знайди корінь рівняння:

1) 2(0,2x – 3) – 8(0,7x – 4) = 39;

2) 3,2(2 – 3y) = 3(0,8y – 1) + 3,4;

3) 3(0,4x + 7) – 4(0,8x – 3) = 2;

4) 0,3(2x – 1) – 0,9 = 0,2(5x – 2).

1346. Знайди корінь рівняння:

1) 5(0,3x + 6) – 4(0,2x – 7) = -5;

2) 0,5(3x – 4) + 4,4 = 0,9(4x – 2).

1347. Використовуючи основну властивість пропорції, розв’яжи рівняння:

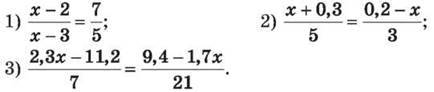
1348. Знайди корінь рівняння:

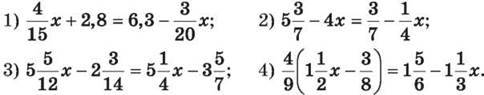
1349. Розв’яжи рівняння:

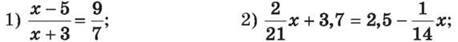
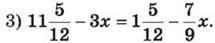
1350. При якому значенні x вирази 5(2 – x) і -3(5 + 2x) набувають рівних значень?

1351. При якому значенні y вирази 0,3(5y – 7) і 3(0,2y + 3,2) набувають рівних значень?

1352. Знайди корінь рівняння:

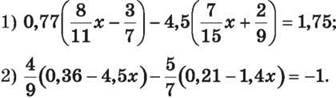
1353. Розв’яжи рівняння:

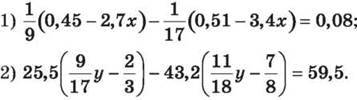
1354. При якому значенні а рівняння (а – 8)x = 5 + 3а має корінь, що дорівнює числу 2?

1355. Розв’яжи рівняння:

1) 2(x – 2) + x = 3(x – 1); 2) 4(x – 2) + 2x = 2(3x – 4).

1356. Обчисли значення виразу 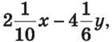якщо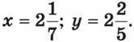

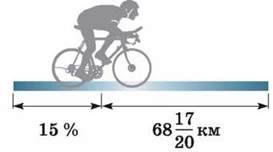
1357. Ц0 За першу годину велосипедист проїхав 15 % відстані, після чого йому залишилося проїхати ще 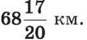Яку відстань мав проїхати велосипедист?

1358. До 120 г 10-відсоткового розчину солі долили 80 г води. Яка концентрація солі у новому розчині?

1359. Кожне ребро куба збільшили на 10 %. На скільки відсотків збільшилася площа його поверхні і на скільки відсотків збільшився його об’єм?

(1 votes, average: 5.00 out of 5)

Ви зараз читаєте: Розв’язування рівнянь. Основні властивості рівняння

« Компост – СЛОВНИК АГРОТЕХНІЧНИХ ТЕРМІНІВ

Українське анімаційне кіномистецтво »

Related posts: