Розв’язування задач координатно-векторним методом
1.
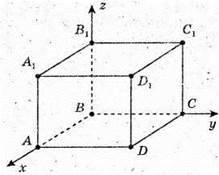
1) Введемо прямокутну систему координат із початком у точці В і спрямуємо вісь Оx вздовж ребра BA, Oz – вздовж ВВ1. Довжину ребра куба позначимо як а.
Тоді координати точок: А(а; 0; 0;); С(0; а; 0); R(а; а; 0); C1(0; а; а).
Знайдемо координати векторів 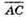 і
і 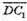
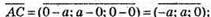
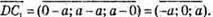
Знайдемо довжини векторів:
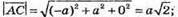
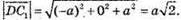
Знайдемо кут між векторами:
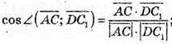
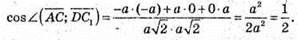
Кут між векторами 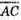 і
і 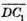 порівнює
порівнює 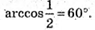
2) Введемо прямокутну систему координат із початком у точці В і
Спрямуємо вісь Ох вздовж ребра BА, Oz — вздовж BВ1.
Довжину ребра куба позначимо як а.
Тоді координати точок: А(а; 0; 0); D1(а; а; а); В(0; 0; 0); D(а; а; 0);
Знайдемо координати точки Р – середини ребра DD1:
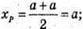
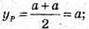
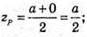
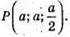
Знайдемо координати векторів 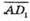 і
і 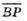
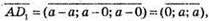
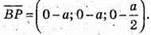
Знайдемо
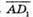 і
і 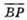 і скалярний добуток:
і скалярний добуток: 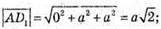
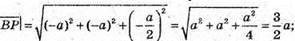
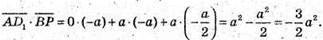
Знайдемо кут між векторами:
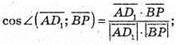
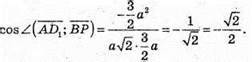
Кут між векторами 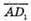 і
і 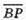 дорівнює
дорівнює 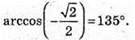
Відповідь: 1) 60°; 2) 135°.
2.
Введемо прямокутну систему координат із початком у точці В
І спрямуємо вісь Ох вздовж ребра ВА, Оz – вздовж ВВ1,
AB = a, AD = 2a, AA1 = 3a.
Координати точок: В(0; 0; 0); D(a; 2а; 0); А(а; 0; 0); В1(0; 0; За).
Знайдемо координати векторів 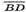 і
і 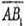
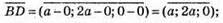
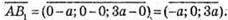
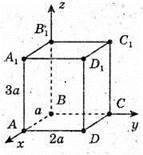
Знайдемо довжини векторів 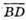 і
і 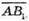 скалярний добуток:
скалярний добуток:
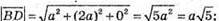
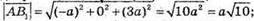
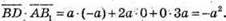
Знайдемо кут між векторами 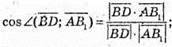
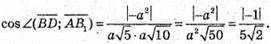
Оскільки кут між прямими не може бути тупим, то кут дорівнює 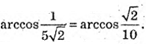
Відповідь; 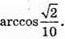
3.
Знайдемо кут ОАС.
Для цього знайдемо координати векторів 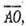 і
і 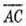 та їх скалярний добуток
та їх скалярний добуток
І довжини: 
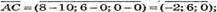
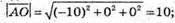
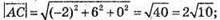
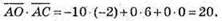
Тоді косинус кута між векторами 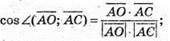
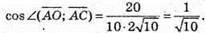
Скористаємось основною тригонометричною тотожністю cos2α + sin2α = 1, тоді
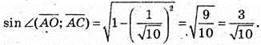
Відстань від точки А до прямої, що проходить через точки О і С,
Це висота трикутника ОАС. Позначимо її AH.
Площа трикутника виражається формулою 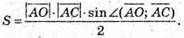
З іншого боку 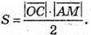
Знайдемо довжину вектора 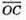 :
: 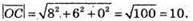
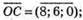
Маємо 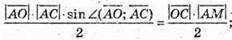
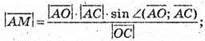
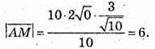
Відповідь: 6.
4.
Знайдемо координати векторів 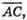
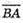
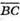
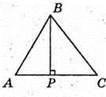
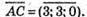
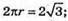
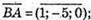
Знайдемо довжини векторів:
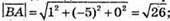
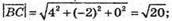
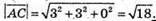
Та скалярний добуток 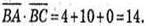
Знайдемо косинус кута ABC
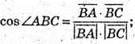
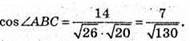
Скористаємось основною тригонометричною тотожністю
Cos2 α + sin2 α = 1
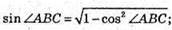
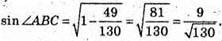
Площа ААВС: 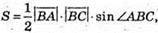 з іншого боку
з іншого боку 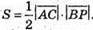
Маємо
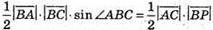
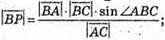
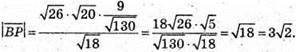
Відповідь: 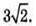




 (1 votes, average: 5.00 out of 5)
(1 votes, average: 5.00 out of 5)Related posts:
- Розв’язування задач на застосування векторів Урок 60 Тема. Розв’язування задач на застосування векторів Мета уроку: формування вмінь учнів застосовувати вивчений матеріал до розв’язування задач. Обладнання: стінна таблиця “Вектори в просторі”. Хід уроку І. Перевірка домашнього завдання 1. Два учні відтворюють розв’язування задач № 55 (4), 56. 2. Фронтальне опитування. 1) Чому дорівнює скалярний добуток векторів, які задано координатами? 2) Як […]...
- Кут між векторами. Скалярний добуток векторів Урок 59 Тема. Кут між векторами. Скалярний добуток векторів Мета уроку: формування понять кута між векторами, скалярного добутку векторів. Формування вмінь учнів застосовувати вивчений матеріал до розв’язування задач. Обладнання: схема “Вектори в просторі” Хід уроку 1. Фронтальна бесіда з класом за контрольними запитаннями № 18- 20 з використанням схеми “Вектори в просторі” (див. с. 233). […]...
- Скалярний добуток векторів Геометрія Вектори Скалярний добуток векторів Скалярним добутком векторів і називається число . Позначення: . . Очевидно, що . Розподільна властивість скалярного добутку: . Кутом між ненульовими векторами і називається кут BAC. Кутом між будь-якими двома ненульовими векторами і називається кут між векторами, що дорівнюють даним і мають спільний початок. Вважають, що кут між однаково напрямленими […]...
- Вектори в просторі – Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Вектори в просторі Усі основні означення векторів у просторі залишаються такими самими, як означення векторів на площині (див. розділ “Геометрія. 8 клас”). Координатами вектора , де , , називають числа, , . Вектори рівні тоді, й тільки тоді, коли вони мають відповідно рівні координати. Це дає підставу позначити […]...
- Координати вектора. Дії над векторами, що задані координатами 1. Запишемо координати вектора: 1) 2) 3) 4) 2. 1) 2) 3) 4) 5) 6) 3. 1) Запишемо розклад за координатними векторами: 2) Запишемо розклад за координатними векторами: 3) Запишемо розклад за координатними векторами: 4) Знайдемо координати векторів : Знайдемо координати вектора Запишемо розклад за координатними векторами: 5) Знайдемо координати векторів Знайдемо координати вектора Запишемо […]...
- Скалярний добуток векторів УРОК № 49 Тема. Скалярний добуток векторів Мета уроку: формування поняття скалярного добутку векторів; формування вмінь застосовувати вивчені означення та властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині”[13]. Вимоги до рівня підготовки учнів: формулюють означення скалярного добутку, його властивості; застосовують вивчені означення та властивості до розв’язування […]...
- Вектори у просторі – ВЕКТОРИ Формули й таблиці МАТЕМАТИКА ВЕКТОРИ Вектори у просторі Вектор – спрямований відрізок А – початок вектора В – кінець вектора Модуль вектора – довжина відрізка, який зображує вектор: ||. Два вектори рівні, якщо вони однаково спрямовані і мають рівні модулі. Координати вектора з початком у точці А(x1,y1,z1) і кінцем у точці В(х2,у2,z2). Рівні вектори мають […]...
- Векторний добуток векторів 1. Векторний добуток векторів є вектором, а скалярний – числом. Векторний та скалярний добуток мають однакові властивості (крім комутативності). 2. За означенням модуля векторного добутку А отже, оскільки то 3. 1) За означенням У нашому випадку Скористаємось основною тригонометричною тотожністю: Тоді 2) За означенням У нашому випадку Скористаємось основою тригонометричною тотожністю: Тоді Оскільки 3) Рівність […]...
- Розв’язання систем лінійних рівнянь способом підстановки Рівень А Відповідь: (1; 3). Відповідь: (7; -4,5). Відповідь: (1; 3). Відповідь: (4; 1). Відповідь: (3; 1). Відповідь: (1;-2). Відповідь: розв’язків немає. Відповідь: (3; 2). Відповідь: (4; 0). Відповідь: (3; 5). Відповідь: (1,5; 2). Відповідь: (3; -1). Відповідь: (7; 1). Відповідь: (1; -1). Рівень Б Відповідь: (2; 1,5). Відповідь: (1; -2). Відповідь: (20; 0,5). Відповідь: […]...
- Вектори в просторі (рівність векторів, колінеарність векторів, компланарність векторів). Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами Урок 58 Тема. Вектори в просторі (рівність векторів, колінеарність векторів, компланарність векторів). Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами Мета уроку: формування знань учнів про вектори в просторі, дії над векторами, заданими координатами, Формування вмінь застосовувати вивчений матеріал до розв’язування задач. Обладнання: схема “Вектори в просторі”. Хід уроку І. Перевірка домашнього […]...
- Розв’язування задач геометричного змісту Урок № 126 Тема. Розв’язання задач геометричного змісту 1. На координатній прямій позначте точку D(-3) і точку С, щоб довжина CD дорівнювала 2,5 одиничних відрізки. Визначте координату точки С. Скільки розв’язків має задача? 2. Знайдіть площу і периметр чотирикутника ABCD, якщо A(-1; 2); B(3; 2); С(3; -4); D(-1; -4). 3. Знайдіть площі заштрихованих фігур, зображених […]...
- Розв’язування систем лінійних рівнянь методом підстановки Відповідь: (2; 5). Відповідь: (-20; 6). Відповідь: (48; 8). Відповідь: (4; 2). Відповідь: (7; 3). Відповідь: (8; -6). Відповідь: (9; 3). Відповідь: (2; 3,8). 1035. Відповідь: (4; -4). Відповідь: (3; -1). Відповідь: (5; 4). Відповідь: (0,5; 4). Відповідь: (8; -1). Відповідь: (3; 5). 1036. Відповідь: (6; 3). Відповідь: (4; 2). Відповідь: (1; 2). Відповідь: (4; […]...
- Властивості призми 1. 2. 3. Ні, не можна. 4. Бічні ребра перпендикулярні до основи. Усі бічні грані – прямокутники. Бічне ребро є висотою призми. Площа бічної поверхні – добуток периметра Основи на довжину бічного ребра. 5. Так, може. Див. мал. до № 2. 6. 1) Основа правильної призми – правильний багатокутник, Усі бічні грані – рівні прямокутники. […]...
- Колінеарні вектори УРОК № 48 Тема. Колінеарні вектори Мета уроку: формування поняття “колінеарні вектори”; вивчення властивості та ознаки колінеарних векторів; формування вмінь учнів застосовувати вивчені означення та властивості до розв’язування завдань. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують колінеарність векторів; застосовують вивчені означення та […]...
- Розв’язування систем лінійних рівнянь методом додавання 1047. Відповідь: (7; -1). Відповідь: (3; 5). Відповідь: (4; -1/3). Відповідь: (-1; 10). Відповідь: (-1; 16). Відповідь: (2; -3). 1048. Відповідь: (4; -4). Відповідь: (2; 2). Відповідь: (1; 1). Відповідь: (2; -1). 1049. Відповідь: (8; 1). Відповідь: (1,2; 0). Відповідь: (-1; -2). Відповідь: (7; -1). Відповідь: (4; -1). Відповідь: (6; -2). Відповідь: u = 2, […]...
- Прямокутна система координат на площині УРОК № 22 Тема. Прямокутна система координат на площині Мета уроку: узагальнення та систематизація матеріалу про декартову прямокутну систему координат. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують прямокутну систему координат. Застосовують вивчені означення до розв’язування задач. Хід уроку I. Перевірка домашнього завдання […]...
- Віднімання векторів – Елементи векторної алгебри 3. Елементи векторної алгебри 3.3. Віднімання векторів Різницею двох векторів, спрямованих по одній прямій або паралельних один одному, є алгебраїчна різниця цих векторів. Щоб знайти різницю двох векторів, які мають різні напрями, треба розмістити обидва вектори так, щоб вони виходили з однієї точки. Потім сполучити кінці векторів вектором, спрямованим від від’ємника до зменшуваного. Цей вектор […]...
- Координати вектора УРОК № 43 Тема. Координати вектора Мета уроку: формування поняття координат вектора та вміння застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують координати вектора; застосовують вивчені означення і властивості до розв’язування задач. Хід уроку I. […]...
- Додавання векторів за правилом паралелограма – Елементи векторної алгебри 3. Елементи векторної алгебри 3.2. Додавання векторів за правилом паралелограма Щоб додати два вектори за правилом паралелограма, треба розмістити їх так, не змінюючи їх напряму, щоб вони виходили з однієї точки, й добудувати на кінцях векторів паралельні прямі. Діагональ одержаного паралелограма, проведена з точки, в якій суміщені початки обох векторів, є їх сумою....
- Рівняння сфери, площини і прямої 79. (x – 1)2 + у2 + (2 – 4)2 = 25. 80. A(10; 0; 0), В(0; 10; 0), С(0; 0; 10). 81. M(3; 2; -1) не належить сфері. X2+ у2 + z2 – 2х + 4у – 6z – 2 = 0, бо 32 + 22 + (-1)2 – 2 × 3 + 4 […]...
- Метод координат. Рівняння сфери, площини, прямої Завдання 2 1. 1) Рівняння сфери, усі точки якої рівновіддалені від початку координат на 1 од. має вигляд х2 + у2 + z2= 1. 2) Оскільки центр сфери – початок координат і вона перетинає ось Оz у точці (0; 0; 1), то вона має радіус 1, а значить, її рівняння; х2 + у2 + z2 […]...
- ВІДПОВІДІ ДО ТЕСТІВ ЕКСПРЕС-КОНТРОЛЮ ВІДПОВІДІ ДО ТЕСТІВ ЕКСПРЕС-КОНТРОЛЮ Тест 1. Тригонометричні функції кутів від 0° до 180° Варіант 1. 1. Б. 2. В. 3. Б. 4. 1. 5. 0. Варіант 2. 1. Б. 2. В. 3. В. 4. . 5. 0. Тест 2. Теорема косинусів та її наслідки Варіант 1. 1. В. 2. Б. 3. А. 4. 5 см. […]...
- Запитання і вправи для повторення § 7 Відповідь: (3; 3), (-1; -2), (1; 0,5). 1012. а) х – 2y = 4; X 0 4 Y -2 0 Б) 4х + у = -4; X 0 -1 Y -4 0 В) 3х – 2y = 6. X 0 2 У -3 0 Відповідь: пара чисел (-2; 3) не являється розв’язком системи рівнянь Х […]...
- Геометричні тіла 628. А) спільна вершина; Б) спільне ребро; В) спільна грань; Г) спільна діагональ. 629. А) дві кулі не мають спільних точок; Б) дві кулі мають одну спільну точку; В) дві кулі, які перетинаються; Г) кулі мають різні радіуси і спільний центр. 630. Дано точку О і r > 0, г – відстань. ОХ ≤ r. […]...
- Властивості сфери і кулі 1. Відстань, яка б відділяла мене від мого антипода дорівнювала б Двом радіусам Землі. Відповідь: 2R Землі. 2. Нехай АО – радіус Землі, ОА = 6400 км, О1А – радіус Полярного кола Землі. Координати Полярного кола Землі 66°31′ п. ш. ∠АОВ = 66°31′; ∠О1ОА = 90° – 67° = 23°. З ΔO1ОA: Ο1Α = ОА […]...
- Розв’язання задач за допомогою систем рівнянь 973. Нехай 1 кг помідорів коштує x грн, а 1 кг огірків – у грн. Складаємо систему рівнянь: Відповідь: 3 грн.; 2 грн. 974. Нехай 1 альбом коштує x грн., а 1 зошит у грн. Складаємо систему рівнянь: Відповідь: альбом коштує 4 грн., зошит – 1 грн. 975. Нехай маса 1 ящика слив x кг, […]...
- Перетворення простору 1. 1) Вектор паралельного перенесення, що переводить відрізок ОА в СВ: Вектор, що переводить відрізок ОС в АВ: 2) Вектор, що переводить ОС в АВ: Вектор, що переводить О А в СВ: 3) Вектор, що переводить ОС в АВ: Вектор, що переводить ОА в СВ: 4) Вектор, що переводить ОС в АВ: Вектор, що переводить […]...
- Відстань між двома точками із заданими координатами УРОК № 24 Тема. Відстань між двома точками із заданими координатами Мета уроку: виведення формули для знаходження відстані між двома точками, заданими координатами, і застосування формул до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і доводять формулу для знаходження відстані […]...
- Рівняння кола УРОК № 26 Тема. Рівняння кола Мета уроку: виведення рівняння кола. Формування вмінь учнів використовувати рівняння кола до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють рівняння кола. Розпізнають рівняння кола. Хід уроку I. Перевірка домашнього завдання Перевірити наявність […]...
- Координати середини відрізка УРОК № 23 Тема. Координати середини відрізка Мета уроку: виведення формул для знаходження координат середини відрізка та формування вмінь учнів застосовувати ці формули до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують та доводять формули координат середини відрізка. Застосовують вивчені формули […]...
- Тематичне оцінювання № 5 Урок 52 Тема. Тематичне оцінювання № 5 Мета уроку: перевірити навчальні досягнення учнів з теми “Декартові координати у просторі”. Хід уроку Тематичне оцінювання № 5 можна провести у вигляді тематичної контрольної роботи. 1. Тематична контрольна робота № 5 Варіант А 1. Чи лежать точки А, В, С на одній прямій, якщо А(1;1;-3), В (-1;3;5), С […]...
- Координатна площина Урок № 113 Тема. Координатна площина Мета: відпрацювати навички “читати” готові рисунки з точкам на координатній площині та будувати точки із заданими координатами; здійснити діагностику знань і вмінь з теми. Тип уроку: застосування знань, умінь, навичок. Хід уроку I. Організаційний момент II. Перевірка домашнього завдання @ Бажано звернути увагу на задачу 4 – повторити спосіб […]...
- Віднімання векторів УРОК № 45 Тема. Віднімання векторів Мета уроку: формування вмінь віднімати вектори, вивчення властивостей різниці векторів; формування вмінь застосовувати вивчені означення та властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині”[13]. Вимоги до рівня підготовки учнів: описують віднімання векторів; відкладають вектор, що дорівнює різниці векторів; формулюють властивості […]...
- Тематичне оцінювання № 6 Урок 61 Тема. Тематичне оцінювання № 6 Мета уроку: перевірка навчальних досягнень учнів з теми “Кути та вектори у просторі”. Тематичне оцінювання № 6 можна провести шляхом виконання тематичної контрольної роботи. І. Тематична контрольна робота № 6 Варіант А 1. Сторона квадрата ОАВС дорівнює 5 (рис. 303). Запишіть координати вектора . (3 бали) 2. Із […]...
- Додавання векторів – Елементи векторної алгебри 3. Елементи векторної алгебри Векторні величини (вектори) – це величини, які характеризуються числовими значеннями і напрямом: Скалярні величини (скаляри) – це величини, які характеризуються лише числовим значенням. Вони можуть бути додатними та від’ємними й додаються алгебраїчно. 3.1. Додавання векторів Якщо вектори спрямовані вздовж однієї прямої або якщо вони паралельні, то результуючий вектор дорівнює алгебраїчній сумі […]...
- Розв’язування задач і вправ. Самостійна робота № 2 Урок № 20. Тема. Розв’язування задач і вправ. Самостійна робота № 2 Мета. Поглиблювати уміння та навички учнів користуватися поняттями відрізка, ламаної, прямої координатного променя та шкал, а також вимірювати величину кутів. Розвивати кмітливість, інтерес до геометрії, виховувати почуття відповідальності. Хід уроку I. Організація класу II. Перевірка домашнього завдання 1. Два учні працюють біля дошки. […]...
- Паралельне перенесення в просторі Урок 49 Тема. Паралельне перенесення в просторі Мета уроку: формування знань учнів про паралельне перенесення в просторі; вивчення його властивостей та застосування їх до розв’язування задач. Обладнання: схеми “Відстань між двома точками” (див. урок 46) і “Координати середини відрізка” (див. урок 47), моделі куба і прямокутного паралелепіпеда. Хід уроку І. Перевірка домашнього завдання 1. Перевірити […]...
- КООРДИНАТНА ПЛОЩИНА Розділ 5 ВИРАЗИ І РІВНЯННЯ § 34. КООРДИНАТНА ПЛОЩИНА Ви вже знаєте, що таке координатна пряма (мал. 162). На ній точка О – початок відліку, стрілка показує напрямок зростання чисел, а ціна поділки становить одну одиницю. Мал. 162 Проте на практиці часто доводиться користуватися орієнтирами не тільки вздовж прямої, а й на площині. Ви знаєте, […]...
- Взаємне розміщення двох кіл Розділ 4. Коло і круг. Геометричні побудови § 25. Взаємне розміщення двох кіл 656. На рис. 404 кола перетинаються. На рис. 405 кола дотикаються. На рис. 406 кола не мають спільних точок. 657. 1) Кола мають внутрішній дотик. 2) Кола перетинаються. 3) Кола концентричні. 658. 1) Кола мають зовнішній дотик. 2) Кола не перетинаються. 659. […]...
- Рівняння прямої УРОК № 28 Тема. Рівняння прямої Мета уроку: виведення рівняння прямої. Формування вмінь учнів використовувати рівняння прямої до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють рівняння прямої. Розпізнають рівняння прямої. Хід уроку I. Перевірка домашнього завдання Перевірити наявність […]...