Розв’язування задач на знаходження кутів у просторі
Урок 57
Тема. Розв’язування задач на знаходження кутів у просторі
Мета уроку: формування вмінь учнів знаходити кути у просторі.
Обладнання: стереометричний набір, модель куба.
Хід уроку
1. Два учні відтворюють розв’язування задач № 48 (2) 49 (1) на дошці.
2. Фронтальне опитування.
1) Сформулюйте теорему про площу ортогональної проекції многокутника.
2) Знайдіть площу ортогональної проекції квадрата з діагоналлю 4 см, якщо кут між площиною квадрата і його проекцією дорівнює: а) 60°; б) 45°.
3) Ребро куба ABCDA1B1C1D1 дорівнює
А) кут між прямою C1D і площиною АВС дорівнює 30°;
Б) кут між прямою B1D і площиною АВС дорівнює 45°;
В) площина АСВ1 утворює з площиною АВС кут, тангенс якого дорівнює 
;
Г) площа перерізу куба площиною, яка проходить через ребро АВ і утворює з площиною АВС кут 30° , дорівнює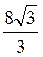 
см2.
3. Перевірка правильності розв’язання задач № 48 (2), 49 (1), що відтворили учні на дошці.
4. Самостійна робота.
1) Кут між площинами? і? дорівнює 60°. Точка А, яка лежить у площині?, віддалена від площини? на 12
2) Через центр О квадрата ABCD проведено до його площини перпендикуляр SO. Кут між прямою SC і площиною квадрата дорівнює 60°. АВ = 18 см. Знайдіть кут між площинами ASC і DSC. (8 балів)
1) Кут між площинами? і? дорівнює 60°. Точка А, яка лежить у площині?, віддалена від площини? на 12 см. Знайдіть відстань від проекції точки А на площину? до лінії перетину площин. (4 бали)
2) Через вершину D тупого кута ромба ABCD проведено до його площини перпендикуляр DM довжиною 9,6 см. Діагоналі ромба дорівнюють 12 і 16 см. Знайдіть кут між площинами АВС і МВС. (8 балів)
1) Кут між площинами? і? дорівнює 30°. Точка А, яка лежить у площині?, віддалена від лінії перетину площин на 12 см. Знайдіть відстань від точки А до площини?. (4 бали)
2) Через центр О квадрата ABCD проведено до його площини перпендикуляр SO. Кут між прямою SC і площиною квадрата дорівнює 60°, АВ = 18 см. Знайдіть кут між площинами АВС і BSC. (8 балів)
1) Кут між площинами? і? дорівнює 30°. Точка А, яка лежить у площині?, віддалена від лінії перетину площин на 12 см. Знайдіть відстань від проекції точки А на площину? до лінії перетину площин. (4 бали)
2) Через вершину D тупого кута ромба ABCD проведено до його площини перпендикуляр DM. Діагоналі ромба дорівнюють 12 і 16 см. Знайдіть кут між площинами AMD і CDM. (8 балів)
Відповідь. Варіант 1. 1) 8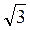
см. 2) arctg 
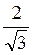. Варіант 2. 1) 4 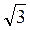см. 2) 45°. Варіант 3. 1) 6 см. 2) arctg 
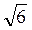. Варіант 4.1) 6 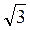см. 2) n – arccos 
.
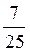Формування вмінь учнів знаходити куги між прямою і площиною, між площинами
1. Кут між прямою а і площиною? дорівнює 45°. Через точку їх перетину в площині? проведено пряму b. Кут між прямими а і b дорівнює 60°. Доведіть, що кут між прямою b і проекцією прямої а на площину? дорівнює 45°.
2. Через сторону AC рівностороннього трикутника АВС проведено площину?. Кут між висотою BD трикутника і цією площиною дорівнює?. Знайдіть кут між прямою АВ та площиною?. (Відповідь, arcsin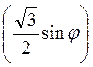 
)
3. Через центр О правильного трикутника АВС проведено до його площини перпендикуляр МО. АВ = а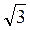. Кут між прямою МА і площиною трикутника дорівнює 45°. Знайдіть кут між площинами: 1) АМО і ВМО; 2) ВМС і АВС.
(Відповідь. 1) 60°; 2) arctg 2)
4. Площини рівносторонніх трикутників АВС і ABD перпендикулярні. Знайдіть кут: 1) між прямою DC і площиною АВС; 2) між площинами ADC і BDC.
(Відповідь. 1) 45°; 2) arccos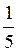
)
Повторити розділ “Вектори” із планіметрії та розв’язати задачу № 63 (с. 59).
IV. Підведення підсумку уроку
Запитання до класу
1) Дайте означення кута між мимобіжними прямими.
2) Дайте означення кута між прямою і площиною.
3) Дайте означення кута між площинами.
(1 votes, average: 5.00 out of 5)
Loading...