РОЗВ’ЯЗУВАННЯ ЗАДАЧ ЗА ДОПОМОГОЮ СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ
Цілі:
– навчальна: сформувати вміння складати системи рівнянь за умовою задачі; домогтися засвоєння схеми розв’язання задачі за допомогою системи лінійних рівнянь з двома змінними;
– розвивальна: сприяти розвитку логічного мислення, уваги учнів; формувати вміння грамотно формулювати власні думки;
– виховна: виховувати позитивне ставлення до навчання, старанність, спостережливість;
Тип уроку : засвоєння нових знань, умінь, навичок.
Обладнання та наочність:
Хід уроку
І. ОРГАНІЗАЦІЙНИЙ ЕТАП
______________________________________________________
______________________________________________________
______________________________________________________
ІІ.
1. Перевірка завдання, заданого за підручником
______________________________________________________
______________________________________________________
2. Самостійна робота з подальшою взаємоперевіркою
Варіант 1 | Варіант 2 |
1) При якому значенні х набувають рівних значень вирази | |
26 – 4х і 12х – 7(х + 4)? | 3х – 9(х – 5) і -11 + 2х? |
2) Розв’яжіть задачу | |
Відстань між пунктами А і B дорівнює 40 км. Із пункту B виїхав велосипедист, а з пункту | З пунктів А і B виїхали назустріч один одному відповідно автомобіль і велосипедист. Велосипедист проїхав до зустрічі відстань, у 3 рази меншу, ніж автомобіль. На якій відстані від А вони зустрілися, якщо від А до B дорівнює 80 км? |
ІІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ
Математичний диктант
Варіант 1 | Варіант 2 |
Опишіть за допомогою рівняння ситуацію: | |
1) сума чисел х і у дорівнює 20; 2) число х удвічі більше за число у; 3) середнє арифметичне чисел х і у дорівнює 17; 4) периметр квадрата зі стороною х на 5 більший за периметр квадрата зі стороною у; 5) за 3 пиріжки вартістю х грн кожний і 1 булочку вартістю у грн заплатили 9,5 грн | 1) різниця чисел х і у дорівнює 30; 2) число х утричі менше від числа у; 3) подвоєна сума чисел х і у дорівнює 16; 4) олівець вартістю х грн дешевший, ніж ручка вартістю у грн, на 0,1 грн; 5) груша масою х г і 5 яблук масою у г кожне мають загальну масу 900 г |
ІV. ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ
План вивчення теми
1. Приклад задачі, яку зручно розв’язувати за допомогою системи рівнянь.
2. Алгоритм розв’язування задачі складанням системи рівнянь:
1) позначити невідомі величини буквами;
2) за умовою задачі скласти два рівняння;
3) записати й розв’язати систему цих рівнянь;
4) перевірити, чи задовольняє розв’язок системи рівнянь умову задачі;
5) дати відповіді на запитання, поставлені в задачі.
V. ЗАСВОЄННЯ НОВИХ ЗНАНЬ І ВМІНЬ
1. Робота за підручником
______________________________________________________
______________________________________________________
2. Додаткові завдання
1) Знайдіть два числа, якщо середнє арифметичне цих чисел дорівнює 36, а 0,2 їхньої різниці дорівнює 0,8.
2) Дві гирі й три гантелі важать а кг, а три гирі важчі, ніж шість гантелей, на b кг. Скільки важать окремо одна гиря й одна гантеля? Чи відповідають змісту задачі а = 16, b = 3? а = 10, b = 2?
VІ. ПІДСУМКИ УРОКУ
1.
______________________________________________________
______________________________________________________
2. Виконання усних вправ
1) Під час розв’язування задачі було зроблено позначення: x – кількість автівок на стоянці; у – кількість вантажівок. Чи може бути розв’язком задачі пара чисел:
А) (25; -15); б) (31,5; 29,5); в) (19; 16); г) (7; 3 276 069)?
2) Складіть систему рівнянь, яка відповідає умові:
А) Сума двох чисел дорівнює 80, а їх різниця дорівнює 15.
Б) У класі 36 учнів. Дівчат на 4 менше, ніж хлопців.
В) Два токарі виготовили 172 деталі, перший працював 3 години, а другий – 2 години. Якби перший працював 1 годину, а другий – 4 години, то вони виготовили б 198 деталей.
3) Придумайте ситуацію, яку можна описати за допомогою системи рівнянь:
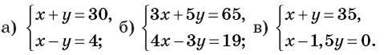
VII. ДОМАШНЄ ЗАВДАННЯ
1. Завдання за підручником:
______________________________________________________
______________________________________________________
2. Додаткове завдання. Сума 5 % одного числа і 4 % другого числа дорівнює 46, а сума 4 % першого числа і 5 % другого числа дорівнює 44. Знайдіть ці числа.
Відповідь. 600 і 400.
