РУХОМИЙ І НЕРУХОМИЙ БЛОКИ
РОЗДІЛ 4 МЕХАНІЧНА РОБОТА ТА ЕНЕРГІЯ
& 35. РУХОМИЙ І НЕРУХОМИЙ БЛОКИ
Перший блок було винайдено, коли через колесо, що обертається навколо осі, невідомий механік давнини перекинув мотузку і за допомогою цього пристрою почав підіймати вантажі. За легендою, Архімед за допомогою декількох блоків зміг спустити на воду важке судно, яке не могли зрушити з місця десятки коней. Зараз блоки є в багатьох машинах і механізмах. Чим пояснюється їх широке застосування?
1. З’ясовуємо зв’язок нерухомого блока
На рис. 35.1, а зображене колесо (1) із жолобом (2). Вісь колеса (3) закріплена нерухомо в обоймі (4); колесо має можливість обертатися навколо цієї осі. Через жолоб перекинуто мотузку (5). Перед нами простий механізм – нерухомий блок.
Блок – це простий механізм, що має форму колеса із жолобом по ободу, через який перекинуто мотузку (канат).
Важіль і нерухомий блок, на перший погляд, є зовсім різними механізмами. Насправді нерухомий блок – це важіль з однаковими плечима. Дійсно, прикладемо до кінців мотузки, перекинутої через блок, сили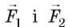 
й опустимо перпендикуляри з точки опори
З умови рівноваги важеля (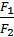
= 
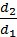) випливає, що = 
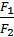= 1.
Або:
F1 = F2
Отже, нерухомий блок не дає виграшу в силі, проте дозволяє змінювати напрямок дії сили (див., наприклад, рис. 35.1-35.3).
Розгляньте рис. 35.1, б, в. Якщо вільний кінець мотузки потягти вниз, куди рухатиметься вантаж? куди рухатиметься візок?
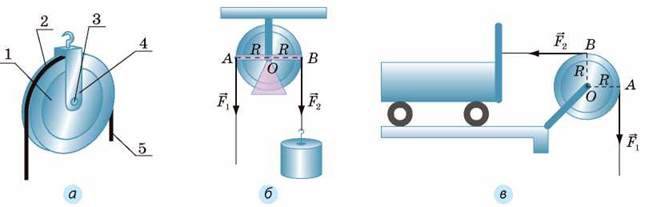
Рис. 35.1. Нерухомий блок можна розглядати як важіль з однаковими плечима. На схемах (б, в): R – радіус блока; О – точка опори; OА – плече сили F; OВ – плече сили F2.
2. Досліджуємо рухомий блок
За допомогою спеціальної обойми причепимо вантаж до осі блока. Сам блок підвісимо на мотузку, один кінець якої закріпимо (рис. 35.4). Якщо піднімати вільний кінець мотузки, то за мотузкою підніматиметься і блок разом із вантажем. Отриманий простий механізм – це рухомий блок.
Рухомий блок можна розглядати як важіль, що обертається навколо осі, яка проходить через точку опори O (див. рис. 35.4). З рисунка бачимо, що плече сили F2 дорівнює радіусу блока (відрізок OA), а плече сили F1 – діаметру блока (відрізок ОБ), тобто двом його радіусам.
Скориставшись умовою рівноваги важеля (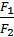 = 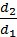) і врахувавши, що d1 = 2R, d2 = R, отримаємо:
= 
= 
.
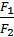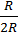Або:
F1 =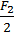 
.
Рис. 35.2. Нерухомі блоки, які є в конструкції кар’єрних екскаваторів, дозволяють змінювати напрямок дії сил під будь-яким кутом
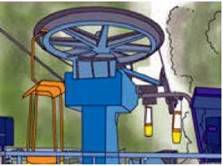
Рис. 35.3. Нерухомий блок у механізмі канатної дороги змінює напрямок дії сили натягу каната (а отже, напрямок руху каната) на протилежний
Отже, використання рухомого блока дає змогу отримати виграш у силі в 2 рази.
Зрозуміло, що виграш у силі буде супроводжуватися таким самим програшем у відстані: якщо вільний кінець мотузки підняти на висоту h, то блок разом із вантажем піднімуться лише на висоту – (рис. 35.5).
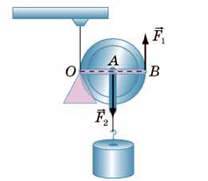
Рис. 35.4. Рухомий блок можна розглядати як важіль з відношенням плечей 1 : 2. На схемі: О – точка опори; OА – плече
Cили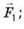 
OВ – плече сили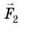 
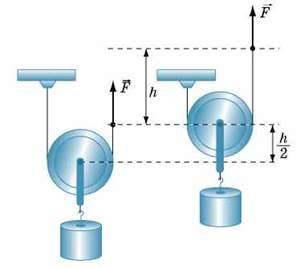
Рис. 35.5. Щоб підняти вантаж на висоту 
, вільний кінець мотузки слід підняти на висоту h
Як і важіль, рухомий блок можна використовувати й для отримання виграшу у відстані (або виграшу у швидкості руху). Для цього вантаж слід причепити до вільного кінця мотузки, а тягти за обойму, до якої прикріплена вісь блока (рис. 35.6).
Нерухомі та рухомі блоки, як правило, використовують одночасно – у вигляді системи блоків (рис. 35.7).
Як ви вважаєте, чи дозволяє зображена на рис. рис. 35.7 система блоків змінити напрямок дії сили? отримати виграш у силі?
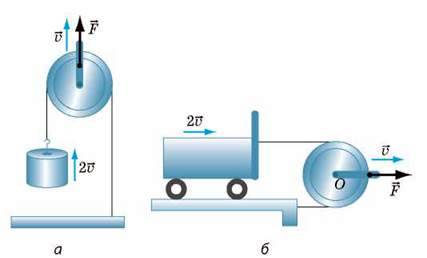
Рис. 35.6. Якщо точку прикладання сили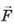 
переміщувати з певною швидкістю v, то вантаж (а) і візок (б) рухатимуться вдвічі швидше
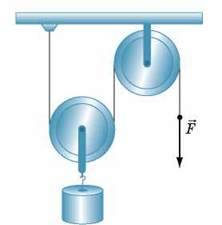
Рис. 35.7. Для підняття вантажів незамінними є комбінації нерухомого та рухомого блоків
3. Учимося розв’язувати задачі
Задача. На рис. 35.8 зображено систему блоків.
Якими є сили натягу мотузок а і b, якщо маса вантажу дорівнює 20 кг?
Який виграш у силі дає ця система блоків?
На яку відстань hA опуститься точка A, якщо вантаж підніметься на висоту 10 см?
Масою блоків і силою тертя знехтуйте.
Аналіз фізичної проблеми. Система блоків складається з двох рухомих блоків (1 і 2) та одного нерухомого блока (3). За умовою блоки невагомі, отже, натяг мотузок спричиняється лише вагою вантажу. Для визначення виграшу в силі порівняємо вагу P вантажу та силу F, яка прикладена до вільного кінця мотузки і під дією якої піднімається вантаж.
Слід урахувати, що, вигравши в силі, ми в стільки ж разів програємо у відстані, на яку переміщується вантаж.
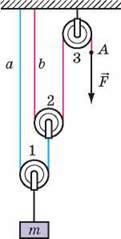
Рис. 35.8. До задачі в & 35
Дано:
M = 20 кг
H = 10 см
G = 10 
Знайти:
Fa – ?
Fb – ?
– ?
HA – ?
Пошук математичної моделі, розв’язання.
Знайдемо вагу вантажу: P = mg = 20 кг 10 = 200 Н.
Рухомий блок 1, до обойми якого підвішено вантаж, дає виграш у силі в 2 рази, отже, сила натягу мотузки, a у 2 рази менша за вагу вантажу:
Fa =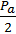 
= 
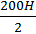= 100 H.
Рухомий блок 2, до обойми якого підвішено мотузку a, також дає виграш у силі в 2 рази, отже, сила натягу мотузки b становить:
Fb =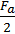 
= 
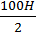= 50 H.
Сила F є силою натягу мотузки b: F = Fb = 50 Н.
Тому виграш у силі становить:
= 
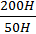= 4.
У скільки разів ми виграли в силі, у стільки ж разів програли у відстані: hA = 4h = 40 см.
Аналіз результату: у системі два рухомі блоки, обидва застосовують для виграшу в силі. Кожний рухомий блок дає виграш у силі в 2 рази, тому загальний виграш у силі дорівнює 4. Отже, ми отримали реальний результат.
Відповідь: Fa = 100 Н; Fb = 50 Н; виграш у силі – 4; hA = 40 см.
Підбиваємо підсумки
Блок – це простий механізм, що має форму колеса із жолобом по ободу, через який перекинуто мотузку (канат). Розрізняють рухомий і нерухомий блоки.
Нерухомий блок подібний до важеля з однаковими плечима, і тому він не дає виграшу в силі, проте дозволяє змінювати напрямок дії сили.
Рухомий блок подібний до важеля, в якого відношення плечей становить 1 : 2, і тому він дає виграш у силі в 2 рази. Але це супроводжується програшем у відстані в 2 рази. Рухомий блок також застосовують і для отримання виграшу у відстані (виграшу у швидкості руху).
Для більшої ефективності зазвичай використовують комбінації рухомого та нерухомого блоків.
Контрольні запитання
1. Опишіть нерухомий блок. 2. Чому нерухомий блок не дає виграшу в силі? 3. Для чого використовують нерухомий блок? 4. Опишіть рухомий блок. 5. Який виграш у силі дає рухомий блок? 6. Що означає вираз: “Рухомий блок дає програш у відстані в 2 рази”? 7. Як за допомогою блоків отримати виграш у силі більш ніж у 2 рази?
Вправа № 35
У завданнях 1-3 масою блоків і дією сили тертя знехтуйте.
1. Розгляньте рис. 1 і дайте відповіді на запитання: а) який блок зображений на рисунку? б) на скільки підніметься вантаж, якщо вільний кінець мотузки витягти вгору на 10 см? в) з якою силою тягнуть мотузку, якщо вага вантажу 60 Н?
2. Вільний кінець мотузки тягнуть із силою F = 40 Н (рис. 2). Якою є маса вантажу? На скільки підніметься вантаж, якщо витягти мотузку на 24 см?
3. Вантаж піднімають за допомогою одного нерухомого і двох рухомих блоків (див. рис. 35.8). Якою є маса вантажу і на скільки він підніметься, якщо під дією сили 75 Н вільний кінець мотузки опустити на 60 см?
4. Яку силу F треба прикласти до вільного кінця мотузки (див. рис. 2), щоб підняти вантаж масою 100 кг, якщо маса рухомого блока становить 2 кг? Вважайте, що тертя в осях відсутнє.
5. Вантаж масою m утримується за допомогою системи блоків (рис. 3). Визначте силу натягу кожної мотузки. Тіла системи вважайте невагомими.
6. У системі на рис. 4 маса вантажу 3 дорівнює 1 кг, маса кожного блока – 100 г. Система зрівноважена та нерухома. Знайдіть маси вантажів 1 і 2. Масою мотузки і тертям у блоках знехтуйте.
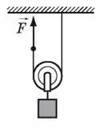
Рис. 1
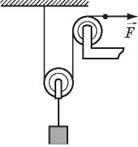
Рис. 2
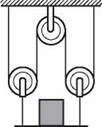
Рис. 3
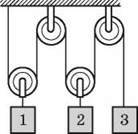
Рис. 4
7. У техніці досить часто використовують поліспасти – пристрої, які складаються із системи рухомих і нерухомих блоків. На рис. 5 подано схематичне зображення одного з поліспастів – лебідки. Скористайтесь додатковими джерелами інформації і дізнайтеся про поліспасти більше. Підготуйте повідомлення.
8. Окрім блоків різновидом важеля є коловорот (див., наприклад, рис. 6). Скористайтесь додатковими джерелами інформації і дізнайтеся, що являє собою коловорот, де його застосовують, завдяки чому за допомогою коловорота можна отримати значний виграш у силі. Підготуйте повідомлення.
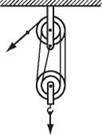
Рис. 5
Рис. 6
Відеодослід. Перегляньте відеоролик і поясніть спостережуване явище.
(1 votes, average: 5.00 out of 5)
Loading...