Симетрія відносно прямої
УРОК № 35
Тема. Симетрія відносно прямої
Мета уроку: формування поняття симетрії відносно прямої; вивчення властивостей симетрії відносно прямої; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач.
Тип уроку: комбінований.
Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13].
Вимоги до рівня підготовки учнів: описують симетрію відносно прямої; будує фігури, у які переходять дані фігури при симетрії відносно прямої; наводять приклади фігур, які мають вісь симетрії; застосовують
Хід уроку
І. Перевірка домашнього завдання
1. Перевірити наявність виконаних домашніх завдань та відповісти на запитання, які виникли в учнів при їх виконанні. 2. Фронтальна бесіда 1) Дайте означення симетрії відносно точки. 2) Які фігури називаються центральносиметричними? Наведіть приклади. 3) Укажіть координати точки, яка симетрична точці A(a; b) відносно початку координат.
ІІ. Поетапне сприймання й усвідомлення нового матеріалу
Поняття симетрії відносно прямої
Точки X і X1 називаються симетричними відносно прямої l, якщо пряма
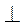 XX1.
XX1.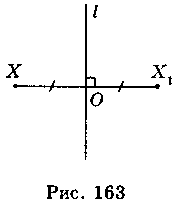
Перетворення фігури F на фігуру F1, при якому кожна точка X фігури F переходить у точку Х1 фігури F1, симетричну їй відносно даної прямої l, називається перетворенням симетрії відносно прямої l або осьовою симетрією (рис. 164). При цьому фігури F і F1 називаються симетричними відносно прямої l, а пряма l – віссю симетрії.
Властивості осьової симетрії
1) Перетворення осьової симетрії є переміщенням. 2) Осьова симетрія перетворює пряму на пряму; відрізок – на відрізок; многокутник – на рівний йому многокутник. 3) Точки, що належать осі симетрії, відображаються самі на себе. 4) Якщо точки М(х; у) і N(x1; y1) симетричні (рис. 165) відносно:
А) осі Ох, то виконується умова 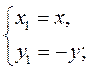
Б) осі Оу, то виконується умова 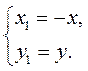
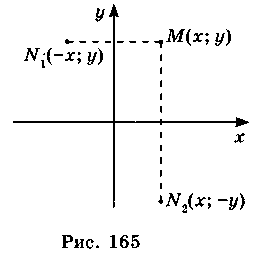
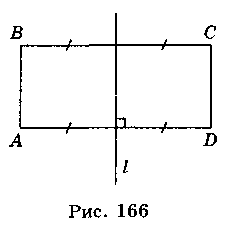
Якщо перетворення симетрії відносно прямої l переводить фігуру F у себе, то ця фігура називається симетричною відносно прямої l, а пряма l – називається віссю симетрії (рис. 166).
Виконання вправ
1. Побудуйте довільний трикутник ABC і симетричний йому трикутник відносно осі:
А) АВ; б) ВС.
2. Скільки осей симетрії має:
А) коло;
Б) прямокутник;
В) квадрат;
Г) ромб;
Д) рівносторонній трикутник?
ІІІ. Закріплення й осмислення нового матеріалу
Розв’язування задач
1. Побудуйте довільний трикутник і трикутник, симетричний даному, відносно прямої, якщо вона:
А) розміщена поза трикутником;
Б) має лише одну спільну точку з трикутником;
В) перетинає дві сторони трикутника.
2. Чотирикутник ABCD заданий координатами своїх вершин: А(1; 1); В(-3; 2), С(-1; -2), D(5; -3). Знайдіть координати вершин чотирикутника, який симетричний даному відносно осі:
А) Ох; б) Оу.
3. Доведіть властивості симетрії відносно прямої. 4. Запишіть рівняння кола, яке симетричне колу (х – 1)2 + (у + 2)2 = 1 відносно:
А) осі Ох; б) осі Оу.
5. Запишіть рівняння прямої, яка симетрична прямій х + у = 1 відносно:
А) осі Ох; б) осі Оу.
6. Дано пряму MN і точки А і В в різних півплощинах відносно MN і на різній відстані від неї. Через точки А і В проведіть прямі так, щоб кут між ними ділився прямою MN навпіл.
IV. Домашнє завдання
1. Вивчити теоретичний матеріал. 2. Розв’язати задачі. 1) Запишіть рівняння кола, яке симетричне колу (х + 1)2 + (у + 1)2 = 1 відносно:
А) осі Ох; б) осі Оу.
2) Запишіть рівняння прямої, яка симетрична прямій х – у = 1 відносно:
А) осі Ох; б) осі Оу.
V. Підбиття підсумків уроку
Запитання до класу
1. Які точки називаються симетричними відносно прямої? 2. Яке перетворення називається симетрією відносно даної прямої? 3. Яка фігура називається симетричною відносно даної прямої? 4. Що таке вісь симетрії? Наведіть приклади.
