Степінь натурального числа з натуральним показником
Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ
§ 7. Степінь натурального числа з натуральним показником
Уже відомо, що суму, в якій всі доданки рівні між собою, можна записати коротше – у вигляді добутку. Наприклад,
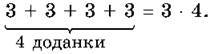
У математиці є спеціальний спосіб і для запису добутку, в якому всі множники рівні між собою. Наприклад,
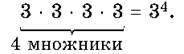
Вираз 34 називають степенем і читають так: “три у четвертому степені”.
У виразі 34 число 3 називають основою степеня, а число
Приклади:
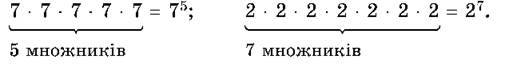
У степеня 75 основа степеня дорівнює 7, а показник 5; у степеня 27 основа степеня дорівнює 2, а показник 7.
Другий степінь числа називають ще квадратом числа. Так, наприклад, запис 92 читають так: “дев’ять у квадраті” (або “дев’ять у другому степені”).
Третій степінь числа називають ще кубом числа. Так, наприклад, запис 43 читають: “чотири у кубі” (або “чотири
Обчислення степеня числа ще називають піднесенням до степеня.
Приклади:
1) 172 = 17 ∙ 17 = 289;
2) 53 = 5 ∙ 5 ∙ 5 = 125;
3) 28 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 = 256.
Приклад 1. Піднеси до квадрата і куба перші десять натуральних чисел.
Розв’язання. Результати можна записати у вигляді таблиці.
N | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
N2 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 |
N3 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 | 1000 |
У математиці не можна знайти добуток, що складається з одного множника. Тому домовилися, що степінь з показником 1 дорівнює основі степеня. Наприклад, 31 = 3; 20131 = 2013, і взагалі а1 = а.
Піднесення до степеня – це нова, п’ята арифметична дія. Черговість її виконання при знаходженні значення числового виразу визначається таким правилом.
Якщо в числовий вираз входить степінь, то спочатку виконується піднесення до степеня, а після цього інші дії.
Приклад 2. Знайди значення виразу: 1) 6 ∙ 32; 2) 5 + 24.
Розв’язання.
1) 6 ∙ 32 = 6 ∙ 9 = 54;
2) 5 + 24 = 5 + 16 = 21.
Початковий рівень
255. Подай у вигляді степеня добуток:
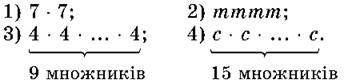
256. Подай у вигляді степеня добуток: 1) 15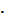 
15 ∙ 15; 2) р ∙ р ∙ р ∙ р ∙ р;
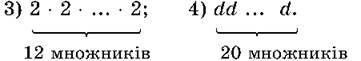
257. Подай у вигляді добутку степінь:
1) 20132; 2) b3; 3) а5; 4) 710.
258. Подай у вигляді добутку степінь:
1) t2; 2) 43; 3) 74; 4) d6.
259. Назви основу і показник степеня:
1) 413; 2) а8; 3) р2;
4) 71; 5) d3; 6) 1817.
Середній рівень
260. Знайди значення степеня:
1) 32; 2) 43; 3) 171;
4) 07; 5) 14; 6) 25.
261. Знайди значення степеня:
1) 72; 2) 141; 3) 23;
4) 15; 5) 09; 6) 34.
262. Склади таблицю квадратів чисел від 11 до 20.
263. Обчисли:
1) 272; 2) 1002; 3) 113;
4) 133; 5) 802; 6) 203.
264. Обчисли:
1) 52 + 1; 2) 73 – 10; 3) 20 – 32.
265. Обчисли:
1) 362; 2) 153; 3) 702;
4) 133 – 1; 5) 422 + 17; 6) 37 – 62.
266. Піднеси до квадрата числа: 1) 16; 2) 37.
267. Піднеси до квадрата числа: 1) 14; 2) 29.
268. Піднеси до куба числа: 1) 5; 2) 12.
269. Піднеси до куба числа: 1) 6; 2) 15.
Достатній рівень
270. Знайди значення виразу:
1) х2 – 8, якщо х = 3, 9, 21;
2) 5у3 + 1, якщо у = 2, 3, 7.
271. Знайди значення виразу:
1) 2a2 – 3, якщо a = 5, 10, 15;
2) b3 + 12, якщо b = 7, 10, 12.
272. Знайди значення виразу:
1) 202 : 5 – 33; 2) (15 – 32)3;
3) (93 – 53) : (9 – 5); 4) (73 – 63)2.
273. Знайди значення виразу:
1) 182 : 9 + 122 : 3; 2) (72 – 62) : (17 – 42);
3) 43 : 8 + 23; 4) (152 – 122) : (15 – 12).
274. Використовуючи таблиці квадратів і кубів чисел, знайди n, якщо:
1) n2 = 121; 2) 225 = n2; 3) n3 = 125; 4) 343 = n3.
275. Використовуючи таблиці квадратів і кубів чисел, знайди m, якщо:
1) m2 = 196; 2) 216 = m3.
Високий рівень
276. На скільки квадрат суми чисел 7 і 9 більший за суму їх квадратів?
277. На скільки куб суми чисел 4 і 5 більший за суму їх кубів?
278. Перевір, які з рівностей правильні:
1) 62 + 82 = 102; 2) 32 + 42 = 72;
3) 112 = 92 + 22 + 62; 4) 23 + 33 = 43.
279. Перевір, які з рівностей правильні:
1) 42 + 52 = 72; 2) 82 + 152 = 172;
3) 22 + 32 + 62 = 72; 4) 53 = 43 + 33.
280. Запиши у вигляді степеня з основою 3 число:
1) 3; 2) 9; 3) 81; 4) 243.
281. Запиши у вигляді степеня з основою 2 число:
1) 2; 2) 8; 3) 16; 4) 64.
282. Якою цифрою закінчується число:
1) 20052;
2) 1 092 0043;
3) 8792 – 2003;
4) 40912 + 80223?
Ф Вправи для повторення
283. Порівняй значення виразів 5a + 15 та а + 59, якщо a = 13.
284. На складі було 32 великих і 48 малих ящиків з товаром. У кожному великому ящику було по а кілограмів товару, а в малому – по b кілограмів. Весь товар вивезли на двох машинах, завантаживши їх однаково. Склади буквений вираз для обчислення маси товару на одній машині та обчисли його значення, якщо а = 16, b = 12.
(1 votes, average: 5.00 out of 5)
Loading...