СУМА КУТІВ ТРИКУТНИКА
РОЗДІЛ 3 ТРИКУТНИКИ
& 10. СУМА КУТІВ ТРИКУТНИКА
Теорема 8 Сума кутів трикутника дорівняй: 180°.
Доведення. Нехай ABC – довільний трикутник (мал. 130). Через йот вершину С проведемо пряму КР, паралельну стороні АВ.
Утворені кути АСК і ВСР позначимо цифрами 1 і 2. Тоді ∠A = ∠1, ∠B = ∠2, як внутрішні різносторонні кути при паралельних прямих АВ і КР та січних АС і ВС. Кути 1, 2 і С в сумі дорівнюють розгорнутому куту, тобто 180°. Тому
∠A + ∠B + ∠C = ∠1 + ∠2 + ∠C = 180°.
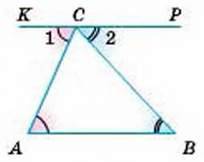
Мал. 130
Отже, ∠А + ∠В + ∠С
Зверніть увагу! У доведеній теоремі 8 йдеться про суму мір кутів трикутника. Але для спрощення формулювань замість “міра кута” часто вживають слово “кут”.
Наслідок Трикутник не може мати двох прямих або двох тупих кутів. У кожному трикутнику принаймні два кути – гострі.
Іноді крім кутів трикутника (внутрішніх) розглядають також його зовнішні кути. Зовнішнім кутом трикутника називають кут, утворений стороною трикутника і продовженням його іншої сторони. Наприклад, зовнішнім кутом трикутника ABC при вершині А є кут КАС (мал. 131).
Теорема 9 Зовнішній кут трикутника дорівнює сумі двох внутрішніх
Доведення. Нехай ∠КАС – зовнішній кут трикутника ABC (див. мал. 131). Тоді
∠КАС = 180° – ∠ВАС (згідно з теоремою про суміжні кути),
∠В + ∠C = 180° – ∠ВАС (згідно з теоремою про суму кутів трикутника).
Отже, ∠КАС = ∠B + ∠С.
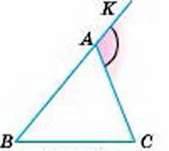
Мал. 131
Наслідок Зовнішній кут трикутника більший за кожний внутрішній кут, не суміжний із ним.
Зверніть увагу! При кожній вершині трикутника можна побудувати два зовнішні кути, продовживши одну чи іншу його сторону. Наприклад, кожний із кутів КАС і РАВ – зовнішній кут трикутника ABC при вершині А (мал.132). Такі два зовнішні кути – вертикальні, тому дорівнюють один одному.
ДЛЯ ДОПИТЛИВИХ
Теорему про суму кутів трикутника можна узагальнити і поширити на довільні многокутники.
Кожний чотирикутник можна розрізати на два трикутники, сполучивши його протилежні вершини відрізком. (Якщо один із кутів чотирикутника більший від розгорнутого, то саме його вершину слід сполучити з протилежною, як на малюнку 133.) Сума всіх кутів чотирикутника дорівнює сумі всіх кутів двох утворених трикутників, тобто 180°. 2. Отже, сума кутів будь-якого чотирикутника дорівнює 360°?.
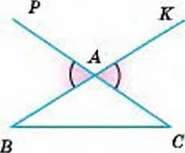
Мал. 132
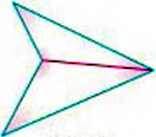
Мал. 133
Довільний п’ятикутник можна розрізати на чотирикутник і трикутник або на 3 трикутники (мал. 134).
Отже, сума кутів п’ятикутника дорівнює 180° ∙ З, тобто 540°.
Спробуйте написати формулу, за якою можна обчислити суму кутів довільного n-кутника.
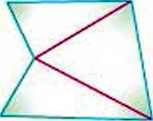
Мал. 134
Запитання і завдання для самоконтролю
1. Сформулюйте та доведіть теорему про суму кутів трикутника.
2. Що таке зовнішній кут трикутника?
3. Сформулюйте та доведіть теорему про зовнішній кут трикутника.
4. Чи правильно, що зовнішній кут трикутника більший за кожний внутрішній кут, не суміжний із ним?
5. Чому дорівнює сума кутів чотирикутника?
Виконаємо разом
1. Чому дорівнює сума зовнішніх кутів трикутника, взятих при кожній вершині по одному?
Нехай ABC – довільний трикутник. Позначимо його зовнішні кути цифрами 1, 2 і 3 (мал. 135).
Перший спосіб:
Згідно з теоремою про зовнішній кут трикутника
∠1 = ∠B + ∠C, ∠2 = ∠A + ∠B, ∠2 = ∠А + ∠C.
Додавши окремо ліві й праві частини цих рівностей, матимемо:
∠1 + ∠2 + ∠3 = 2(∠A + ∠B + ∠C) = 2 ∙ 180° = 360°.
Другий спосіб:
∠1 + ∠2 + ∠3 = 180° – ∠A + 180° – ∠B + 180° – ∠C = 540° – (∠A + ∠B + ∠C) = 640° – 180° = 360°.
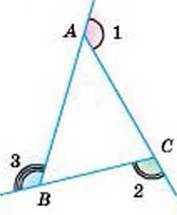
Мал. 135
Отже, сума зовнішніх кутів трикутника, взятих по одному при кожній вершині, дорівнює 360°.
2. Доведіть, що в кожному трикутнику є кут не більший за 60° і кут не менший від 60°.
Якби кожний кут трикутника був менший від 60° то сума всіх йот кутів становила б менше 180°, я це неможливо. Якби кожний кут трикутника був більший за 60°, то сума всіх його кутів була б більшою за 180°, що також неможливо.
Отже, у кожному трикутнику є кут, не більший за 60°, і кут, не менший від 60°.
ЗАДАЧІ І ВПРАВИ
Виконайте усно
289.Сума двох кутів трикутника дорівнює 80°. Знайдіть третій кут.
290. Два кути трикутника дорівнюють по 30°. Знайдіть третій кут.
291. Чи існує трикутник з кутами: 60°, 70° і 80°?
292. Два кути трикутника дорівнюють 20° і 80°. Знайдіть третій кут.
293. Знайдіть кути прямокутного трикутника, якщо один із них дорівнює 30°.
А
294. Знайдіть кути трикутника, якщо вони пропорційні числам:
А)2, 3 і 5; б)1, 5 і 6; в) ,
,  ,
,  .
.
295. Доведіть, що сума гострих кутів прямокутного трикутника дорівнює: 90°.
296. Заповніть порожні клітинки таблиці про кути трикутника ABC.
∠A | 30° | 20° | 83° | 95° | 54° |
∠B | 70° | 45° | 35° | 47° | |
∠C | 100° | 45° | 17° | 67° | 54° |
297. Знайдіть кути трикутника, якщо один із них:
А) дорівнює другому і менший від третього на 30°;
Б) більший за другий на 20°, а за третій – на 40°;
В) більший за другий у 2 рази, а за третій – на 10°.
298. У трикутнику ABC кути А і В дорівнюють по 66°. Знайдіть зовнішній кут трикутника при вершині С.
299. Чи може кожний зовнішній кут трикутника дорівнювати 100°?
300. Кути трикутника пропорційні числам 1, 2 і 3. Доведіть, що цей трикутник прямокутний.
Б
301. Знайдіть кути трикутника ABC, якщо ∠A + ∠B = 100° і ∠B + ∠C = 120°.
302. ∠ABC = 30°. Під яким кутом пряма АС перетинає промінь ВС, якщо промінь ВА вона перетинає під кутом 45°?
303. СН і CL – висота і бісектриса трикутника ABC, ∠A = 60°, ∠B = 30°. Знайдіть ∠HCL.
304. CL – бісектриса трикутника ABC, ∠A = 80°, ∠B = 40°. Знайдіть: a) ∠CLA; б) під яким кутом перетинаються бісектриси кутів А і В.
305. СН – висота трикутника ABC. Знайдіть ∠ACH і ∠BCН, якщо:
А) ∠A = 30° і ∠B = 60°;
Б) ∠A = 30° і ∠B = 120°.
306. Знайдіть міри зовнішніх кутів трикутника ABC, якщо:
А) ∠A = 40°, ∠В = 50°;
Б) ∠B = 120°, ∠C = 40°;
В) ∠A + ∠В = 100°, ∠B + ∠C = 130°;
Г) ∠A + ∠C = 95°, ∠В + ∠С = 135°.
307. Кути А і В трикутника ABC – рівні. Доведіть, що бісектриса зовнішнього кута трикутника ABC при вершині С паралельна стороні АВ.
308. Знайдіть суму кутів А, В, С, D, Е п’ятикутної зірки (мал. 136).
309. Трикутник АВС розташований на поверхні куба, як показано на малюнку 137. Знайдіть суму кутів, позначених на малюнку цифрами.
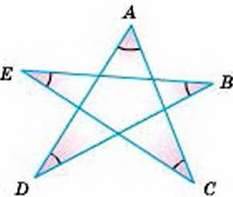
Мал. 136
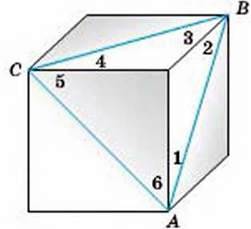
Мал. 137
310. Прямолінійний тунель АВ пробивають із двох боків гори (мал. 138). Чи правильно вибрано напрямки A1A і B1В, якщо вимірювання показали, що ∠A = 50°, 10′, ∠B = 48° 20′ і ∠C = 80° 5′?
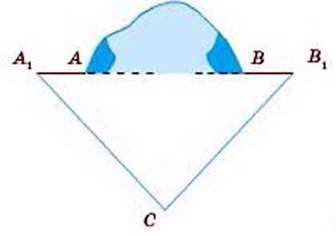
Мал. 138
Практичне завдання
311. Пакресліть довільний трикутник і проведіть усі його бісектриси. Що ви помітили? Чи можна стверджувати, що всі три бісектриси трикутника проходять через одну точку? А всі три медіани трикутника?
ВПРАВИ ДЛЯ ПОВТОРЕННЯ
312. Відрізок, довжина якого дорівнює а, поділенo на два нерівні відрізки. Знайдіть відстань між серединами утворених відрізків.
313. Один із суміжних кутів на 20° більший за інший. У скільки разів перший кут більший за другий?
314. Периметр квадрата дорівнює 4 дм. Чи можна з нього вирізати трикутник” периметр якого дорівнює 3 дм?
315. Чи існує трикутник, периметр якого у 1000 разів більший за одну з його сторін? А за одну з висот?
316. Січна с з паралельними прямими а і b утворює внутрішні односторонні кути, що відносяться як 2 : 3. Як відносяться кути, утворені бісектрисами цих кутів і січною с?
