СУМІЖНІ І ВЕРТИКАЛЬНІ КУТИ
Геометрія Евкліда є лише першим кроком до вивчення форм реального простору.
О. Смогоржевський


РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ
У цьому розділі підручника ви розширите і поглибите свої знання про прямі і промені однієї площини, ознайомитеся з дуже важливими поняттями: суміжні кути, вертикальні кути, перпендикулярні прямі, паралельні прямі тощо, а також із важливими загальноматематичними поняттями: аксіома, теорема, наслідок, доведення, ознака, означення.
& 4. СУМІЖНІ І ВЕРТИКАЛЬНІ КУТИ
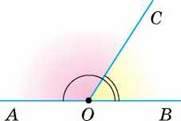
Два кути, на які розбивається розгорнутий кут його внутрішнім променем, називають суміжними.
Одна сторона в суміжних кутів спільна, а дві інші – доповняльні промені. Якщо точки А, О, В лежать на одній прямій, а С – довільна точка, яка не належить прямій АВ, то кути АОС і СОВ – суміжні (мал. 45).
Властивість суміжних кутів сформулюємо у вигляді теореми.
У математиці теоремою називають кожне твердження, істинність якого обгрунтовується за допомогою логічних міркувань. Ланцюжок таких міркувань називають доведенням1.
У нашому підручнику
Мал. 45
Теорема 1 Сума мір двох суміжних кутів дорівнює 180°.
Доведення. Об’єднання двох суміжних кутів є розгорнутим кутом. Міра розгорнутого кута дорівнює 180°. Отже, якими б не були суміжні кути, сума їх мір дорівнює 180°.
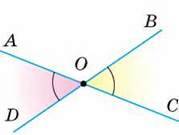
Два кути називають вертикальними, якщо сторони одного є доповняльними променями сторін другого.
Наприклад, якщо прямі АС і BD перетинаються в точці О, то кути AOD і ВОС – вертикальні (мал. 46). Кожний із них суміжний із кутом АОВ. Кути АО В і COD також вертикальні.
Теорема 2 Вертикальні кути рівні.
Доведення. Нехай AOD і ВОС – довільні вертикальні кути (мал. 46). Кожний із них суміжний із кутом АОВ. За теоремою про суміжні кути:
∠AOD + ∠AOB = 180° і ∠BOC + ∠AOB = 180°,
∠AOD = 180° – ∠AOB і ∠BOC = 180° – ∠AOB.
Праві частини цих рівностей однакові, тому ∠AOD = ∠BOC. А це й треба було довести.
Мал. 46
1 Детальні відомості про теореми, їх структуру та види прочитайте на с. 57 (& 8).
Для допитливих
1. Слово суміжні вживають не тільки щодо кутів.
Суміжний – той, що має спільну межу, прилеглий до чогось, сусідній. Можна говорити про суміжні кімнати, суміжні поля тощо. Стосовно кутів це поняття має особливий зміст.
Не будь-які два кути зі спільною межею називають суміжними. Наприклад, зображені на малюнку 47 кути АОВ і ВОС мають спільну сторону ОВ, але не є суміжними кутами.
Суміжні кути – це два кути, які перебувають у певному відношенні.
Один кут не може бути суміжним. Якщо говоримо, що якийсь кут суміжний, то обов’язково маємо закінчити думку: суміжний з яким кутом? Відношення суміжності кутів має таку властивість: якщо кут А суміжний з кутом В, то і кут В суміжний з кутом А.
Нехай кут А суміжний з кутом В, а кут В суміжний з кутом С. Що можна сказати про кути А і С? Вони або вертикальні, або кут С – той самий кут А (мал. 48).
2. Слово вертикальні також стосується не тільки кутів. Здебільшого вертикально розміщеним вважають продовгуватий предмет, розташований в напрямі виска (перпендикулярно до горизонту).
Завжди правильна властивість: якщо кут А вертикальний з кутом С, то і кут С вертикальний з кутом А.
Мал. 47
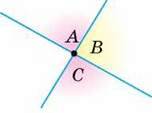
Мал. 48
Запитання і завдання для самоконтролю
1. Які кути називають суміжними?
2. Сформулюйте і доведіть властивість суміжних кутів.
3. Які кути називають вертикальними?
4. Сформулюйте і доведіть властивість вертикальних кутів.
Виконаємо разом
1. Знайдіть міри суміжних кутів, якщо один із них на 50° більший, ніж інший.
– Нехай міра меншого із суміжних кутів дорівнює х, тоді міра більшого кута – х + 50°. За властивістю суміжних кутів х + х + 50° = 180°, звідси х = 65°, а х + 50° = 115°. Отже, це кути 65° і 115°.
2. Один із чотирьох кутів, які утворилися при перетині двох прямих, удвічі більший від іншого. Знайдіть міру кожного з утворених кутів.
– При перетині двох прямих утворюються вертикальні і суміжні кути. Оскільки вертикальні кути рівні, то вони умову задачі не задовольняють. Робимо висновок: один із суміжних кутів удвічі більший за інший, їх міри – х і 2х. За властивістю суміжних кутів х + 2х = 180°, звідси х = 60°, а 2х = 120°. Відповідні їм вертикальні кути також дорівнюють 60° і 120°. Отже, це кути – 60°, 120°, 60°, 120°.
ЗАДАЧІ І ВПРАВИ
Виконайте усно
96. Назвіть пари суміжних кутів, зображених на малюнку 49.
97. Чи можна вважати суміжними кути КОВ і КОА, зображені на малюнку 49? А кути АОС і AOD?
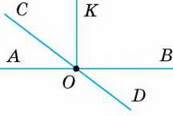
Мал. 49
98. Дано гострий кут А. Чи може бути гострим суміжний з ним кут? А прямим?
99. Дано тупий кут. Яким є суміжний з ним кут?
100. Сума кутів А і В дорівнює 180°. Чи суміжні вони?
101. Розгорнутий кут двома внутрішніми променями розбито на три менші кути. Чи можна їх уважати суміжними кутами?
102. Чи вертикальні кути АОВ і COD, зображені на малюнку 50?
103. Один із кутів, утворених при перетині двох прямих, дорівнює 100°. Знайдіть міри трьох інших кутів (мал. 51).
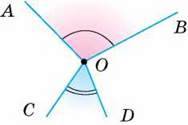
Мал. 50
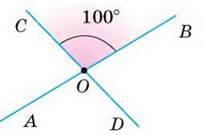
Мал. 51
А
104. Міра одного з двох суміжних кутів дорівнює 50°. Знайдіть міру іншого кута. Побудуйте ці кути.
105. Дано кут, міра якого дорівнює 160°. Знайдіть міру суміжного з ним кута. Побудуйте ці кути. Зафарбуйте їх різними кольорами.
106. Знайдіть міру кута, суміжного з кутом ABC, якщо:
А) ∠АВС = 34°; б) ∠ABC =111°;
В) ∠ABC = 13°13′; г) ∠ABC = 135°47′.
107. Доведіть, що якщо суміжні кути рівні, то вони прямі.
108. Знайдіть міри суміжних кутів, якщо один із них:
А) на 30° більший за інший;
Б) у два рази менший від іншого.
109. Знайдіть міри суміжних кутів, які відносяться як:
А) 4 : 5; б) 3 : 2.
110. Накресліть кут, що має 45°. Побудуйте вертикальний йому кут.
111. Сума мір двох вертикальних кутів дорівнює 120°. Знайдіть міру кожного з цих кутів.
112. Знайдіть міри кутів, утворених при перетині двох прямих, якщо міра одного з них дорівнює:
А) 50°; б) 110°; в) n°.
113. Перенесіть таблицю в зошит і заповніть її.
Даний кут | 10° | 50° | 60° | 90° | 120° | 170° |
Вертикальний із ним кут | ||||||
Суміжний із ним кут |
114. Перемалюйте в зошит малюнок 46 і подану нижче таблицю. Використовуючи малюнок, заповніть порожні клітинки таблиці.
∠AOD | 60° | 50°5′ |
∠AOB | 135° | 177° |
∠BOC | 39° | 33°33′ |
∠DOC | 97° | 99°9′ |
115. Чи можуть кути, що утворилися при перетині двох прямих, бути пропорційними числам:
А) 2, 3, 4 і 5;
Б) 5, 5, 5 і 8;
В) 2, 3, 2 i З;
Г) 1, 4, 1 і 4?
116. Накресліть куб ABC DA1B1C1D1. Чи можна вважати суміжними його кути АВВ1 і В1ВС1 Чому? Чому дорівнює міра кута, суміжного з кутом АВВ1?
117. Намалюйте три прямі так, щоб вони перетиналися в одній точці. Скільки пар вертикальних кутів утворилося?
118. Скільки пар вертикальних кутів і скільки пар суміжних кутів зображено на малюнку 52?
119. На малюнку 53 зображено три прямі, які перетинаються в точці О. Доведіть, що ∠1 + ∠2 + ∠З = 180°.

Мал. 52
Мал. 53
120. Знайдіть міри кутів, утворених при перетині двох прямих, якщо:
А) один із них на 50° більший за інший;
Б) один із них дорівнює половині іншого;
В) сума мір двох із цих кутів дорівнює 100°.
121. Кут АОВ має 180°, промінь ОМ ділить його на два кути, один із яких більший за інший на 20°. Знайдіть міри цих двох кутів, а також кут між їх бісектрисами.
122. Кути АОВ і ВОС – суміжні, ОМ – бісектриса кута ВОС. Знайдіть ∠AОВ, якщо:
А) ∠МОС = 30°; б) ∠МОС = 45°; в) ∠МОС = 60°.
123. Доведіть, що кути, суміжні з рівними кутами, рівні.
124. Знайдіть міру кута, якщо сума двох суміжних із ним кутів дорівнює 100°.
125. Кути АО В і ВОС – суміжні. ОМ – бісектриса кута АОB (мал. 54).
Знайдіть ∠МОВ, якщо:
А) ∠AOB – ∠ВОС = 40°;
Б) ∠AОВ : ∠ВОС = 5;
В) ∠AOB : ∠BOC = 5 : 4;
Г) ∠BOC становить  ∠AOB.
∠AOB.
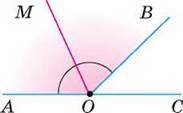
Мал. 54
Практичне завдання
126. Перегинаючи аркуш паперу, утворіть пару суміжних кутів і пару вертикальних кутів.
ВПРАВИ ДЛЯ ПОВТОРЕННЯ
127. Ребра двох кубів відносяться як 1 : 2. Як відносяться їх об’єми? А площі поверхонь?
128. Позначте на координатній площині точки А (1; -1), В (1; 3), С (5; 3); D (5; -1) і сполучіть їх послідовно відрізками. Як називається утворена фігура ABCD? Які з її сторін паралельні, а які – перпендикулярні?
129. Круг радіуса 3 см поділіть радіусами на б рівних секторів. Знайдіть площу одного такого сектора. На скільки вона менша від площі всього круга?
130. Фігура, зображена на малюнку 55, складається з 9 рівних листків. Знайдіть площу одного листка, якщо A, B, C, D – вершини квадрата з площею S.
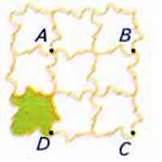
Мал. 55
Геометрія навколо нас

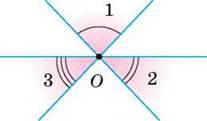
ЗАДАЧІ ЗА ГОТОВИМИ МАЛЮНКАМИ
А
1
Знайдіть пари суміжних кутів.
2
∠1 = 30°, ∠2 = 45°.
∠AOC, ∠BOC
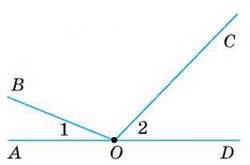
3
∠2 – ∠1 = 40°.
∠1, ∠2
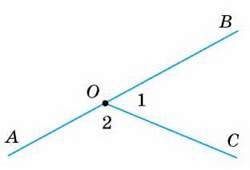
4
∠1 = 60°, ∠3 = 40°.
∠2, ∠4, ∠5, ∠6
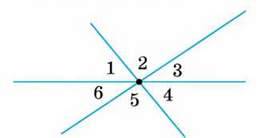
Б
1
∠1 = 120°, ∠2 = ∠3.
∠2, ∠AOM
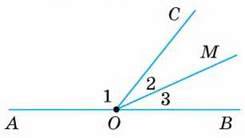
2
∠1 = 2∠2.
∠1, ∠2
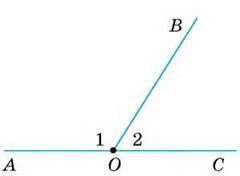
3
∠1 : ∠2 = 2 : 7.
∠1, ∠2
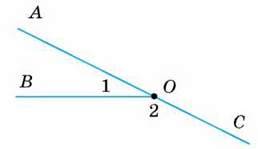
4
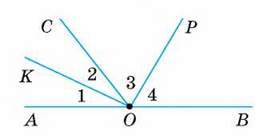
∠1 = ∠2, ∠3 = ∠4.
Довести: ∠KOP = 90°.