Тригонометричні функції кута
УРОК 5
Тема. Тригонометричні функції кута
Мета уроку: повторити означення тригонометричних функцій гострого кута прямокутного трикутника і ввести означення тригонометричної функції довільного кута.
І. Аналіз помилок, допущених у математичному диктанті та самостійній роботі.
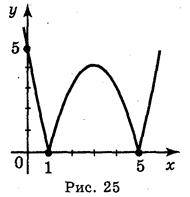
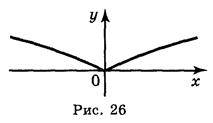
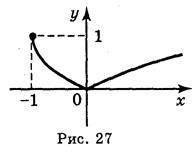
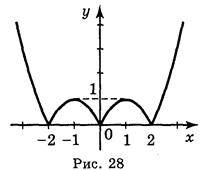
1. Побудуйте графіки функцій (індивідуальні картки):
А) 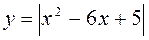 ; б)
; б) 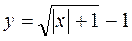 ; в)
; в) 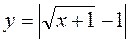 ; г)
; г) 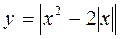 .
.
Відповідь: а) рис. 25; б) рис. 26; в) рис. 27; г) рис. 28.
2. Побудуйте графіки функцій (індивідуальні картки):
А) 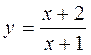 ; б)
; б) 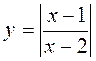
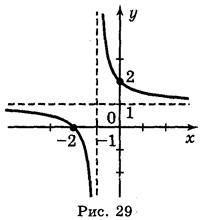
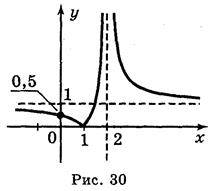
Відповідь: а) рис. 29; б) рис. 30.
II. Повторення відомостей про тригонометричні функції гострих кутів прямокутного трикутника.
Провести повторення шляхом фронтальної бесіди з використанням таблиці 3.

1. Дайте означення синуса гострого кута прямокутного трикутника.
2. Дайте означення косинуса гострого кута прямокутного трикутника.
3.
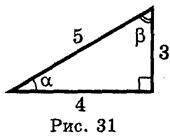
4. Користуючись рис. 31, знайдіть sin?, cos?, tg?, ctg?, sin?, cos?, tg?, ctg?.

5. Обчисліть:
А) 2 cos 60° +  cos 30°;
cos 30°;
Б) 3tg45°-tg60°;
В) 2 cos 30° + 6 cos 60° – 4 tg 45°;
Г) 2 ctg 60° – 2 sin 60°.
6. Спростіть:
A) (1 – cos?)(1 + cos?);
6) tg? – ctg? + sin2 ? + cos2 ?.
III. Повторення відомостей про тригонометричні функції довільного кута
У курсі геометрії для кутів від 0° до 180° було дано означення синуса, косинуса, тангенса за допомогою кола. Нагадаємо ці означення. Нехай дано коло радіуса R, центр якого знаходиться у початку координат. Відкладемо від додатної півосі у верхню півплощину кут?, друга сторона якого перетне коло в точці Р?(х; у) (рис. 32).
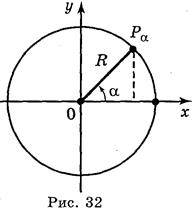
Синусом кута називається відношення ординати точки Р?(х; у) кола до його радіуса: 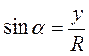 .
.
Косинусом кута називається відношення абсциси точки Р?(.х; у) кола до його радіуса: 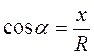 .
.
Тангенсом кута називається відношення ординати точки Р?(х; у) до її абсциси: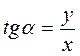 .
.
Котангенсом кута називається відношення абсциси точки Р?(х; у) до її ординати: 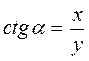 .
.
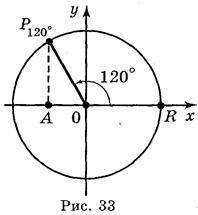
Приклад 1. Знайти sin?, cos?, tg?, ctg?, якщо? = 120°. Побудувавши точку Р120?, маємо (рис. 33):
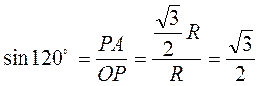 ;
; 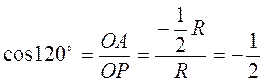 ;
; 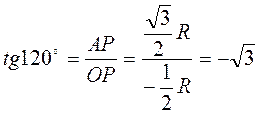 ;
; 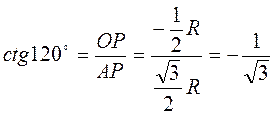 ;
;
Якщо будь-який кут розглядати як фігуру, утворену обертанням променя навколо своєї початкової точки у двох можливих напрямах (додатному – проти годинникової стрілки, від’ємному – за годинниковою стрілкою), то дане визначення можна використовувати для будь-яких кутів.
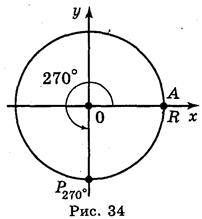
Приклад 2. Знайти sin?, cos?, tg?, ctg?, якщо? = 270°. При повороті на 270° навколо точки О радіус ОА, який дорівнює R, перейде в радіус ОР, тоді (рис. 34)
Р270?-(0; – R ) і, отже, sin 270° = 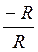 = -1, cos 270° =
= -1, cos 270° = 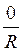 = 0, ctg270° =
= 0, ctg270° = 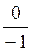 = 0 , tg 270° не має змісту.
= 0 , tg 270° не має змісту.
Із курсу геометрії відомо, що величина кута в градусах виражається числом від 0° до 180°. Кут Повороту може виражатися в градусах, яким завгодно дійсним числом від – до +
до + .
.
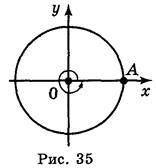
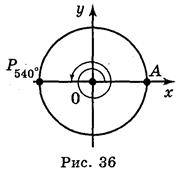
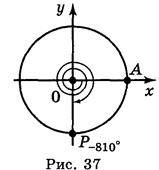
Приклад 3. Якщо початковий радіус ОА зробив повний оберт проти годинникової стрілки, то кут повороту буде дорівнювати 360° (рис. 35). Якщо початковий радіус ОА зробив півтора оберти проти годинникової стрілки, то кут повороту буде дорівнювати 540? (рис. 36). Якщо початковий радіус ОА зробив два повних оберти і чверть оберту за годинниковою стрілкою, то кут повороту буде дорівнювати 2 (-360°) – 90° = – 810° (рис. 37).
Розглянемо радіуси ОА і ОВ. Існує безліч кутів повороту, при яких початковий радіус ОА переходить у радіус ОВ (рис. 38). Нехай <AОВ = ?, тоді відповідні кути повороту будуть дорівнювати? + 360°n, де n – ціле число (n  ?).
?).
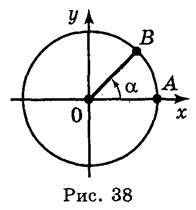
Якщо початковий радіус переходить у радіус ОВ при повороті на кут а, то в залежності від того, у якій четверті буде радіус 0B, кут? називають кутом цієї чверті. Так, якщо 0° < ? < 90°, то? – кут І чверті; якщо 90° < ? < 180°, то? – кут II чверті; якщо 180° < ? < 270°, то? – кут III чверті; якщо 270° < ? < 360°, то? – кут IV чверті. Кути 0°; ±90°; ±180°; ±270°; ±360° не відносяться ні до якої чверті.
У курсі геометрії було доведено, що значення синуса, косинуса і тангенса кута?, де 0° < ? < 180° залежить тільки від? і не залежить від довжини R. І в загальному вигляді sin?, cos?, tg?, а також ctg? залежать тільки від кута?.
Вирази sin? і cos?, визначені для будь-яких а, так само як для будь-якого кута повороту, можна знайти відношенням 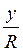 і
і 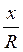 .
.
Вираз tg? має смисл при будь-яких а, крім кутів повороту ±90°; ±270°; ±450°, тобто? 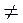 90°+180° n, (n
90°+180° n, (n  ?).
?).
Вираз ctg? має смисл при будь-яких а, крім кутів повороту 0°; ±180°; ±360°.., тобто, ? 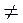 180° n, (n
180° n, (n  ?).
?).
Кожному допустимому значенню? відповідає єдине значення sin?, cos?, tg?, ctg?, тому синус, косинус, тангенс, котангенс є функціями кута?. Їх називають тригонометричними функціями.
Виконання вправ
1. Чому дорівнюють кути повороту, які показано на рисунку 39.
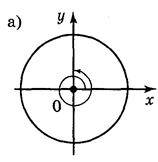
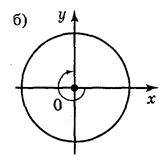
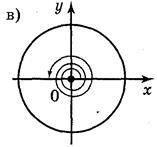
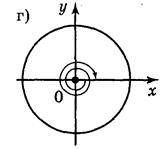
Рис. 39
2. Накресліть коло із центром у початку координат і побудуйте кут повороту, що дорівнює: а) 135°; б) -120°; в) 540°; г) -810°.
3. Запишіть всі кути поворотів, при яких радіус ОА переходить у радіус ОВ (рис. 40).
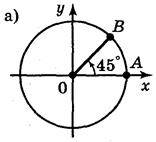
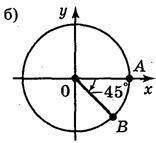
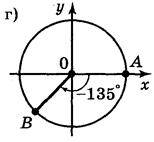
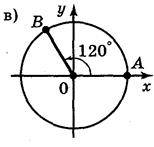
Рис. 40
4. Побудуйте коло з центром у початку координат і кути повороту, що дорівнюють:
А) 90° + 360° n, (n  Z);
Z);
Б) 180° + 360° n, (n  Z);
Z);
В) -90? + 180° n, (n  Z);
Z);
Г) ±60° + 360? n, (n  Z).
Z).
5. Визначте, кутом якої чверті є кут?, якщо кут а дорівнює:
А) 181°; б) 179°; в) 271°; г) 361°; д) 345°; є) 800°.
6. Серед кутів повороту 790°; 500°; -30°; 1580°; -220°; -290° знайдіть такі, при яких початковий радіус займе таке саме положення, як і при повороті на кут: а) ? = 70°; 6) ? = 140°.
7. Накресліть коло з центром на початку координат і радіусом R = 5 см. Поверніть початковий радіус на кут? і знайдіть наближене значення sin?, cos?, tg?, ctg?, якщо? = 50°; 175°; -100°.
IV. Підсумок уроку
V. Домашнє завдання
Розділ І § 2. Запитання і завдання для повторення № 32-34. Вправи № 4, 5.
