Відносність механічного руху. Закон додавання швидкостей
КІНЕМАТИКА
Урок № 4
Тема. Відносність механічного руху. Закон додавання швидкостей
Мета: перевірити знання графіків руху і вміння їх будувати та читати; сформувати знання про відносність руху і спокою тіла, сформулювати правило додавання переміщень і швидкостей під час відносного руху, виробити вміння визначати швидкість і переміщення тіл відносно різних систем відліку, переконати учнів у життєвій необхідності таких умінь; сформувати знання про те, що рух – універсальна властивість матерії і водночас механічний рух має відносний
Тип уроку: урок комбінований.
Унаочнення: демонстрування руху кульки в трубці з рідиною відносно стола і рухомого покажчика, візків відносно стола і один відносно одного та дослідів відеофільм “Системи відліку і відносність руху”.
ХІД УРОКУ
І. Самостійна робота “Прямолінійний рівномірний рух”
Початковий рівень
1. Подайте в метрах за секунду швидкість 54 км/год.
2. Обчисліть швидкість лижника, який пройшов 14 км за 2 год.
Середній рівень
1. Скільки часу потрібно швидкому поїзду завдовжки 150 м, щоб проїхати міст довжиною 850 м, якщо швидкість поїзда дорівнює 72 км/год.
2.
Достатній рівень
1. Уздовж осі Ox рухаються два тіла, координати яких змінюються згідно з формулами: x1 = 10 + 2t і x2 = 4 + 5t. Як рухаються ці тіла? У який момент часу тіла зустрінуться? Знайдіть координату точки зустрічі.
2. Уздовж осі Ox рухаються два тіла, координати яких змінюються згідно з формулами: х1 = 5t і х2 = 150 – 10t. Як ці тіла рухаються? У який момент часу тіла зустрінуться? Знайдіть координату точки зустрічі.
Високий рівень
1. Рух матеріальної точки в площині XOY описується рівняннями: x = 2t, y = 4 – 2t. Побудуйте траєкторію руху.
2. Велосипедист проїхав 3/4 відстані від селища А до селища Б за одну годину. З якою швидкістю він рухався, якщо, збільшивши швидкість до 25 км/год., він за наступну годину дістався до селища Б і повернувся в селище А?
II. Вивчення нового матеріалу
Новий матеріал пояснюють у ході уроку з використанням демонстраційного експерименту.
Поняття відносності руху уже випливає з означення механічного руху. Одні тіла рухаються відносно інших. Не буває абсолютного руху або абсолютного спокою. Тіло, відносно якого розглядається зміна положення тіла, називають тілом відліку. Приклади тіл відліку: кімната будинку, купе вагона, Земля для руху супутника, Сонце для руху Землі.
Відносність руху означає, що координати тіла, швидкість, вид траєкторії залежать від того, відносно якої системи відліку розглядається рух.
Нехай система відліку (а’) рухається зі швидкістю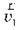 
відносно іншої системи (а), а відносно системи а’ тіло рухається зі швидкістю 
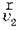, тоді швидкість тіла відносно нерухомої системи 
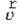дорівнює геометричній сумі швидкостей (рис. 1 ):
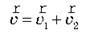
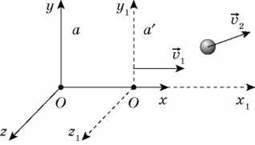
Рис. 1
Сукупність виразів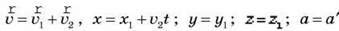 
називається перетвореннями Галілея.
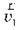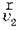Якщо точка бере участь у двох незалежних прямолінійних і рівномірних рухах зі швидкостями і (рис. 2), то швидкість результуючого руху 
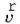визначають за формулою: 
.
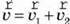Це закон додавання швидкостей: швидкість руху тіла відносно нерухомої системи відліку дорівнює геометричній сумі швидкості цього тіла відносно рухомої системи відліку 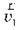і швидкості самої рухомої системи відліку 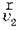відносно нерухомої системи.
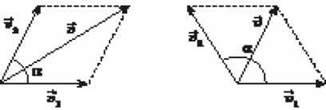
Рис. 2
Модуль результуючої швидкості човна 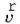у випадку довільного кута? між швидкістю течії річки 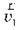і швидкістю човна відносно течії 
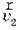дорівнює: 
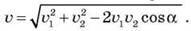Якщо кут? прямий, то 
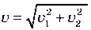, якщо човен рухається за течією 
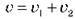, проти течії 
.
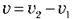На закінчення уроку учні переглядають відео-фрагмент “Системи відліку і відносність руху”.
IV. Підсумок уроку
Закінчити речення.
– Я дізнався, що…
– Тепер я можу…
– Отже,…
V. Домашнє завдання
1. Вивчити конспект уроку; відповідний параграф підручника; скласти опорний конспект. Повторити матеріал з математики про теореми синусів та косинусів, дії з векторами.
2. Розв’язати задачі.
– Рухаючись рівномірно прямолінійно, тіло за 10 с подолало 500 см. За скільки годин це тіло, рухаючись із тією самою швидкістю й у тому самому напрямі, подолає шлях 60 км?
– Уздовж осі Ox рухаються два тіла, координати яких змінюються згідно з формулами: x1 = 5 + 2t і x2 = -4 + 5t. Як рухаються ці тіла? У який момент часу тіла зустрінуться? Знайдіть координату точки зустрічі.
(1 votes, average: 5.00 out of 5)
Loading...