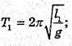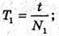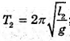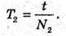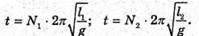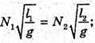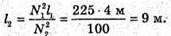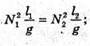Вправа 23
Вправа 23
1. Дано: I = 1м G = 10 м/с2 | Розв’язання: За формулою періоду математичного маятника Маємо
Відповідь: період коливань маятника ≈2 с. |
Т – ? |
2. Дано: Т = 1с G = 10 м/с2 | Розв’язання:
Звідси Обчислимо значення:
Відповідь: довжина маятника |
L – ? V – ? |
З. Дано: А = 5 см = 0,5 м T = 1 хв = 60 с N = 150 φ0 = 45° T1 = 0,2 с X = x(t) X(t1) – ? | Розв’язання: Рівняння гармонійних коливань маятника х – A sin(ω + φ0).
ω = 2πν = 2π ? 2,5 Гц = 5π с-1, Отже,
Відповідь: |
4. Дано: Gпол ≈ 9,83 м/с2 Gекв ≈ 9,78 м/с2 | Розв’язання: За формулою 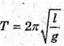 маємо маємо 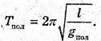 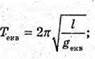 Отже,
Текв ≈ 1,0026 Тпол Відповідь: 3 хв 48 с. |
|
5. Дано: N = 24 T = 30 с | Розв’язання:
Відповідь: період коливань 1,25 с, частота коливань 0,8 Гц. |
Т – ? V – ? |
6 . Дано: L = 98 м G = 9,8 м/с2 α = 5° | Розв’язання: За формулою
А = l sin α = 98 м? sin 5° = 8,5 м. Відповідь: частота 0,05 Гц, амплітуда 8,5 м. |
V – ? А – ? |
7. Дано: V3 = 0,5 Гц
| Розв’язання:
Відповідь: частота коливань на Місяці ≈ 0,2 Гц. |
V M – ? |
8. Дано: L1 = 4 м N1 = 15 N2 = 10 T1 = t2 = t | Розв’язання: За формулою періоду маятника
Звідси маємо: Відповідь: довжина другого маятника 9 м. |
L2-? |
9. Дано: Х = 3,5 cos 4πt T = 5 с | Розв’язання: За рівнянням гармонійних коливань х= A cos(ωt + φ0) Маємо: А = 3,5 м. ω = 4π с-1; φ0 = 0. При t = 5c x = 3,5 cos 4π ? 5 = 3,5 cos 20π; φ = 20π. Відповідь: амплітуда коливань 3,5 м, циклічна частота 4π с-1, фаза коливань через 5 с після початку коливань 20π. |
А -? ω – ? φ – ? |




 (1 votes, average: 5.00 out of 5)
(1 votes, average: 5.00 out of 5)Related posts:
- Вправа 22 Вправа 22 1. Дано: Т = 1 кг Х = 30 см = 0,3 м G = 10 м/с2 Розв’язання: ω = 2πν = 2 · 3,14 · 1 Гц = 6,28 с-1. Відповідь: період 1 с, частота 1 Гц, колова частота 6,28 с-1 Т – ? V – ? ω – ? 2. Дано: […]...
- Вправа 25 Вправа 25 1. Дано: С = 2 пФ = = 2 ? 10-12Ф L = 0,5 мкГн = = 0,5 ? 10-6 Гн Розв’язання: За формулою обчислимо значення Періоду: Отже, Відповідь: частота коливань у контурі 160 МГц. V – ? 2. Дано: С = 1 мкФ = = 10-6 Ф U = 225 В L […]...
- Вправа 26 Вправа 26 1. Дано: С; λ1 Розв’язання: За формулою λ – v? Т, маємо λ1 – сТ, λ2 = vТ. Із маємо λ1 = 9λ2; λ1= 9 · vΤ. Отже, сТ = 9 · vΤ, звідси Відповідь: швидкість поширення зменшиться у 9 разів. 2. Дано λ = 500 м T = T V = 3000Гц […]...
- Вправа 29 Вправа 29 1. Дано: F = 25 см D = 25 см Розв’язання: За формулою лінзи Відповідь: фокусна відстань лінзи 12,5 см. F – ? 2. Дано: D = 60 см F = 50 см Розв’язання: За формулою лінзи звідси F = 300 см. Відповідь: зображення буде знаходитися на відстані 300 см. F – ? […]...
- Механічні коливання й хвилі. Коливання – КОЛИВАННЯ Й ХВИЛІ Формули й таблиці ФІЗИКА КОЛИВАННЯ Й ХВИЛІ Механічні коливання й хвилі Коливання Частота коливань ν – частота коливань, ; N – число повних коливань, за одиницю часу t, . Період коливань Т – час одного повного коливання, . Циклічна частота ω – число повних коливань за час 2πА, . Рівняння гармонійних коливань Проекція швидкості Проекція […]...
- Вправа 24 Вправа 24 1. Дано: V = 20 м/с Т = 0,5 с Розв’язання: Довжину хвилі можна визначити за формулою λ = v? T Обчислимо значення: λ = 20 м/с? 0,5 с = 10 м. Відповідь: довжина хвилі 10 м. λ – ? 2. Дано: λ = 300 м Т = 15 с V – ? […]...
- Вправа 32 Вправа 32 1. Дано: R = 5,29 · 10-11 м L = 1,6 · 10-19 Кл ε0 = 8,85 · 10-12 Φ/м Розв’язання: Відповідь: Еп= -4,4 · 10-18 Дж; Еκ= 2,2 · 10-18 Дж; Е= -2,2 · 10-11 Дж Εκ – ? Εп – ? Ε – ? 2. Дано: ? Ε = 2,5 еВ […]...
- Вправа 19 Вправа 19 1. Дано: S = 100 см2 = = 10-2 м2 В = 1 Тл α = 0° ?t = 0,01 с Розв’язання: Зміна магнітного поля спричинить ЕРС індукції, яка за законом електромагнітної індукції дорівнює За формулою? ф = ?В? S? cos α. Початковий магнітний потік ф1= BS cos α. Після зникнення магнітного поля […]...
- Лабораторна робота № 5. ДОСЛІДЖЕННЯ КОЛИВАНЬ НИТЯНОГО МАЯТНИКА Тип уроку: урок формування практичних навичок. Мета: сформувати в учнів навички визначати амплітуду, період і частоту коливань маятника; переконатися на досліді, що частота й період коливань маятника не залежать від амплітуди його коливань і маси тягарця, проте залежать від довжини нитки; виховувати в учнів охайність під час проведення експерименту, дбайливе ставлення до лабораторного обладнання; вчити […]...
- КОЛИВАЛЬНИЙ РУХ. АМПЛІТУДА КОЛИВАНЬ. ПЕРІОД КОЛИВАНЬ. МАЯТНИКИ Тип уроку: комбінований урок. Мета: надати учням уявлення про коливальний рух, ввести поняття амплітуди, періоду та частоти коливань; ознайомити учнів з видами маятників; показати практичне застосування маятників у техніці, в побуті. Обладнання та наочність: коливання вантажу на нитці та на пружині, запис коливального руху, механічний годинник із маятником. Відеофрагмент: коливання математичного та пружинного маятників, коливання […]...
- Вправа 11 Вправа 11 1. Дано: С = 200 мкФ = 2 ? 10-4 Ф?φ = 1000 В Розв’язання: Енергія конденсатора визначається за формулою: Перевіримо одиниці фізичних величин: Підставимо числові значення: Відповідь: енергія конденсатора 100 Дж. W – ? 2. Дано: Q = 4,8 ? 10-3 Кл ?φ = 600 В Розв’язання: Енергія конденсатора визначається за формулою: […]...
- Вправа 31 Вправа 31 1. Дано: λ1= 400 нм = = 4 · 10-7 м λ2 =760 нм = = 760 · 10-9 м С = З 108 м/с А = 6,626 · 10-34 Джс Розв’язання: Обчислимо значення: Відповідь: 5 ? 10-19 Дж; 2,6 · 10-19 Дж; 1,66 ? 10-27 кг(м/с); 8,7 ? 10-28 кг(м/с); 5,5 ? […]...
- ЛАБОРАТОРНА РОБОТА № 4 ЛАБОРАТОРНА РОБОТА № 4 Тема роботи: Дослідження коливань маятника. Мета: дослідити залежність періоду коливань маятника від амплітуди коливань, маси та довжини маятника. Обладнання: невеликі важки різної маси; штатив; лінійка з міліметровими поділками; секундомір. Хід роботи 1. Підвісимо важок на нитці до лапки штатива. 2. Відхилимо важок від положення рівноваги на невеликий кут і. відпустимо. 3. […]...
- Вправа 13 Вправа 13 1. Дано: R = 10 см = 0,1 м І = 600 А Розв’язання: Магнітна індукція поля прямого провідника обчислюється за формулою Перевіримо одиниці фізичних величин: Підставимо числові значення: Відповідь: магнітна індукція поля 1,2 мТл. В – ? 2. Дано: R = 10 см = 1 м В = 4 ? 10 -6 […]...
- Вправа 30 Вправа 30 1. Умова максимуму ?d = k? λ; ?d = 3 мкм. λ1 = 0,75 мкм; Умова максимуму виконується λ2 = 0,6 мкм; Умова максимуму виконується. λ3 = 0,5 мкм; Умова максимуму виконується. λ4 = 0,667 мкм; Умова максимуму не виконується. λ5 = 0,545 мкм; Умова максимуму не виконується. λ6 = 0,461 мкм; Умова […]...
- Вправа 18 Вправа 18 1. Дано: S = 40 см2 = = 4 · 10 -3 м2 В = 0,2 Тл Розв’язання: Магнітний потік, що проходить крізь поверхню, визначається за формулою Ф = BS. Перевіримо одиниці фізичних величин: [Ф] = Тл · м2 = Вб. Підставимо числові значення: Ф = 0,2 · 4 · 10 -3 = […]...
- Вправа 9 Вправа 9 1. Дано: S = 15 см2 = = 15 · 10 -4 м2 D = 0,02 см = = 2 · 10-4 ε = 6 Розв’язання: Ємність плоского конденсатора визначається з формули Перевіримо одиниці фізичних величин: Підставимо числові значення: Відповідь: ємність конденсатора 400 пФ. C – ? 2. Дано: С = 1 мкФ […]...
- Вправа 20 Вправа 20 1. Дано: ε = 30 В Розв’язання: Згідно із законом ЕРС самоіндукції: Звідси Визначимо значення: Відповідь: індуктивність соленоїда 0,375 Гн. L – ? 2. Дано: L = 2 Гн ε= 20 В Розв’язання: Згідно із законом ЕРС самоіндукції: Звідси: Визначимо значення: Відповідь: швидкість зміни струму в обмотці електромагніту 3. Дано: ?І = 2А […]...
- Вправа 28 Вправа 28 1. Дано: V = 200 000 км/с = = 2 ? 108 м/с С = 3 ? 108 м/с Розв’язання: Показник заломлення Обчислимо значення: Відповідь: показник заломлення скла 1,5. N – ? 2. Дано: α = 25° V = 2,4 · 105 км/с = = 2,4 · 108 м/с С = 3 ? […]...
- Вправа 15 Вправа 15 1. Дано: V = 103 м/с Q = 2е Е – 1,6 ? 10 -6 Кл В = 0,2 Тл Розв’язання: Значення сили Лоренца визначається за формулою Fл= qvB. Оскільки q = 2е, то Fл = 2еvB. Перевіримо одиниці фізичних величин: Підставимо числові значення: Fл л = 2· 1,6 · ? 10 -19 […]...
- Вправа 1 Вправа 1 1. Дано: Q = 0,2 мкКл = 2 ? 10-7 Кл Розв’язання: Сила, з якою електричне поле діє на заряджене тіло, дорівнює: Модуль цієї сили F = qE. Перевіримо одиниці фізичних величин: Підставимо числові значення: F = 8 ? 2 ? 10-7 = 16 ? І0-7 = 1,6 ? 10-6 (Н). Відповідь: поле […]...
- Вправа 205-210 № 205. Гідроксиди – сполуки металічних елементів із загальною формулою М(ОН)n (М – металічний елемент). Основи – це гідроксиди Натрію, Калію, Барію, кальцію, інших металічних елементів. Луги – це розчинні у воді основи. № 206. № 207. № 208. Відповідь: a) 56,3 %; б) 65,3 %. № 209. Дано: Розв’язання 1. Обчислимо масу NaOH: (бо […]...
- Вправа 14 Вправа 14 1. Дано: L = 0,5 м α = 90° В = 2 ? 10 -62 Тл FA = 0,15 Н Два паралельні провідники, якими йде струм одного напряму, притягуються під дією сили Ампера. На два паралельні пучки електронів також діє сила Ампера, але вона менша за кулонівську силу відштовхування, тобто FA < Fкул. […]...
- Вправа 10 Вправа 10 1 . Дано: С1 = 2 пФ = 2 ? 10-12 Ф С2 = 5 пФ = 5 ? 10-12 Ф С3 = 10 пФ = 10 ? 10-12 Ф С4= 20 пФ = 2 ? 20-12 Ф Розв’язання: При паралельному з’єднанні конденсаторів їх загальна ємність дорівнює:Спар. = С1 + С2 +.C3+ С4 […]...
- Вправа 27 Вправа 27 1. Дано: α = 25° Розв’язання: Із закону відбивання світла β – α = 90° – β. Отже, 2β = 90°” + α; Відповідь: освітити дно криниці можна дзеркалом, яке поставлене під кутом 57,5° до горизонту. β-? 2. Плоске дзеркало має бути заввишки АВ – людина; А1В1 – зображення людини у дзеркалі; точка […]...
- Вправа 16 Вправа 16 І = 0,25 м B = 0,2 Тл = = 8 ?10 -3 Тл α = 30° εі -? 1. За правилом правої руки визначаємо напрямок Індукційного струму: Розв’язання: Оскільки провідник рухається рівномірно в однорідному Магнітному полі, то значення ЕРС індукції визначається за Формулою: εі = Blv sin α. Перевіримо одиниці фізичних величин: […]...
- Вправа 195-204 № 195. Відповідь: m(р. р.) = 6 г. № 196. Дано: Розв’язання 1. Обчислимо m розчину: 2. Обчислимо масову частку розчиненої речовини: Відповідь: ω(цукру) = 0,2 або 20 %. № 197. M (р-ну), г M (р. р.), г M (води), г ω(р. р.) 400 8 392 0,02 або 2 % 500 40 460 0,08 або […]...
- Вправа 7 Вправа 7 1. Дано: φ = 6 ? 103 В Q = 3 ? 10-8 Кл Розв´язання: Відповідно до означення електроємність кульки Перевіримо одиниці фізичних величин: Підставимо числові значення: Відповідь: електроємність кульки 5 пФ. С – ? 2. Дано: φ = 30 В С = 150 пФ = = 150 ? 10-12 Ф Розв’язання: Відповідно […]...
- Вправа 12 Вправа 12 1. Дано: ε – 12 В /=2А, U = 10 В Розв’язання: Згідно із законом Ома для ділянки кола: Звідси Згідно із законом Ома для повного кола: Звідси Перевіримо одиниці фізичних величин: Підставимо числові значення: Відповідь: внутрішній опір джерела 1 Ом, опір навантаження 5 Ом. R – ? R – ? 2. Дано: […]...
- Вправа 5 Вправа 5 1. Дано: Q = 2мкКл = = 2 ? 10-6 Кл R = 3 м Розв’язання: Потенціал електричного поля точкового заряду дорівнює: Перевіримо одиниці фізичних величин: Підставимо числові значення: Відповідь: потенціал поля 6 кВ. φ-? 2. Дано: R = 30 м φ = 3000 В Розв’язання: Потенціал електричного поля точкового заряду Дорівнює: Звідси […]...
- Вправа 8 Вправа 8 1. Дано: U =1,5 В Q = 30 нКл = = 3 · 10-8 Кл Розв’язання: Ємність конденсатора дорівнює Перевіримо одиниці фізичних величин: Підставимо числові значення: Відповідь: ємність конденсатора 20 нФ. С – ? 2. Дано: Δφ = 1000 В С = 3 мкФ = = 3 · 10-6 Ф Розв’язання: Ємність конденсатора […]...
- Вправа 6 Вправа 6 1. Дано: Q = 0,012 Кл А = 0,36 Дж Розв’язання: Різниця потенціалів між двома точками електричного поля: Перевіримо одиниці фізичних величин: Підставимо числові значення: Відповідь: різниця потенціалів 30 В. ?φ – ? 2. Дано: Q = 4,6 ? 10 6 Кл ?φ = 2000 В Розв’язання: Різниця потенціалів між двома точками електричного […]...
- Вправа 3 Вправа З 1. Дано: Q1 = q2 = 10-7 Кл R = 0,1 м Розв’язання: Згідно із законом Кулона, сила взаємодії між кульками дорівнює: Оскільки q1 = q2 , то Перевіримо одиниці фізичних величин: Підставимо числові значення: Відповідь: сила взаємодії 9 мН. F – ? 2. Дано Q 1 = 0,66 ? 10-7 Кл Q […]...
- Вправа 21 Вправа 21 1. А) Електричний струм, породжує магнітне поле, енергія якого переходить у механічну енергію; Б) в) енергія магнітного поля електромагніту переходить у механічну енергію; Г) енергія магнітного поля постійного магніту переходить у механічну енергію. 2. Дано: R = 8,2 Ом U = 55 В L = 25 мГн = = 25 ? 10-3Гн Розв’язання: […]...
- ПІДСУМКИ РОЗДІЛУ ІІ Розділ ІІ Механічний рух ПІДСУМКИ РОЗДІЛУ ІІ – Механічним рухом називають зміну положення тіла відносно інших тіл з часом. – Швидкість руху, шлях або час можна обчислити, користуючись формулою v = . – Переміщення, швидкість і траєкторія тіла залежать від того, відносно яких тіл відліку визначається рух. – Швидкість тіла відносно нерухомої системи відліку дорівнює […]...
- Вправа 131-138 № 131. А) Кисень – проста речовина Оксигена; Б) вода утворена Гідрогеном і Оксигеном; В) молекула кисню складається із двох атомів Оксигену; Г) у результаті фотосинтезу рослини поглинають вуглекислий газ, а виділяють кисень. № 132. У повітрі найбільше газів: – азот N2 – 78,08 %; – кисень O2 – 20,95 %. № 133. Атоми Оксигену […]...
- ТЕСТ 11. МЕХАНІЧНІ КОЛИВАННЯ І ХВИЛІ Фізика підготовка до ЗНО комплексне видання КОЛИВАННЯ І ХВИЛІ. ОПТИКА ТЕСТ 11. МЕХАНІЧНІ КОЛИВАННЯ І ХВИЛІ Завдання 1-14 мають чотири варіанти відповідей, із яких тільки одна відповідь є правильною. Виберіть правильну, на вашу думку, відповідь. 1. Як називається рух, за якого траєкторія руху тіла повторюється через однакові проміжки часу? 2. Хлопчик, який гойдається на гойдалці, […]...
- Механічні коливання 5. Механіка 5.6. Механічні коливання Механічні коливання – це періодичні повторення переміщень матеріальної точки, за яких вона рухається по якій-небудь траєкторії почергово у двох протилежних напрямах відносно положення стійкої рівноваги. Гармонічні коливання – це механічні коливання, що відбуваються під дією сили, яка пропорційна зміщенню відносно положення рівноваги і спрямована протилежно до нього. Амплітуда – найбільше […]...
- Вправа 4 Вправа 4 1. Дано: Q = 4мкКл = = 4 ? 10-6 Кл L = 5 см = 5 ? 10-2 м α = 60о Розв’язання: Сила, що діє на тіло з боку електричного поля, виконує роботу, що дорівнює: Модуль сили дорівнює: F = qE. Отже, Перевіримо одиниці фізичних величин: Підставимо числові значення: Відповідь: поле […]...
- МАТЕМАТИЧНИМ МАЯТНИК. ПЕРІОД КОЛИВАНЬ МАТЕМАТИЧНОГО МАЯТНИКА МЕХАНІЧНІ І ЕЛЕКТРОМАГНІТНІ КОЛИВАННЯ І ХВИЛІ Розділ 3 Коливання і хвилі § 22. МАТЕМАТИЧНИМ МАЯТНИК. ПЕРІОД КОЛИВАНЬ МАТЕМАТИЧНОГО МАЯТНИКА З попередніх класів ви знаєте, що математичним маятником вважають точкове тіло, підвішене до нерозтяжної і невагомої нитки. Математичний маятник – це поняття абстрактне, тому що: розміри кульки набагато менші за довжину нитки, цими розмірами можна нехтувати […]...
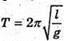
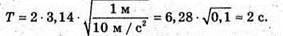
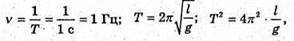
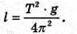
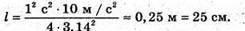
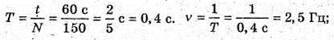
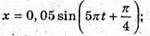
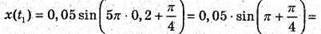
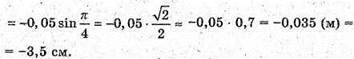
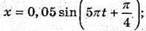 x(t1) = -3,5 см.
x(t1) = -3,5 см.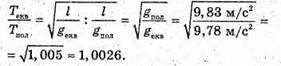
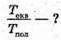
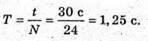
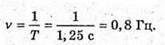
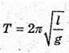 Маємо
Маємо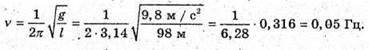
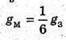
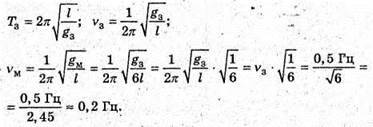
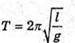 маємо:
маємо: