Головна ⇒ 📌ГДЗ з математики ⇒ Вправи 525-574

Вправи 525-574

525.

Вправи 525 574

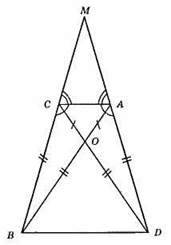
АВ = CD; AO : OB = CO : OD; ?СОВ = ?AOD (за двома сторонами і кутом МІНІ ними). З рівності трикутників маємо: BC = AD. ?ВСА = ?DAC.

1) АС – спільна сторона; 2) AB = CD; 3) BC = DA; ∠MCA = ∠MAC; отже, ∠A = ∠C; ?CMА – рівнобедрений; МС = AM; ВМ = BC + CM; MD = МА + AD; ВМ = MD; ?BMD – рівнобедрений.

526.

Вправи 525 574

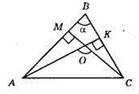
?ABC; ∠B = α; AK ⊥ BC; AK – висота? ABC; CM ⊥ AB; CM – висота? ABC; ∠AOC – кут між висотами, або ∠KOC – кут між висотами. ∠AOK = 180° – α або ∠KOC = α.

527.

Вправи 525 574

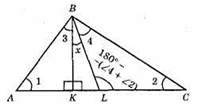
ВК – висота, BL – бісектриса

кута В. ∠ABK = ∠3; ∠KBL = ∠x; ∠LBC = ∠4; ∠3 + ∠x = ∠4; BL – бісектриса; ?BKL – прямокутний. ∠BLC – зовнішній кут. ∠BLC = 180° – (∠4 + ∠2); x + 90° = 180° – (∠4 + ∠2); x = 90° – (∠4 + ∠2); x = 90° – (∠3 + x + ∠2) = 90° – ∠3 – x – ∠2; 2x = 90° – ∠3 – ∠2;

?ABK; ∠1 = 90° – ∠3; 2x = 90° – ∠3 – ∠2; 2x = ∠1 – ∠2; x = 1/2(∠1 – ∠2), що і треба довести.

528.

Вправи 525 574

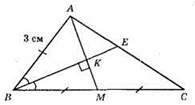
?АВС; AM – медіана? АВС; ВМ = MC; AB = 3 см; ?ABM – рівнобедрений, ВК ⊥ АМ; ∠ABK = ∠MBK; ВК – бісектриса і висота; ВК ⊥ АМ; AB = ВМ = 3 см; ВМ = MC = 3 см; ВС = 6 см.

Відповідь: 6 см.

529.

Вправи 525 574

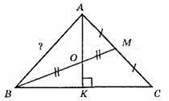
AK ⊥ ВС;

?ABC; ВО = ОМ; АС = 10 см; AM = MC = 5 см; AB = AM = 5 см.

Відповідь: 5 см.

530. Задача має два розв’язки. ?АВК і? МВС – рівнобедрені. AB = 2 + 7 = 9 (см) або AB = 7 – 2 = 5 (см).

531.

Вправи 525 574

?АВС; AB < ВС < АС; ∠1 = х; ∠2 = 2х; ∠3 = x + 100°; х + 2х + х + 100° = 180°; 4х = 180° – 100°; 4х = 80°; х = 80° : 4; х = 20°. ∠x = 20°; ∠2x = 40°; ∠3 = 120°. ∠B – найбільший кут. ∠B = 120°.

533. а) з відрізків завдовжки 2; 3; 4; 5 можна скласти 3 трикутники: 1) 3; 4; 5; 2) 2; 3; 4; 3)2; 4; 5;

Б) з відрізків завдовжки 2; 3; 4; 5; 6; 7 можна скласти 13 трикутників.

534. а) ОА = R;

Вправи 525 574

Б) ОА < R;

Вправи 525 574

В) ОА > R.

Вправи 525 574

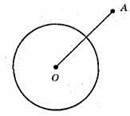
535. а) одна точка;

Вправи 525 574

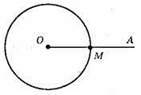
Б) дві точки.

Вправи 525 574

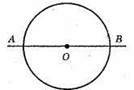
536.

Вправи 525 574

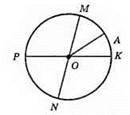
MN і PK – діаметри; MN = PK = d; OA = R = d/2.

537.

Вправи 525 574

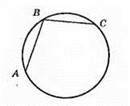
АВ і BC – не можуть бути діаметрами.

538.

Вправи 525 574

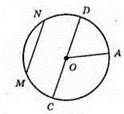
OA = 3 CM; CD = 6 CM; CD – діаметр; MN – хорда.

540. Радіус кола 8 см; діаметр 16 CM.

541. R = 5,5 см.

542.

Вправи 525 574

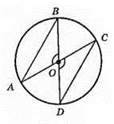
АС і BD – діаметри кола; ?АОВ = ?COD; AO = CO; ВО = OD (радіуси кола); ∠АОВ = ∠COD (вертикальні кути); ?АОВ = ?COD за першою ознакою рівності трикутників.

AB = 8 CM; АС = 14 см; АО = 7 см; DC = AB; ОС = ОА = 7 см; Р? COD = ОС + OD + DC = 7 см + 7 см + 8 см = 22 см.

543.

Вправи 525 574

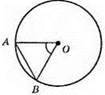
AO = BO – радіуси кола; ∠АОВ = 60°; AB = 6 см; ?АОВ – рівносторонній; АО = OB; ∠A = ∠B = (180° – 60°) : 2 = 60°;

∠A = ∠B = ∠О; AO = OB = AB = 5 CM; P? AOB = 5 CM.

544.

Вправи 525 574

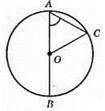
AB – діаметр; AB = 2 R; AC – хорда, АС = R; ∠ВАС – кут між діаметром і хордою; ∠ОАС = 60°; ?АОС – рівносторонній. АО = ОС = АС = R.

545.

Вправи 525 574

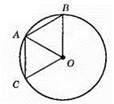
AB = АС = R; ∠САВ – кут між хордами; ∠САВ = ∠САО + ∠АОВ = 60° + 60° = 120°; ?АОС = ?АОВ за трьома сторонами.

Трикутники рівносторонні.

546.

Вправи 525 574

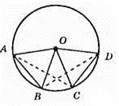
AB = CD; ?AOB = ?COD (за трьома сторонами); АО = ОС; AB = CD; OD = OB. ?АОС = ?BOD; 1) АО = BO; CO = OB; ∠AOC = ∠BOD.

Трикутники рівні за двома сторонами і кутом між ними.

547.

Вправи 525 574

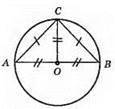
АВ – діаметр кола; АС і СВ – хорди; АС = СВ; ?АОС = ?ВОC; АО = OB; ОС – спільна сторона; АС = ВС; отже, ∠AOC = ∠СОВ – це суміжні рівні кути. ∠COB = 90°.

Відповідь: 90°.

548.

Вправи 525 574

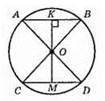
?АОВ = ?COD за трьома сторонами; АО = OD; CO = OB; AB = CD. OK ⊥ AB; OK – відстань від хорди AB до центра кола О.

ОМ ⊥ CD; ОМ – відстань від хорди АВ до центра кола; ?АОК = ?СОМ – прямокутні (за гіпотенузою і гострим кутом). Отже, ОК = ОМ, що і треба довести.

549.

Вправи 525 574

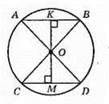
Якщо хорди рівновіддалені від центра кола, то вони рівні.

ОК = ОМ; ?ОКВ = ?ОКА, ОА = OB. ∠A = ∠B; AK = KB; ?OCM = ?ODM; CM = MD; ?AOB = ?COD, AB = CD.

550.

Вправи 525 574

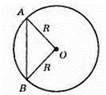
Діаметр є найбільшою хордою кола. AB – довільна хорда; АВ < АО + OB (нерівність трикутника). AB < R + R; AB < d, d – діаметр.

551.

Вправи 525 574

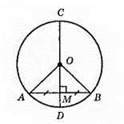
CD ⊥ AB; AM = MB. ?AOM = ?ВОМ (прямокутні). ∠AOD = ∠BOD; ?AOD = ?BOD (за двома сторонами і кутом між ними); АО = OD = OB = R; OD = R; CD – діаметр.

552.

Вправи 525 574

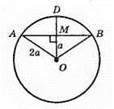
ОМ = а; АО = 2а; АВ – хорда; ОМ – відстань від хорди до центра кола; ОМ ⊥ AB; ∠AMO = 90°; ?АОМ – прямокутний; катет ОМ лежить проти гіпотенузи АО і дорівнює її половині. ∠OAM = 30°;∠AOM = 60°; ∠AOB = ∠AOM + ∠BOM = 60° + 60° = 120°.

553.

Вправи 525 574

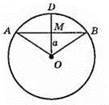
ОМ – відстань від центра О до хорди AB; ОМ ⊥ AB; ОМ = а; АВ = 2а; ?АМО = ?ВМО – прямокутні рівнобедрені трикутники; AM = MO = MB = а; ∠AOM = ∠BOM = 45°; ∠AOВ = ∠AOM + ∠BOM = 45° + 45° = 90°.

554.

Вправи 525 574

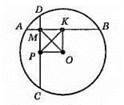
АВ і DC – хорди; AB ⊥ DC, М – точка їх перетину; ОМ – відстань від центра кола до точки їх перетину; ОК – відстань від центра кола до хорди AB, К – середина хорди АВ; ОР – відстань від хорди DC по центра OP ⊥ DC; Р – середина DC. РК – відстань між серединами хорд. ?МОР = ?КРО – прямокутні (рівні за двома катетами) (ОР – спільна сторона; ОК = МР). Отже, МО = РК.

555.

Вправи 525 574

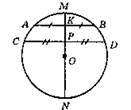
AB і CD – хорди; MN – діаметр. AK = KB; CP = PD. Доведемо, що ці хорди паралельні. AB || CD.

556.

Вправи 525 574

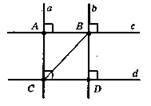
C || d; a ⊥ c; a ⊥ d; b ⊥ c; b ⊥ d. Якщо c || d і a ⊥ c і d, b ⊥ c і d, TO a || b; AC – відстань між паралельними прямими с і d; АС ⊥ с, АС ⊥ d; BD – відстань між паралельними прямими, BD ⊥ с; BD ⊥d; AC = BD.

?ABC = ?DBC – прямокутні; АС = BD, ВС – спільна. З їх рівності: AB = CD. Отже, а і b відтинають від цих прямих рівні відрізки.

557.

Вправи 525 574

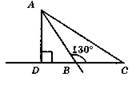
?ABC – тупокутний, AD – висота; AD ⊥ DC; ∠ABC = 130°; ∠ABD – суміжний ∠ABC; ∠ABD = 180° – 130° = 50°; ∠ADB = 90°; AD ⊥ DB; ∠ADB = 90° – 50° = 40°.

Відповідь: 90°; 50°; 40°.

558.

Вправи 525 574

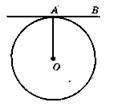
?ОАВ не може мати тупий кут; ОА ⊥ АВ. ∠ОАВ = 90°.

559. а) одну дотичну; б) жодної дотичної не можна провести.

560.

Вправи 525 574

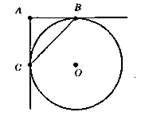
?ABC – рівнобедрений; АВ = АС.

561. а)

Вправи 525 574

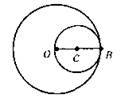
R1 = OB = 8 CM; R2 = CB = 2 CM; d = ОС = 6 см; внутрішній дотик;

Б)

Вправи 525 574

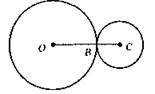
R1 = ВС = 3 см; R2 = OB = 6 см; d = ОС = 9 см; зовнішній дотик.

562.

Вправи 525 574

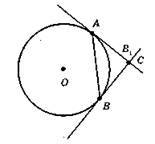
AB – хорда; AB – дотична до кола в точці A; BB1 – дотична до кола в точці В. С – точка перетину дотичних; АС = ВС.

564. а) AB – дотична до кола; ∠АОВ = 20°; ∠ОАВ = 90°; дотична перпендикулярна радіусу проведеному в точку дотику A. ?АОВ – прямокутний. Отже, ∠ОВА = 90° – 20° = 70°.

Вправи 525 574

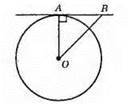
Відповідь: 70°.

Б)

Вправи 525 574

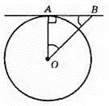
АВ – дотична до кола; ∠AOB = 45°; АВ = 8 см; ∠OAB = 90°; AO ⊥ АВ.

?AOB – прямокутний рівнобедрений; ∠ABO = 90° – 45° = 45°; AО = АВ = 8 см.

Відповідь: 8 см.

565.

Вправи 525 574

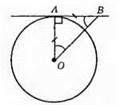
АВ – дотична до кола; А – точка дотику; ОА – радіус, проведений в точку дотику. ОД ⊥ AB; ОАВ = 90°;

ОA = АВ, ?ОАВ – рівнобедрений прямокутний; ∠AOB = ∠ABO – 45°.

Відповідь: 45°; 45°.

566.

Вправи 525 574

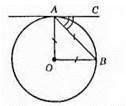
АС – дотична до кола; AB – хорда; АВ = AО; ∠CAB – кут між дотичною і хордою; ?АОВ – рівносторонній. AО = OB = АВ; ∠OAB = 60°; ∠OAC = 90°; OA ⊥ AC, радіус проведений в точку дотику, перпендикулярний до дотичної. ∠BAC = ∠OAC – ∠OAB = 90° – 60° = 30°; ∠BAC = 30°.

Відповідь: 30°.

567.

Вправи 525 574

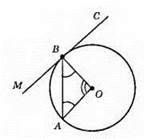
АВ – хорда; ∠AOB = 120°; ?АОВ – рівнобедрений; OB = ОA; отже, ∠OBA = ∠OAB = (180° – 120°) : 2 = 60° : 2 = 30°. ОВ ⊥ ВС; (радіус, проведений в точку дотику, перпендикулярний до дотичної) ∠MBO = 90°; ∠MBA – кут між хордою АВ і дотичною MC; ∠MBA = ∠MBO – ∠ABO = 90° – 30° = 60°.

Відповідь: 60°.

568.

Вправи 525 574

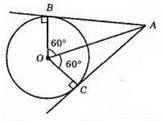
AB – дотична до кола; OB ⊥ AB; ∠OBA = 90°; АС – дотична до кола; ОС ⊥ АС; ∠OCA = 90°; ∠BOC = 150°.

Проведемо ОA; ОA – бісектриса кута ВАС; ∠BAD = ∠CAO; ∠BOC = ∠COA = 120° : 2 = 60°. З? ОВА ∠BAO = 30°. З? ОСА ∠OCA = 30°; ∠BAC = 60°.

Відповідь: 60°.

569.

Вправи 525 574

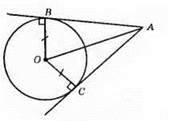
АВ і АС – дотичні до кола, проведені з однієї точки A. ∠BAC = 50°; ?ОАВ = ?ОАС – прямокутні. ОA – спільна сторона, ОВ = ОС; OB ⊥ ВА; ОС ⊥ AC, дотичні, проведені до кола, перпендикулярні до радіусів, проведених в точки дотику. ∠BAO = ∠CAO = 50° : 2 = 25°;

∠BOA = ∠COA = 90° – 25° = 65°;

∠BOC = ∠BOA + ∠COA = 65° + 65° = 130°.

Відповідь: 130°.

570. a)

Вправи 525 574

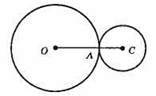
Зовнішній дотик; ОА = 14 см ;АС = 11 см; OC = d – відстань між центрами цих кіл. ОС = ОА + АС = 14 + 11 = 25 (см);

Б)

Вправи 525 574

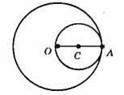
Внутрішній дотик. ОА = 14 см; АС = 11 см; ОС = d – відстань між центрами кіл. ОС = ОА – АС = 14 см – 11 см = 3 см.

Відповідь: 25 см, 3 см.

571.

Вправи 525 574

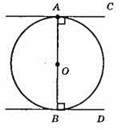
АВ – діаметр, АС і BD – прямі, які дотикаються до кола в кінцях його діаметра АВ. АС ⊥ AB; BD ⊥ АВ (за властивістю дотичних), дві прямі АС і BD перпендикулярні третій прямій АВ, паралельні між собою.

Відповідь: АС || BD.

572.

Вправи 525 574

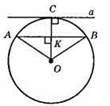
А – дотична до кола в точці С, ОС ⊥ а; АВ – хорда; AK = KB.

?АОК = ?ВОК, ОК – спільна сторона, ОА = OB = R. З рівності трикутників: ∠AKO = ∠OKB, це суміжні кути. Отже, ∠AKO = ∠BKO = 90°, тобто ОС ⊥ АВ; а ⊥ ОС; АВ ⊥ ОС. Отже, а || АВ.

573.

Вправи 525 574

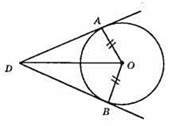
∠ADB – нерозгорнутий кут, AD – дотична до кола. BD – дотична до цього кола; OA ⊥ AD; OB ⊥ BD (властивість дотичної).

?ADO i? BDO – прямокутні, OD – спільна сторона; АО = OB – радіуси кола.

?ADO = ?BDO за гіпотенузою і катетом. Отже, з їхньої рівності маємо: ∠ADO = ∠BDO, DO – бісектриса ∠ADB.

574.

Вправи 525 574

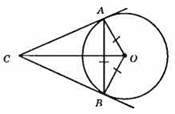
АВ – хорда; АВ = R = АО = OB; АС і ВС – дотичні, С – точка їх перетину. ?AOD – рівносторонній; ∠AOB = 60°.

?АСО = ?ВСО – прямокутні за гіпотенузою ОС і катетами АО і ОВ. АО ⊥ AC; OB ⊥ ВС (за властивістю дотичних). З їхньої рівності ∠ACO = ∠BCO; СО – бісектриса ∠ACB; ?АСО;

∠AOC = 1/2∠AOB = 60° : 2 = 30°; ∠ACO = 90° – 30° = 60°.

Аналогічно ∠OCB = 60°; ∠ACB = ∠ACO + ∠DCO = 60° + 60° = 120°.

Відповідь: 120°.


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Вправи 625-682 625. Геометричним місцем центрів кіл радіуса R, що проходить через дану точку А, є коло із центром в точці А і радіусом R. 626. Геометричним місцем центрів кіл, що дотикаються до сторін даного нерозгорнутого кута, є бісектриса даного кута без його вершини О. ОК – бісектриса. 627. Геометричним місцем точок С, які є вершинами трикутників […]...

  2. Коло і його елементи Розділ 4. Коло і круг. Геометричні побудови § 21. Коло і його елементи 578. PL – хорда, що проходить через центр кола, називається діаметром. 579. 1) 5 х 2 = 10(см); 2) 4,7 х 2 = 9,4 (дм). 580. 1) 8 мм х 2 = 16 мм; 2) 4,8 см х 2 = 7,6 см. […]...

  3. Вправи для повторення розділу 4 Розділ 4. Коло і круг. Геометричні побудови Вправи для повторення розділу 4 До § 21. 756. AB – діаметр, ОС – радіус. AD – хорда. 757. 1) Коло з променем ОК має одну спільну точку. 2) Коло з прямою ОК має дві спільні точки. 758. ?АОВ = ?ВОС за двома сторонами і кутом між ними […]...

  4. Вправи 150-175 150. ∠1 = 90°, ∠2 = ∠1 = 90° – вертикальні кути; ∠3 – суміжний куту ∠1. ∠3 = 180° – 90° = 90°, ∠3 = ∠4 = 90° (вертикальні кути). 151. ∠(ac) = 70°; ∠(ab) = 90°; ∠(bc) = 90° – ∠(ac) = 90° – 70° = 20°. 152. а ⊥ с; ∠(ab) = […]...

  5. Вправи 575-624 575. АВ і АС дотикаються до кола з центром О у точках В і С. ∠CBO = 40°. ?АBО – прямокутний, OB ⊥ AB (OB – радіус, проведений в точку дотику). ?АСО – прямокутний (ОС – радіус, проведений в точку дотику). ∠ABO = 90°; ∠ACO = 90°; ?ВОС – рівнобедрений, OB = ОС; ∠OBC = […]...

  6. Запитання і вправи для повторення § 7 Відповідь: (3; 3), (-1; -2), (1; 0,5). 1012. а) х – 2y = 4; X 0 4 Y -2 0 Б) 4х + у = -4; X 0 -1 Y -4 0 В) 3х – 2y = 6. X 0 2 У -3 0 Відповідь: пара чисел (-2; 3) не являється розв’язком системи рівнянь Х […]...

  7. Вправи 425-474 425. АС – основа; AB = CB; ∠ADC = 150°. ∠CAD = ∠BAD = x; ∠ACD = 2x; x + 2x + 150° = 180°; 3x = 180° – 150°; 3x = 30°; x = 10°; ∠C = ∠A = 20°; ∠B = 180° – (20° + 20°) = 140°. Відповідь: 20°, 20°, 140°. 426. […]...

  8. Вправи 100-49 100. А || b, с || d. 4 точки перетину. 101. 1) Всі чотири прямі перетинають пряму с. 2) Одна пряма паралельна, три перетинають пряму с. 102. 1) m || с; 2) m || b; в) m || а. 103. а || b. Якщо b i c не перетинаються, то через т. М проведено 2 […]...

  9. Вправи для повторення розділу 1 До § 1. 617. Цілі раціональні вирази: Дробові раціональні вирази: А + с 618. 50а кг завезли цукру. Якщо а = 12, то 50а = 50 • 12 = 600 (кг). До § 2. 624. n, n + 1, n + 2 – три послідовні цілі числа; N + (n + 1) + (n + […]...

  10. Властивості кола. Дотична до кола § 3. Паралельні прямі. Сума кутів трикутника § 19. Властивості кола. Дотична до кола Практичні завдання 507. АК = КВ. 508. AB ⊥ CD – дотичні до кола. 509. АС i ВС – дотичні до кола. 510. Таких кіл може бути два. Вправи 511. CD ⊥ AB. ?АОК = ?ВОК (за катетом і гіпотенузою: ОК […]...

  11. Коло. Властивість діаметра, перпендикулярного до хорди Урок № 42 Тема. Коло. Властивість діаметра, перпендикулярного до хорди Мета: перевірити засвоєння учнями основних понять теми “Коло”; вивчити властивість діаметра, перпендикулярного до хорди та обернене твердження; сформувати вміння використовувати набуті знання під час розв’язування задач. Тип уроку: застосування знань, умінь та навичок. Наочність і обладнання: набір демонстраційного креслярського приладдя; таблиця “Властивість діаметра, перпендикулярного до […]...

  12. Вправи 475-524 475. ?ABC – прямокутний; ∠A = 30°; АС = 18 см; ВК – бісектриса, проведена до катета АС; ∠CBK = ∠ABK = ∠CBA : 2 = 60° : 2 = 30°; ∠CBA = 90° – ∠CAB = 90° – 30° = 60°; СК = х, тоді AK = 18 – х. ?АВК – прямокутний; ∠A […]...

  13. Вправи для повторення розділу 3 До § 22. 1116. 1) х + 3 = 2; -5 + 3 = 2; -2 ≠ 2; ні; 2) 2 – х = 7; 2 – (-5) = 7; 7 = 7; -5 є коренем рівняння; 3) х : 5 = 1; -5 : 5 = 1; -1 ≠ 1; ні; 4) 4х = […]...

  14. Взаємне розміщення двох кіл Розділ 4. Коло і круг. Геометричні побудови § 25. Взаємне розміщення двох кіл 656. На рис. 404 кола перетинаються. На рис. 405 кола дотикаються. На рис. 406 кола не мають спільних точок. 657. 1) Кола мають внутрішній дотик. 2) Кола перетинаються. 3) Кола концентричні. 658. 1) Кола мають зовнішній дотик. 2) Кола не перетинаються. 659. […]...

  15. Вправи 375-424 375. ВС – бісектриса ∠ABD; ∠ABD = 80° + 80° = 160°; ∠BAC + ∠ABD = 20° + 160° = 180°; ∠BAC і ∠ABD – внутрішні односторонні кути при прямих АС і BD та січній АВ. Отже, BD || АС. 376. ∠A = 70°, ∠B = 40°, BE – бісектриса ∠ABD; ∠DBE = ∠ABE = […]...

  16. Вправи для повторення до розділу 2 Розділ 2. Взаємне розміщення прямих па площині Вправи для повторення до розділу 2 До § 5. 226. На рис. 184 суміжні кути ∠2 і ∠3. на рис. 185 суміжні кути ∠1 і ∠4 та ∠2 i ∠3. На рис. 186 суміжні кути ∠1 і ∠2 та ∠3 i ∠4. 227. 1) Так, можна. Треба побудувати […]...

  17. Дотична до кола, її властивості Розділ 4. Коло і круг. Геометричні побудови § 22. Дотична до кола, її властивості 607. Проведемо радіус ОР, а потім за допомогою косинця побудуємо пряму m, перпендикулярну до радіуса. За теоремою 2 пряма m є дотичною до кола. 608. Проведемо радіус ОМ, а потім за допомогою косинця побудуємо пряму n, перпендикулярну до радіуса. За теоремою […]...

  18. Геометричні побудови Урок № 52 Тема. Геометричні побудови Мета: продіагностувати рівень засвоєння учнями знань та вмінь, передбачений програмою під час вивчення теми “Геометричні побудови”. Тип уроку: перевірка і корекція знань, умінь та навичок. ХІД УРОКУ І. Організаційний момент ІІ. Перевірка домашнього завдання Зібрати зошити з домашньою контрольною роботою ІІІ. Умова контрольної роботи Варіант 1 Початковий рівень 1. […]...

  19. Вправи 275-324 275. Кут В. а) ВА = ВС, ?АВС – рівнобедрений, у нього дві сторони рівні; Б) ∠A = ∠C. 276. ∠A = 60°; AD – бісектриса кута А. BC ⊥ AD; AB = AC; ∠B = ∠C. 277. AB = ВС; АС – основа. Нехай АВ = ВС = х м, тоді АС = (х […]...

  20. Вправи на визначення відмінка прикметника у реченні за відмінком іменника. Контрольна робота: списування. (Вправи 179-181) Тема. Вправи на визначення відмінка прикметника у реченні за відмінком іменника. Контрольна робота: списування. (Вправи 179-181). Мета. Вчити учнів за допомогою відмінкової форми іменників визначати відмінок прикметників у реченнях, виховувати шанобливе ставлення до Батьківщини. Обладнання: вірші, прислів’я про Батьківщину, запис “Пісні про рушник” на сл. А. Малишка, індивідуальні картки з текстом пісні. Хід уроку I. […]...

  21. Вправи на вживання різних відмінкових форм прикметників у множині. (Вправи 210-212) Тема. Вправи на вживання різних відмінкових форм прикметників у множині. (Вправи 210-212). Мета. Вчити школярів правильно вимовляти і вживати на письмі закінчення прикметників, орієнтуючись на кінцевий приголосний основи. Обладнання: експозиція дитячих квітів-розмальовок, таблиця “Почуття”, таблиця-ватман “Словничок”. Хід уроку I. Організація класу. II. Перевірка домашнього завдання. 1. Вправа “Крісло автора”. Діти зачитують твори про мамині (бабусині) […]...

  22. Тренувальні вправи на використання прикметників у мовленні. Практичні словотворчі вправи. Усний опис зимового пейзажу Урок 65 Тема. Тренувальні вправи на використання прикметників у мовленні. Практичні словотворчі вправи. Усний опис зимового пейзажу Мета: вдосконалювати вміння рід, число і відмінок у сполученні з іменником, вміння добирати прикметники-синоніми, повторити правило перевірки ненаголошеного голосного у корені слова; розвивати словотворчі вміння дітей, усне мовлення; виховувати любов до природи. Обладнання: картинки зимової природи, словники синонімів, […]...

  23. Вправи на визначення роду і числа прикметників за іменниками. (Вправи 168-170) Тема. Вправи на визначення роду і числа прикметників за іменниками. (Вправи 168-170). Мета. Виявити істотну відмінність між прикметниками та іменниками як частинами мови: кожний прикметник залежно від іменника може змінюватись не тільки за числами і відмінками, а й за родами; вчити розпізнавати рід прикметників за родом іменників та формальними ознаками – родовими закінченнями. Обладнання: таблиця […]...

  24. Коло і круг Розділ 1. Найпростіші геометричні фігури та їх властивості § 15. Коло і круг 588. 1) Хордами є відрізки: KB, NC, KN, CB, LD. 2) Діаметрами є відрізки: LD, NC, КВ. 3) Радіусами кола є відрізки: OL, OK, ОС, OD, OB, ON. 589. Дотичні до кола: АС, CB, AB. ON ⊥ AC, ОМ ⊥ CB, OK […]...

  25. Коло Геометрія Основні властивості найпростіших геометричних фігур Коло Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки. Ця точка називається Цент­ром кола. Відстань від точок кола до його центра називається Радіусом кола. Радіусом також називається будь-який відрізок, що сполучає точку кола з його центром. Відрізок, що сполучає дві точки кола, називається Хордою. […]...

  26. Вправи на доцільне використання прикметників у мовленні. Спостереження за формами прикметників найвищого ступеня (без терміна, практично). (Вправи 163-167) Тема. Вправи на доцільне використання прикметників у мовленні. Спостереження за формами прикметників найвищого ступеня (без терміна, практично). (Вправи 163-167). Мета. Вчити школярів добирати прикметники для найточнішого вираження думки: показати роль прикметників найвищого ступеня у мовленні. Обладнання: книги В. Нестайка “Казкові пригоди і таємниці”, прислів’я, мовний матеріал. Хід уроку I. Організація класу. II. Перевірка домашнього завдання. […]...

  27. Вправи 176-224 176. Якщо три точки лежать на прямій, вони не можуть бути вершинами трикутника. 177. А) Кути прилеглі до сторони МР: ∠KMP і ∠KPM; Б) ∠KMP – протилежний стороні KP; В) сторона протилежна куту K – МР; В) сторони прилеглі до кута Р – KP і РМ. 178. Якщо два трикутники рівні, то їх периметри рівні. […]...

  28. Вправи 225-273 225. L ⊥ AB; X – точка прямої l; О – середина AB. ?АОХ = ?BOX (за першою ознакою рівності трикутників). 1) АО = OB; 2) ∠3 = ∠4 = 90°; 3) ОХ – спільна сторона. З цього випливає АХ = ВХ, отже, точка X рівновіддалена від кінців відрізка А і В. 226. Три прямі […]...

  29. Вправи 325-374 325. ?ABC; AB = AC; ?A1B1C1; A1B1 = A1C1; ∠B = ∠B1; BK = B1K1. ∠AKB = ∠CKB = ∠A1K1B1 = ∠C1K1B1 = 90°. ?АВK = ?A1B1K1. 1) BK = В1K1; 2) ∠1 = ∠2; 3) ∠3 = ∠4, отже, AB =A1B1. ?АВС = ?А1В1С1. AB = A1B1; BC = В1С1; ∠B = ∠B1. 326. […]...

  30. Задачі за готовими рисунками ДОДАТКИ Задачі за готовими рисунками 1 О – центр кола. Знайдіть АС 2 NB – діаметр, NB = 10, ОК = 4. Знайдіть АВ 3 О – центр кола. Знайдіть МО 4 Знайдіть АЕ 5 Знайдіть ВС 6 О – центр кола, АВ дотична, ОА = 25. Знайдіть АВ 7 О – центр кола. АВ […]...

  31. Властивості прямокутного трикутника § 3. Паралельні прямі. Сума кутів трикутника § 17. Властивості прямокутного трикутника 457. Найбільший катет трикутника дорівнює 24 см. 458. ?DEF – прямокутний, ∠F = 90°, ∠D = 30°, DE = 18 см. Відповідь: 9 см. 459. ?KCM – прямокутний, ∠M = 90°, ∠C = 60°, MC = 7 см. ∠MKC = 90° – 60° […]...

  32. Описане та вписане коло трикутника § 3. Паралельні прямі. Сума кутів трикутника § 20. Описане та вписане коло трикутника 540. 1) Різносторонній гострокутний трикутник. 2) Прямокутний трикутник. 3) Тупокутний трикутник. 541. 1) Рівнобедрений гострокутний трикутник. 2) Рівнобедрений тупокутний трикутник. 542. 543. 544. Вправи 545. Медіана BD рівнобедреного трикутника ABC є в той же час і серединним перпендикуляром до сторони АС […]...

  33. Повторення вивченого за рік. (Вправи 351-358). Урок розвитку мовлення. Повторення вивченого за рік. (Вправи 359-362). Контрольна робота: диктант Тема. Повторення вивченого за рік. (Вправи 351-358). УРОК 110 Урок розвитку мовлення УРОК 111 Тема. Повторення вивченого за рік. (Вправи 359 362). УРОК 112 Тема. Контрольна робота: диктант. Мета. Перевірити вміння правильно писати слова на вивчені орфограми та словникові слова, визначені для запам’ятовування; ставити розділові знаки відповідно до опрацьованих правил пунктуації. Хід уроку I. Організація […]...

  34. ЗАДАЧІ ТА ВПРАВИ МЕХАНІКА РОЗДІЛ 2. МЕХАНІЧНИЙ РУХ ЗАДАЧІ ТА ВПРАВИ Рівень А 116. На тіло завжди діє сила тяжіння однаково у будь-якому місці на Землі, якщо вважати, що g = 9,81 м/с2. (9,81 Н/кг) 117. Земля притягує до себе предмет, який випущено з рук. На нього діє сила тяжіння. 118. Сила тяжіння спричиняє падіння на Землю граду, […]...

  35. Пропорційність відрізків хорд і січних кола Геометрія Кути, пов’язані з колом Пропорційність відрізків хорд і січних кола Теорема 1. Якщо хорди AB і CD кола перетинаються в точці S, то (рисунок 1). Теорема 2. Якщо з точки P до кола проведені дві січні, що перетинають коло відповідно в точках A, B, C, D, то (рисунок 2). Тобто добуток січної, проведеної до […]...

  36. Вправи 1-49 1. А є ВС; В є АС. 2. А є с; В ∉ с. AB і с перетинаються в точці А. 3. Ці прямі мають тільки одну спільну точку А. 4. Точки В і С лежать по один бік від точки А. 5. а) Точка М лежить між L i N; Б) L і М […]...

  37. Вправи для повторення розділу 2 До § 19. 819. Площа квадрата залежить від довжини його сторони. Площа квадрата є функцією від довжини сторони квадрата: S = х2. Якщо сторона квадрата а, то площа S = а2. 820. X -4 -2 0 2 4 Y 2/7 0 -2/3 -4 6 G 8/5 -6/5 -4/5 -2/5 0 821. у = 48 – […]...

  38. ЗАДАЧІ І ВПРАВИ МЕХАНІКА РОЗДІЛ 3. МЕХАНІЧНА РОБОТА ТА ЕНЕРГІЯ ЗАДАЧІ ТА ВПРАВИ Рівень А 363. Чим менша довжина сірника, тим менше плече сили. Отже, треба прикладати велику силу, щоб розламати сірник. Легше розламати сірник посередині, тому що більше плече сили. 364. Картон потрібно розташовувати ближче до середини. (Зменшуючи плече, ми збільшимо силу, що діє на картон). 365. […]...

  39. Вправи на сумісні дії. Задачі на зустрічний рух (№№ 715-722) Тема. Вправи на сумісні дії. Задачі на зустрічний рух (№№ 715-722). Мета. Закріплювати вміння учнів знаходити значення виразів на сумісні дії, розв’язувати рівняння; вчити учнів розв’язувати задачі на зустрічний рух. Обладнання. Таблиці для усних обчислень; схеми задач; план розв’язування задачі. Зміст уроку І. Контроль, корекція і закріплення знань. 1. Перевірка домашнього завдання. А) Пояснити розв’язання […]...

  40. Взаємне розміщення двох кіл на площині – СТЕРЕОМЕТРІЯ Формули й таблиці МАТЕМАТИКА СТЕРЕОМЕТРІЯ Взаємне розміщення двох кіл на площині D = О1, O2 – відстань між центрами кіл. R, r – радіуси кіл. D < R – r – кола не мають спільних точок. D = R – r – внутрішній дотик кіл, кола мають одну спільну точку. R – r < d […]...

Ви зараз читаєте: Вправи 525-574
«
»