ЗАДАЧІ НА ПОБУДОВУ
РОЗДІЛ 4 КОЛО І КРУГ. ГЕОМЕТРИЧНІ ПОБУДОВИ
& 21. ЗАДАЧІ НА ПОБУДОВУ
З геометричними побудовами мають справу різні фахівці. Геометричні побудови виконують креслярі, архітектори, конструктори, топографи, геодезисти, штурмани. Геометричні фігури також будують: слюсар – на жерсті, столяр – на дошці, кравець – на тканині, садівник – на землі.
У задачі на побудову вимагається побудувати геометричну фігуру, яка повинна задовольняти певні умови. У геометри побудови виконують найчастіше за допомогою лінійки і циркуля. Домовимось,
Складніші задачі на побудову часто розв’язують методом геометрии них місць. Нехай, наприклад, у задачі треба знайти точку X, що задовольняє дві умови. Якщо першу умову задовольняють точки фігури ІГ, а другу – точки фігури Р, то точка X має належати кожній із цих фігур. Тобто X – точка перетину фігур К і Р.
ЗАДАЧА 1
Побудуйте прямокутний трикутник за даним катетом а і гіпотенузою с (мал. 253).
РОЗВ’ЯЗАННЯ. Перший спосіб. Будуємо прямий кут АСВ. На його стороні відкладаємо
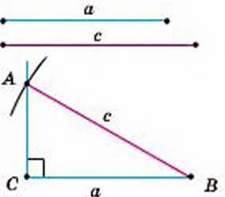
Мал. 253
Другий спосіб (мал. 254). Відкладаємо відрізок АВ = с і проводимо коло діаметра АВ – ГМТ, з яких АВ видно під прямим кутом. Далі будуємо коло радіуса а з центром В – ГМТ, віддалених від точки В на відстань а. Якщо два ГМТ перетинаються в точці С, то трикутник ABC – той, який вимагалось побудувати. Два розглянуті кола можуть перетинатися ще в одній точці – C1. Але трикутники ABC і ABC1, рівні, тому вважаються одним розв’язком.
Складові частини розв’язання задачі на побудову – аналіз, побудова, доведення і дослідження. В аналізі шукається спосіб розв’язування задачі, у побудові – виконується побудова, у доведенні – обгрунтовується правильність виконаної побудови, у дослідженні – з’ясовується, скільки розв’язків має задача.
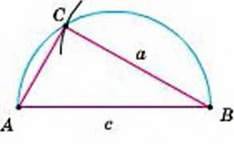
Мал. 254
ЗАДАЧА 2
Побудуйте трикутник за даною стороною, прилеглим до неї кутом і сумою двох інших сторін (мал. 256).
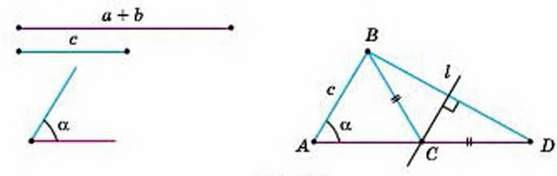
Мал. 255
РОЗВ’ЯЗАННЯ.
Аналіз. Припустимо, що потрібний трикутник ABC побудовано. Його сторона с і ∠A = а – дані. Дано також відрізок, який дорівнює сумі сторін а і b. За даними відрізками с і а + b та кутом А між ними можна побудувати∠ABD. Вершиною С шуканого трикутника буде така точка відрізка AD, для якої CD = СВ. Отже, точка С повинна лежати і на серединному перпендикулярі відрізка BD.
П о б у д о в а. За двома даними відрізками і кутом між ними будуємо ∆АВD, після чого проводимо серединний перпендикуляр І до відрізка BD. Нехай пряма l перетинає відрізок AD в точці С. Проводимо відрізок СВ. Трикутник ABC – той, який вимагалось побудувати.
Доведення. У трикутнику АВС АВ = с і ∠A = а за побудовою. АС + СВ = АС + CD = а + b. Отже, ДАВС задовольняє всі умови задачі.
Д о с л і д ж е н н я. Задача мас розв’язок тільки за умови, що а + b > c.
Зверніть увагу! Якщо задача нескладна і спосіб її розв’язування відомий, аналіз можна не описувати. А в розв’язанні не обов’язково виділяти аналіз, побудову, доведення і дослідження.
Для допитливих
У математиці найчастіше мають справу із задачами: на обчислення, на доведення, на побудову, на перетворення і на дослідження. Геометричними задачами на побудову активно цікавилися античні геометри. Допускаючи тільки класичні побудови (які виконуються лише лінійкою і циркулем), вони досліджували, які з побудов можна виконати, а які не можна. Зокрема, з’ясовували:
1) чи можна будь-який кут поділити на три рівні частини;
2) чи можна побудувати квадрат, площа якого дорівнювала б площі даного круга;
3) чи можна побудувати ребро такого куба, об’єм якого був би у 2 рази більший за об’єм даного куба.
Багато століть видатні геометри намагалися розв’язати ці задачі і не змогли. Ці три класичні задачі давнини дістали спеціальні назви: 1) трисекція кута; 2) квадратура круга; 3) подвоєння куба. Останню задачу називають ще делоською задачею, пов’язуючи її з давньогрецькою легендою, за якою оракул бога Аполлона погодився врятувати жителів острова Делос від чуми, якщо кубічний жертовник у делоському храмі замінять жертовником такої самої форми, але вдвічі більшого об’єму. І майже через 2000 років учені переконалися. що жодну з цих трьох задач за допомогою лише лінійки і циркуля розв’язати не можна.
Тепер фахівці, яким доводиться виконувати геометричні побудови, користуються не тільки лінійкою і циркулем. Багато побудов виконують на комп’ютері за допомогою спеціального програмного забезпечення.
З погляду класичних методів такі побудови наближені. Але для практичних потреб точність, яку забезпечують наближені методи, цілком достатня.
Запитання і завдання для самоконтролю
1. Якими інструментами найчастіше виконують побудови в геометрії?
2. Назвіть складові частини розв’язання задачі на побудову.
3. Що таке трисекція кута, квадратура круга, подвоєння куба?
Виконаємо разом
1. Знайдіть центр даного кола.
Позначимо на даному колі три довільні точки А, В і С (мал. 256).
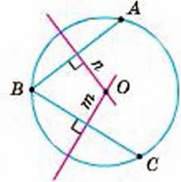
Мал. 256
Проведемо хорди АВ, ВС і побудуємо їх серединні перпендикуляри n і m.
Точка О, у якій перегинаються прямі n і m, – центр даного кола.
Адже ОА = ОВ = ОС.
2. Через дану точку проведіть дотичну до даного кола.
Якщо дана точка А лежить на колі з центром О (мал. 257, а), проводимо промінь ОА, а потім – пряму АК, перпендикулярну до ОА. Пряма АК – дотична, яку треба було побудувати.
Якщо точка А лежить поза даним колом я центром О (мал. 267, б), то на діаметрі ОА описуємо коло. Воно перетнеться з даним колом у двох точках К і Р. Прямі АК і АР – шукані дотичні, бо АК ⏊OK і АР ⏊ ОР. (Із точок Кі Р допоміжного кола його діаметр ОА видно під прямими кутами АК О і АРО.) У цьому випадку задача має два розв’язки.
Якщо точка А лежить усередині кола, задача не має розв’язку, бо дотичну провести не можна.
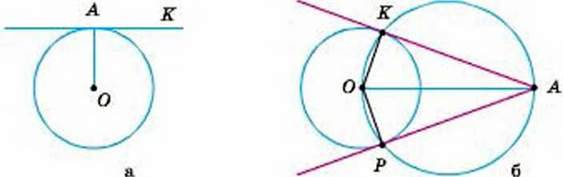
Мал. 257
ЗАДАЧІ I ВПРАВИ
Виконайте усно
А
618. Побудуйте рівнобедрений трикутник за основою і висотою, проведеною до основи.
619. Побудуйте прямокутний трикутник:
1) за гіпотенузою і гострим кутом;
2) за гіпотенузою і катетом;
3) за катетом і прилеглим до нього гострим кутом;
4) за катетом і протилежним кутом.
620. Побудуйте трикутник за двома сторонами і медіаною” проведеною до однієї з них.
621. Побудуйте трикутник за двома сторонами і висотою, проведеною: 1) до однієї з низе; 2) до третьої сторони.
622. Побудуйте рівнобедрений прямокутний трикутник:
1) за даним катетом;
2) за гіпотенузою:
3) за медіаною, проведеною до гіпотенузи.
623. Знайдіть на даній прямій точку, що лежить на даній відстані від іншої даної прямої.
624. Знайдіть на даній прямій тонку, що лежить на однакових відстанях від двох даних точок.
625. Побудуйте коло, що дотикається до сторін даного кута, причому до однієї з них – у даній точці.
626. Побудуйте прямокутний трикутник за катетом і радіусом описаного кола.
627. Побудуйте трикутник за двома сторонами і радіусом описаного капа.
628. Побудуйте трикутник за стороною, медіаною, проведеною до цієї сторони, і радіусом описаного кола.
629. Побудуйте рівнобедрений трикутник за радіусом описаного кола і основою.
Б
630. Побудуйте прямокутний трикутник за радіусом описаного кола і гострим кутом.
631. Дано паралельні прямі a, b і точку А між ними (мал. 268). Побудуйте коло, що проходить через точку А і дотикається до прямих а і b.

Мал. 258
632. Побудуйте рівносторонній трикутник за радіусом описаного кола.
633. Як побудувати спільну дотичну:
А) до двох кіл, радіуси яких однакові;
Б) до двох кіл, радіуси яких різні?
634. Побудуйте прямокутний трикутник за гіпотенузою і висотою, проведеною з вершини прямого кута.
635. Побудуйте прямокутний трикутник за катетом і сумою двох інших сторін.
636. Побудуйте прямокутний трикутник за катетом і радіусом вписаного кола.
637. Побудуйте рівнобедреник трикутник за основою і радіусом вписаного кола.
638. Побудуйте геометричне місце точок, з яких даний відрізок а видно під кутом 90°.
639. Побудуйте прямокутний трикутник за даними медіаною і висотою, проведеними до гіпотенузи.
640. Покажіть, як можна наближено поділити:
A) коло на 7 рівних частин;
Б) довільний кут на 3 рівні частини;
В) довільну дугу кола на б рівних частин.
Практична завдання
641. Побудуйте коло радіуса 5 см і впишіть у нього рівносторонній трикутник ABC. За допомогою циркуля і лінійки поділіть кожну з дуг АВ, ВС і АС навпіл точками К, L і М відповідно. З’єднайте послідовно точки, щоб утворився шестикутник AKBLCM. Виміряйте його сторони і порівняйте з радіусом кола.
ВПРАВИ ДЛЯ ПОВТОРЕННЯ
642. Висота рівностороннього трикутника дорівнює h, а радіуси вписаного і описаного кола r і R відповідно. Доведіть, що r + R = h.
643. З вершини В трикутника ABC проведено висоту ВН і медіану ВМ.
AH = 3 см, АС = 10 см. Знайдіть НМ, якщо:
1) ∠A – гострий; 2) ∠A – тупий.
644. Доведіть, що бісектриси двох вертикальних кутів лежать на одній прямій.
645. Точку, рівновіддалену від усіх вершин рівностороннього трикутника, сполучили з його вершинами (мал. 259). Доведіть, що всі три утворені трикутники рівні. Чи буде правильніш твердження задачі, якщо точка О лежить поза площиною трикутника?
646. Радіуси двох кіл – 3 см і 5 см. Чи перетинаються кола, якщо відстань між їх центрами дорівнює: а) 1 см; б) 3 см; в) 8 см; г) 10 см?
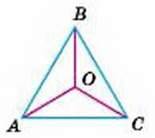
Мал. 259
Геометрія навколо нас

ЗАДАЧІ ЗА ГОТОВИМИ МАЛЮНКАМИ
А
1
АС, DD – діаметри.
Довести:
АВ || CD.
2
R1 : r2 = 2 : 3,O1O2 = 15.
R1, r1
3
OB = 2,5OА.
АВ= 18.
AO, ОВ
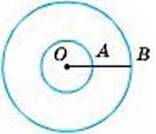
4
СК= 2,КВ = 7,
P∆АВС = 24
АВ
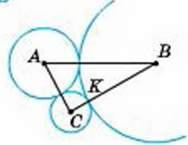
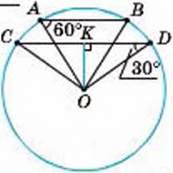
Б
1
АВ = 8, ∠A = 60,
∠D = 30°.
ОК
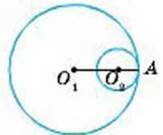
2
О1А = 3О2А, О1О2 = 10.
О1А, О2 А
3
ВС – спільна дотична.
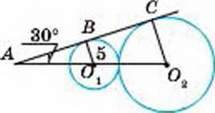
4
В, Р, С – точки дотику,
Р∆АМН
ОВ
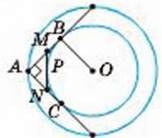
ЗАДАЧІ ЗА ГОТОВИМИ МАЛЮНКАМИ
А
1
∠A = 60°, ОВ = 5.
АК
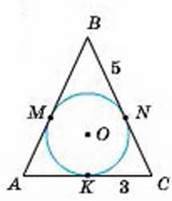
2
АВ = ВС,
BN = 5,
КС = 3.
Р∆АВС
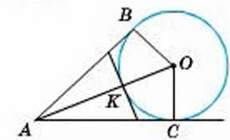
3
АВ = 25, АС = 7,
ВС = 24.
R
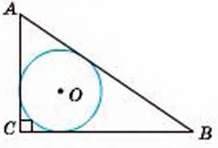
4
АС = 10.
АО
Б
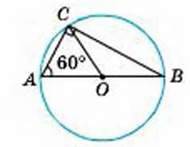
1
∠BAC = 60°, ОВ = 6.
AK
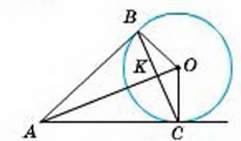
2
MB = З, АM = 5,
P∆ABC
ВС, АС
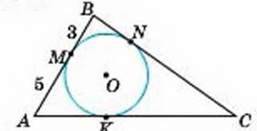
3
AN : NB = 3 : 2, ОN = 4,
P∆ABC = 48
АВ, ВС, АС
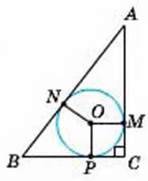
4
ОА = 7, АВ = 120°,
АВ = ВС.
AB
Самостійна робота 5
Варіант 1
1. Знайдіть довжину чверті кола радіуса 10 мм.
2. Користуючись циркулем і лінійкою з поділками, побудуйте прямокутний трикутник за гіпотенузою і катетом, довжини яких дорівнюють 8 мм і 6 см. Опишіть навколо цього трикутника коло.
3. Сформулюйте означення серединного перпендикуляра до відрізка.
Варіант 2
1. Знайдіть площу чверті круга радіуса 20 см.
2. Користуючись циркулем і лінійкою з поділками, побудуйте прямокутний трикутник за гіпотенузою і катетом, довжини яких дорівнюють 8 см і 4 см. Опишіть навколо цього трикутника коло.
3. Сформулюйте означення дотичної до кола.
Варіант З
1. Радіус вписаного в прямокутний трикутник кола дорівнює 5 см. На скільки сума катетів більша за гіпотенузу?
2. Користуючись циркулем і лінійкою з поділками, побудуйте рівнобедрений трикутник за основою і бічною стороною, довжини яких дорівнюють 8 см і 5 см. Опишіть навколо цього трикутника, коло.
3. Сформулюйте означення кола, описаного навколо трикутника.
Варіант 4
1. Знайдіть гіпотенузу прямокутного трикутника, якщо радіус кола, описаного навколо нього, дорівнює r.
2. Користуючись циркулем і лінійкою з поділками, побудуйте трикутник за трьома сторонами, довжини яких дорівнюють 3 см, 3,5 см і 4 см. Опишіть навколо цього трикутника коло.
3. Сформулюйте означення кола, вписаного в трикутник.
Тестові завдання 5
1. Діаметр кола дорівнює 6 cм. Довжина кола дорівнює: | А) 6п см; б) 3п см; В) 9п см; г) 36п см. |
2. 2. Центр кола, вписаного в трикутник, лежить у точці перетину: | А) бісектрис; Б) медіан; В) висот; Г) серединних перпендикулярів. |
3. 3. Центр кола, описаного навколо прямокутного трикутника” лежить на середині: | А) медіани; Б) катета; В) гіпотенузи; Г) бісектриси. |
4. 4. Гіпотенуза прямокутного трикутника дорівнює 12 см. Знайдіть радіус описаного кола. | А) 10 см; б) 6 см; В) 4 см; г) 12 см. |
5. 5. Сторони прямокутного трикутника дорівнюють 6 см, 8 см і 10 см. Знайдіть радіус вписаного кола. | А) 4 см; б) 8 см; В) 12 см; г) 2 см. |
6. 6. Із точки А до кола проведено дотичні АВ і АС (В і С – точки дотику). Яке з тверджень правильне? | А )АВ = АС; б )АВ < АС; В) АВ > АС; г) АВ ≠ АС. |
7. 7. Кола радіусів 3 см і 7 см дотикаються зовні. Знайдіть відстань між центрами цих кіл. | А) 2 см; б) 4 см; В) 10 см; г) 5 см. |
8. 8. Знайдіть ширину кільця, утвореного концентричними колами радіусів 3 см і 5 см. | А) 8 см; б) 2 см; В) 4 см; г) 4 п см. |
9. 9. 3 точки А до кола з центром О проведено дотичну АВ (В – точка дотику). Тоді ∠AВО: | А) гострий; Б) прямий; В) тупий; Г) розгорнутий. |
10. Геометричним місцем точок площини, рівновіддалених від даної точки, є: | А) коло; б) квадрат; В) круг; г) куб. |
ТИПОВІ ЗАДАЧІ ДЛЯ КОНТРОЛЬНОЇ РОБОТИ
1. Накресліть коло діаметра б см. Чому дорівнює його радіус?
2. Чи мають спільні точки дна кола, якщо їх радіуси дорівнюють 2 см і 5 см, а відстань між їх центрами становить 8 см?
3. Накресліть гострий кут і побудуйте його бісектрису.
4. Навколо трикутника ABC а кутами ∠A = 30° і ∠B = 60° описано коло. Знайдіть його радіус, якщо АВ = 10 см.
5. Кут між двома радіусами кола дорівнює 130°. Знайдіть кут між дотичними, проведеними через кінці цих радіусів.
6. Два кола мають зовнішній дотик, а відстань між їх центрами дорівнює 16 см. Знайдіть радіуси цих кіл, якщо вони відносяться як 3 : 5.
7. З точки А до кола з центром О проведемо дотичні AM і AN (М і N – точки дотику). К – точка перетину відрізків MN і АО. Знайдіть АК і КО, якщо ОМ = 8 см і ∠MON = 120°.
8. Побудуйте прямокутний трикутник за радіусом описаного кола r = 3 см і гострим кутом, що дорівнює 45°.
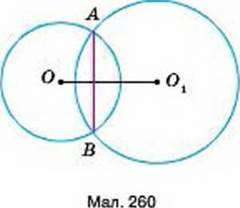
9. Доведіть, що коли два кола з центрами О і O1 перетинаються в точках А і В, то АВ і ОО1 (мал. 260).
10. Побудуйте рівнобедрений трикутник за бічною стороною (6 см) і проведеною до неї медіаною (б см).
ГОЛОВНЕ В РОЗДІЛІ 4
Коло – фігура, що складається з усіх точок площини, рівновіддалених від даної точки. Круг – частина площини, обмежена колом. Пряма, яка має з колом тільки одну спільну точку і лежить у площині кола, називається дотичною до кола. Хорди кола – відрізок, кінці якого належать даному колу. Найбільша хорда кола – його діаметр.
Діаметр кола, проведений через середину хорди. відмінної від діаметра, перпендикулярний до неї.
Дотична до кола перпендикулярна до радіуса, проведеного в точку
Дотику.
Точки дотику кола до сторін кута рівновіддалені від ного вершини.
Коло, яке проходить через усі вершини трикутника, називають описаним навколо даного трикутника. Коло, яке дотикається до всіх сторін трикутника, – вписане в даний трикутник. Навколо будь-якого трикутника можна описати коло і в будь-який трикутник можна вписати коло.
Центром кола, вписаного в трикутник, є точка перетину бісектрис трикутника.
Центр кола, описаного навколо трикутника, – точка перетину серединних перпендикулярів сторін даного трикутника.
Серединний перпендикуляр до відрізки – пряма, яка перпендикулярна до даного відрізка і проходить через його середину.
Діаметр кола, описаного навколо прямокутного трикутника, дорівнює його гіпотенузі.
Діаметр кола, вписаного в прямокутний трикутник з катетами а і b і гіпотенузою с, дорівнює а + b – с.
Користуючись тільки лінійкою і циркулем, можна: будувати трикутник за трьома даними сторонами і кут, що дорівнює даному; проводити бісектрису кута; ділити навпіл відрізок; будувати пряму, перпендикулярну до даної прямої, тощо.
Один із найважливіших видів геометричних задач – задачі на побудову. Найчастіше їх розв’язують методом геометричних місць.
Геометричне місце точок – це множина точок, які мають певну’ властивість.
Геометричним місцем точок, рівновіддалених від кінців відрізка, є серединний перпендикуляр цього відрізка. Йдеться про фігури однієї площини.
Геометричне місце точок кута, рівновіддалених від його сторін, – бісектриса цього кута.
До &1
647. Користуючись малюнком 261, укажіть:
А) у якій точці перетинаються прямі а і b;
Б) які точки належать прямій а, прямій b;
В) які точки не належать жодній з прямих а і b;
Г) чи належить точка О прямій а? прямій b.
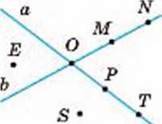
Мал. 261
648. Точки А, В і С лежать на прямій а. Точки М, N і К не належать прямій а. Зобразіть це на малюнку.
649. М ∈ а, N ∉ а, К ∉ а, причому N і K лежать по різні боки від прямої а. Зобразіть це на малюнку.
650. Hа прямій а дано точки А і В. Зобразіть точки М і N так, щоб точка М лежала між точками А і B, а точка В – між точками М і N.
651. Зобразіть на малюнку:
А) три прямі, які перетинаються в одній точці;
Б) три прямі, дві з яких не перетинаються;
В) три прямі, які попарно перетинаються у трьох точках.
На скільки частин у кожному випадку прямі розбивають площину?
До &2
652. М – внутрішня точка відрізка АВ. Знайдіть довжину відрізка АВ, якщо ВМ = 5 см і:
А) відрізок АМ на 2 см більший за відрізок ВМ;
Б) відрізок AM у 3 рази більший за відрізок ВМ;
В) AM : ВМ = 3 : 2;
Г) АВ = З АМ.
653. Точки А, В і С лежать на одній прямій, причому відрізок АВ у 3 рази менший від відрізка ВС. Знайдіть відрізки АВ і ВС, якщо АС = 8 см. Скільки розв’язків має задача?
654. Точки А, В, С і D лежать на одній прямій, причому АВ = 2 см, ВС = 4 см, CD = 7 см. Чому дорівнює відрізок АВ? Розгляньте всі можливі випадки.
655. Точка С – середина відрізка АВ, D – середина відрізка АС. Знайдіть відношення AD : АВ; AD : ВС; ВС : ВС.
656. Точка С – середина відрізка АВ, В – середина відрізка СВ. Знайдіть довжину відрізка АВ, якщо:
А) СВ = 2 см; б) ВС – СВ = 3 см; в) АС – ВС = 4 см.
657. М – внутрішня точка відрізка АВ. К і Р – середини відрізків AM і MB відповідно. Знайдіть довжину відрізка KP, якщо АВ = 10 см.
658. Точка М – середина відрізка АВ, а точка К ділить відрізок AM у відношенні АК : КМ =1 : 2. Знайдіть довжину відрізка МК якщо:
А) АВ = 12 см; б) ВМ = 9 см; в) MB – АК = 10 см.
659. На прямій а лежать точки А, В і С, причому АВ = 12 см, АС + СВ = = 15 см. Знайдіть довжини відрізків АС і ВС.
660. Точки А, В і С лежать на одній прямій. ВС = 6 см, АВ + АС =10 см. Знайдіть довжини відрізків АВ і АС.
661. АВ = 10 см. Точка С – середина відрізка АВ. Па прямій АВ знайдіть усі точки В, такі що: DA + DB + DC =12 см. Зобразіть ці точки на малюнку.
662. Точки А і В лежать по різні боки від прямої а, точка М ∈ a. AМ = 10 см, ВМ =16 см, АВ = 23 см. Чи є точка М точкою перетину прямих АВ і а?
663. Є лінійка з поділками 0, 3 см і 7 см. Як за допомогою цієї лінійки побудувати відрізок завдовжки 4 см; 11 см?
До &3
661. ОМ – внутрішній промінь кута АОВ. Знайдіть ∠АОМ і ∠ВОМ, якщо ∠ОВ = 80° і:
А) ∠АОМ у 3 рази менший від ∠МОВ;
Б) ∠BOM на 20° більший за ∠АОМ;
В) ∠АОМ : ∠ВОМ =1 : 3;
Г) ∠ВОМ = ∠АОМ.
665. Прямий кут розбили двома внутрішніми променями на кути, один із яких на 20° більший за другий і на 20° менший від третього. Знайдіть ці кути.
666. ОС – бісектриса кута АОВ. ОМ – бісектриса кута АОС. Знайдіть ∠AOB, якщо ∠MOC = 20°.
667. ∠AOB = 80°, ∠BOC = 20°, ОМ – бісектриса кута АОС. Знайдіть ∠МOC. Розгляньте всі можливі випадки.
668. ОС – бісектриса куга АОВ, ОМ – внутрішній промінь кута АОС. Знайдіть ∠AOМ І ∠AOB, якщо ∠MOC = 60° і ∠АОМ : ∠МOC = 1 : 3.
669. Розгорнутий кут поділено променем на два кути так, що половина одного з них дорівнює третині іншого. Знайдіть ці кути.
670. ОС – бісектриса кута АОВ, М – внутрішня точка кута АОС. Доведіть, що ∠МОС дорівнює піврізниці кутів ВОМ і АОМ.
671. ОС – бісектриса кута АОВ, ОА – бісектриса кута МОС. Доведіть, що ∠МОС дорівнює півсумі кутів АОМ і ВОМ.
672. Є косинець із кутом 50°. Як за його допомогою побудувати кут: 100°; 80°; 160°
До &4
673. ∠AOB і ∠BOC – суміжні кути. Визначте ∠AOB, якщо:
А) ∠BOC = 50°;
Б) ∠BOC більший за ∠OB на 20°;
В) ∠BOC менший від ∠AOB в 4 рази;
Г) ∠AOB : ∠BOC = 3 : 2; г) ∠AOB – ∠BOC = 30°.
674. Один із кутів, утворених при перетині двох прямих, дорівнює 35° 25°. Обчисліть інші кути.
676. Один із кутів, утворених при перетині двох прямих, у 2 рази більший за інший. Визначте міри утворених кутів.
676. Прямі АВ і CD перетинаються в точці О, причому ∠AOC = 130°. Знайдіть кут між бісектрисами кутів:
A) ∠COB і ∠BOD; б) ∠COB і ∠AOD.
677. Прямі АВ і CD перетинаються в точці О. Доведіть, що бісектриси кутів ВОС і АОС перпендикулярні.
678. Прямі АВ і CD перетинаються в точці О. ОЕ – бісектриса кута BOD, ∠DOE = 55°. Знайдіть ∠AOC і ∠COB.
679. ∠AOB і ∠BOC суміжні кути, ОЕ – бісектриса кута ВОС, ∠EOC = = 46°. Доведіть, що ОВ ⏊ АС.
680. Один із кутів, утворених при перетині двох прямих” у 9 разів менший від суми трьох інших кутів. Знайдіть ці кути.
681. Один із кутів, утворених при перетині двох прямих, у 4 рази більший за суму двох суміжних із ним кутів. Обчисліть ці кути.
До &5
682. За допомогою транспортира побудуйте ∠AOB, який дорівнює 70. М – внутрішня точка кута АОВ. Через точку М проведіть прямі, перпендикулярні до сторін кута.
683. За допомогою транспортира побудуйте ∠AOB, який дорівнює 120°. М – внутрішня точка кута АОВ. Через точку М проведіть прямі, паралельні сторонам кута.
684. Площа квадрата ABCD дорівнює 16 см2. Знайдіть відстань від точки А до сторін ВС і CD.
685. Периметр прямокутника ABCD дорівнює 20 см. АВ менша від ВС на 2 см. Побудуйте даний прямокутник і знайдіть відстань від точки А до сторін ВС і CD.
686. ∠AOB і ∠BOC – суміжні кути. Чи перпендикулярні промені ОМ і ON (М – внутрішня точка кута АОВ, N – внутрішня точка кута ВОС), якщо:
А) ∠DOC = 50°, ON – бісектриса кута ВОС, ∠AОМ = 70°;
Б) ∠AОВ : ∠ВОС = 2 : 1, ∠МОВ =  ∠AОВ, ∠CON = 10°;
∠AОВ, ∠CON = 10°;
В) ∠AОВ – ∠ВОС = 20°, ∠MOB = ∠NOC = 40°;
Г) ∠ВОС =  ∠AOB, ∠NOC : ∠NОВ = 1 : 2, ∠AОМ – ∠ВОМ = 24°?
∠AOB, ∠NOC : ∠NОВ = 1 : 2, ∠AОМ – ∠ВОМ = 24°?
До &6
687. Чи паралельні прямі а і b (мал. 262), якщо:
А) ∠1 = 40°, ∠2 = 140°;
Б) ∠1 у 3 рази менший від ∠2, a ∠2 на 90° більший за ∠1;
В) ∠1 : ∠2 = 1 : 4, a ∠1 на 108° менший від ∠2?
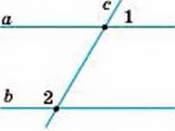
Мал. 262
688. DM – бісектриса кута АВС (мал. 263). Чи паралельні прямі а і b, якщо:
А) ∠1 = 160°, ∠ABM = 80°;
Б) ∠CBM = 60°, ∠1 = 120°;
В) ∠ABM у 2 ради менший від ∠1?
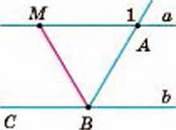
Мал. 263
689. Запишіть пари паралельних прямих (мал. 264), якщо:
А) ∠1 = 120°, ∠2 = 70°, ∠3 = 60°;
Б) ∠1 = 120°, ∠3 = 80°, ∠4 = 100°;
В) ∠2 = 60°, ∠3 = 80°, ∠4 = 120°;
Г) ∠3 = ∠2 = 60°, ∠4 = 120°.
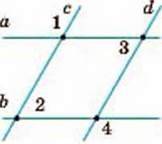
Мал. 264
690. Доведіть, що протилежні сторони квадрата лежать на паралельних прямих.
691. У чотирикутнику ∠BCD ∠BAD у 2 ради менший від ∠ABC, a ∠ABC на 60° більший за ∠BAD. Доведіть, що ВС ‖ AD.
692. У чотирикутнику ABCD пряма BD ділить навпіл ∠ABC і ∠ADC. Чи паралельні протилежні сторони чотири кутника, якщо:
А) ∠ABC = 140°, ∠BDC = 70°;
Б) ∠ABC = ∠ADC?
693. Запишіть пари паралельних прямих (мал. 265), якщо:
А) ∠1 = 70°, ∠2 = 80°, ∠3 = 110°;
Б) ∠1 = 60°, ∠2 = 60°, ∠3 = 100°;
В) ∠1 = 50°, ∠2 = 80°, ∠3 = 100°.
Г) ∠1 = ∠2 = 40°, ∠3 = 140°.
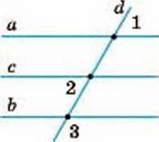
Мал. 265
Мал. 266
Мал. 267
Мал. 268
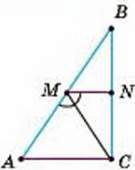
694. Па сторонах АВ і ВС трикутника АВС (мал. 266) узято точки М і N так, що МС – бісектриса кута AMNP, ∠ACM = 50°. Доведіть, що MN ‖ АС, якщо ∠BMN = 80°.
До &7
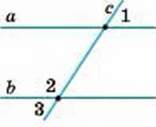
695. Прямі а і b – паралельні (мал. 267). Знайдіть ∠3, якщо:
А) ∠1 = 70°;
Б) ∠1 на 30° менший від ∠2;
В) ∠1 : ∠2 = 4 : 5;
Г) ∠1 становить  ∠2.
∠2.
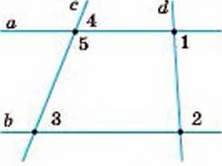
696. Розв’яжіть задачі, користуючись малюнком 268:
А) ∠1 = 80°, ∠2 = 100°, ∠3 = 60°. Знайдіть ∠4;
Б) ∠4 = ∠3, ∠2 = 2 ∠1. Знайдіть ∠1 і ∠2;
В) ∠1 = 55°, ∠2 = 125°, ∠5 : ∠3 = 3 : 1. Знайдіть ∠4;
Г) ∠3 = 70°, ∠5 = 110°, ∠2 – ∠1 = 70°. Знайдіть ∠1 і ∠2.
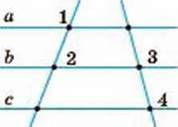
Мал. 269
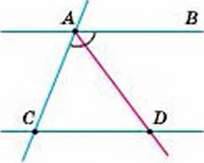
697. АВ ‖ CD, AD – бісектриса кута САВ (мал. 269). ∠ADC = 60°. Знайдіть ∠ACD.
698. Hа сторонах АВ і ВС трикутника ABC взято
Мал. 270
Точки М і N так, що MN ‖ АС (див. мал. 266). ∠ACM = 65°, МС – бісектриса кута AMN. Знайдіть ∠BMN і ∠ВАС.
699. Чи паралельні прямі а і с (мал. 270), якщо:
А) ∠1 + ∠2 = 180°, ∠3 = ∠4;
Б) ∠2 = 60°, ∠3 = 100°, ∠4 = 100°, ∠1 – ∠4 = 30°;
В) ∠2 : ∠3 = 1 : 2, ∠3 – ∠2 = 60°, ∠1 = ∠3, ∠4 = 130°?
До &8
700. Доведіть, що кути, утворені при перетині двох перпендикулярних прямих, – рівні.
701. Доведіть, що зовнішні різносторонні кути, утворені січною з паралельними прямими, – рівні.
702. Доведіть, що зовнішні односторонні кути, утворені січною з паралельними прямими, в сумі дорівнюють 180°.
703. Доведіть, що протилежні сторони прямокутника паралельні.
704. Доведіть, що бісектриси зовнішніх різносторонніх кутів, утворених січною з паралельними прямими, паралельні.
705. Hа прямій послідовно взято точки А, В, С і D. Точка М – середина відрізка ВС, АВ = CD. Доведіть, що точка М – середина відрізка AD.
706. У чотирикутнику ABCD BC ‖ AD. Доведіть, що сума кутів А і В даного чотирикутника дорівнює сумі кутів С і D.
707. У трикутнику ABC Р ∈ АВ, К ∈ ВС, РК ‖ АС. Доведіть, що кути трикутника ABC дорівнюють кутам трикутника РВК.
708. Через точку на площині проведено 4 прямі. Доведіть, що принаймні один із утворених кутів менший від 47°.
До &9
709. Знайдіть периметр трикутника, якщо одна з його сторін дорівнює 5 см, друга – на 3 см більша, а третя – на 3 см менша від суми перших двох сторін.
710. Чи існує трикутник, у якого одна сторона в 2 рази більша за другу, третя – на 1 см менша від другої, а периметр дорівнює 11 см?
711. Дві сторони трикутника дорівнюють 2 см і 3 см. Якому цілому числу сантиметрів може дорівнювати третя сторона трикутника?
712. З вершини В трикутника ABC проведено висоту ВK. Знайдіть довжину відрізка КС, якщо АС = 10 см, АК = 3 см. Розгляньте випадки, коли:
A) ∠A – гострий: б) ∠A – тупий.
713. У ∆АВС проведено висоту ВК. АК : КС = 3 : 6, АС = 16 см. Знайдіть довжину відрізків АК і КС, якщо: a) ∠A – гострий; б) ∠A – тупий.
714. Висота і медіана прямокутного трикутника, проведені з вершини прямого кута, ділять кут на три рівні частини. Знайдіть кут між висотою і бісектрисою, проведеною з цієї вершини.
715. З вершини тупого кута В трикутника ABC проведено висоту, бісектрису і медіану. Кут між бісектрисою і висотою у 2 рази більший за кут між бісектрисою і медіаною. Знайдіть ці кути, якщо кут між висотою і медіаною дорівнює 60°.
До & 10
716. Знайдіть кути трикутника, якщо вони пропорційні числам 2, 3 і 7.
717. Знайдіть внутрішні кути трикутника, якщо один із них у 3 рази більший за інший, а зовнішній кут при третій вершині дорівнює 100°.
718. Знайдіть внутрішні кути трикутника, якщо зовнішні кути пропорційні числам 3, 4 і 5.
719. Знайдіть гострі кути прямокутного трикутника, якщо кут між висотою і бісектрисою, проведеними з вершини прямого кута, дорівнює 20°.
720. У прямокутному трикутнику ABC (∠C = 90°) проведено висоту СН. Доведіть, що ∠HCB = ∠CAB.
721. Знайдіть кути трикутника ABC, якщо ∠B = 100°, а бісектриса ВК є одночасно і висотою.
722. Один із кутів трикутника на 20° більший за другий і на 50° менший від третього. Знайдіть кут між бісектрисами менших кутів цього трикутника.
723. У трикутнику ABC ∠A = 70°, ∠B – 30°. Знайдіть кут між:
А) бісектрисами, проведеними з вершин А і С;
Б) висотами, проведеними з вершин А і С.
724. Доведіть, що кут між висотою і бісектрисою” проведеними з вершини В нерівнобедреного трикутника АВС, дорівнює піврічниці кутів А і С.
До &11
725. Точка М ділить відрізок АВ на два відрізки завдовжки 5 см і 7 см. На які відрізки поділить точка N відрізок CD), якщо CD = АВ i CN : ND = 1 : 5?
726. ∠AOB = ∠COD, ОМ – внутрішній промінь кута COD, ∠COM : ∠MOD = 2 : 3, a ∠MOD – ∠COM = 30°. Знайдіть ∠AOB.
727. ∆АВС = ∆A1B1C1. ∠A = 70°, ∆B = 50°. Знайдіть ∠C1.
728. ∆АВС = ∆A1B1C1, ∠С = 7 см, АВ – ВС = 2 см. Знайдіть сторони трикутника A1B1C1, якщо його периметр дорівнює 21 см.
729. Чи рівні куги трикутників ABC і А1В1С1, якщо ∠A = 70°, ∠C = 80°, а кути трикутника A1B1C1, пропорційні числам 7, 5 і 8?
730. Чи рівні квадрати ABCD і A1B1С1D1, якщо периметр квадрата АВСD дорівнює 20 см, а площа квадрата А1С1D1, дорівнює:
А) 36 см2; б) 25 см2
731. Радіус одного з кіл – 5 см, а довжина другого – 10п см. Чи рівні ці кола?
732. Довжина одного з кіл 14п см, а площа круга, обмеженого другим колом, – 64п см2. Чи рівні ці кола?
До & 12
733. Відрізки АВ і CD перетинаються в точці О. АD ‖ СВ і AD = СВ. Доведіть, що ∆AOD = ∆СОВ.
734. Рівні відрізки АВ і CD перетинаються так, що ∠ABC = ∠BCD. Доведіть, що АС = BD.
735. Дано відрізок АВ і точки С і D такі, що ∠АCB = ∠ADB і ∠CAB = ∠ABD. Доведіть, що АС = BD. Розгляньте випадки, коли точки С і D лежать в одній півплощині відносно прямої АВ і в різних півплощинах.
736. Па паралельних прямих а і b взято точки А, В, С і D, як показано на малюнку 271. АВ = CD. Доведіть, що АС ‖ BD.
Мал. 271
737. Відрізки АВ і CD перетинаються в точці О. АО = СО, ВО = DO. Доведіть, що ∠OBD = ∠ODB.
738. У колі з центром О проведено діаметри АВ і CD. Доведіть, що АС = BD і АС ‖ BD.
739. Hа колі з центром О по один бік від діаметра AD взято точки В і С такі, що ∠AOB = ∠COD. Доведіть, що BD = АС.
740. CD – медіана трикутника ABC, C1D1 – медіана трикутника A1B1C1. Доведіть, що ∆АВС = ∆А1С1, якщо ∆АОС = ∆А1D1C1.
741. ∆АВС = ∆A1D1C1. Доведіть, що бісектриси, проведені з вершин В і B1, – рівні.
742. ∆ABC = ∆A1B1C1. Доведіть, що висоти, проведені з вершин А і A1, – рівні.
743. ∆АОС = ∆A1В1C1. Доведіть, що медіани, проведені з вершин В і B1, – рівні.
До & 13
744. Один із кутів рівнобедреного трикутника дорівнює 110°. Обчисліть інші кути трикутника.
745. Один із кутів рівнобедреного трикутника дорівнює 80°. Обчисліть інші кути трикутника. Скільки розв’язків має задача?
746. Одна зі сторін рівнобедреного трикутника на 3 см більша за іншу. Знайдіть сторони трикутника, якщо його периметр дорівнює 21 см. Розгляньте всі можливі випадки.
747. Hа основі АС рівнобедреного трикутника ABC взято точки М і N такі, що AM = СN. Доведіть, що ∆MBN – рівнобедрений.
748. Один із кутів рівнобедреного трикутника дорівнює 100°. Під яким кутом перетинаються:
А) рівні бісектриси трикутника;
Б) продовження рівних висот трикутника?
749. У ∆АВС медіана АМ перпендикулярна до бісектриси ВК. Знайдіть ВС, якщо АВ = 10 см.
750. Доведіть, що медіани, проведені до бічних сторін рівнобедреного трикутника, – рівні.
751. Відрізки АВ і CD перетинаються в точці О. АО = СО, ВО = DO, АО ≠ ВО. К – точка перетину прямих AD і ВС. Доведіть, що AD KB – рівнобедрений. Розгляньте випадки:
А) АО < ВО; б) АО > ВО.
752. Знайдіть кути рівнобедреного трикутника, якщо кут між бісектрисами, проведеними до бічних сторін, у 2 рази більший за кут при вершині.
753. Знайдіть кути рівнобедреного трикутника, якщо кут при вершині дорівнює куту між бісектрисами, проведеними до основи і до бічної сторони.
754. У рівнобедреному трикутнику ABC кут при вершині В у 2 рази менший за кут при основі. AD – бісектриса, D ∈ BC. Доведіть, що ∆CAD і ∆АОВ – рівнобедрені.
До &14
755. Дано відрізок АВ і точки С та D поза прямою АВ такі, що АС = BD і AD = ВС. Доведіть, що ∆АСВ = ∆BDA. Розгляньте різні випадки розміщення точок С і D.
756. Протилежні сторони чотирикутника ABCD попарно рівні. Доведіть, що ∆АВС = ∆CDA.
757. Протилежні сторони чотирикутника ABCD попарно рівні. Доведіть, що вони паралельні.
758. Відрізки АВ і CD перетинаються в точці О. АО = СО, ВО = DO. Доведіть, що ∆ADB = ∆CBD.
759. Усередині рівнобедреного трикутника АВС з основою АС взято точку D таку, що AD = CD. Доведіть, що ∠ADВ = ∠CDB.
760. Точки С і D лежать по різні боки від прямої АВ, АС = AD і ВС = BD. Доведіть, що АВ – бісектриса кута CAD.
761. Трикутники АСВ і ADB мають спільну основу АВ, АС = AD, ВС = BD. Доведіть, що АВ ⏊ CD.
762. Точки С і D лежать но один бік від прямої АВ, АС = BD і AD = СВ. Доведіть, що ДАОВ – рівнобедрений, де О – точка перетину відрізків AD і ВС.
763. Точки С і D лежать но один бік від прямої АВ, АС = BD і AD = СВ. Доведіть, що ∆АКВ – рівнобедрений, де К – точка перетину прямих АС і BD.
764. У трикутнику АВС ∠А = 70°, ∠D = 80°. Укажіть найбільшу і найменшу сторони трикутника.
766. У трикутнику ABC АВ : 2 = ВС : 3 = АС : 7. Укажіть найбільший і найменший кути трикутника.
766. Доведіть, що найбільша сторона трикутника лежить проти найменшого зовнішнього кута.
767. У трикутнику ABC на стороні АС взято точку К таку, що АВ = К В. Доведіть, що ∠А > ∠С.
768. Висота ВК трикутника ABC ділить сторону АС у відношенні АК : КС = 1 : 3. Порівняйте кути А і С.
769. Дві сторони рівнобедреного трикутника дорівнюють 3 см і 6 см. Визначте третю сторону трикутника.
770. Одна сторона рівнобедреного трикутника дорівнює 39 см, а периметр – 167 см. Знайдіть інші сторони трикутника.
771. Дві сторони трикутника дорівнюють 3 см і 10 см. Яким натуральним числом може виражатися довжина третьої сторони?
772. Одна сторона три кутника дорівнює 0,6 см, друга – у 3 рази більша. Знайдіть периметр трикутника, якщо довжина третьої сторони – натуральне число.
773. Дві сторони рівнобедреного трикутника дорівнюють 5 см і 2 см. Чи може довжина висоти, проведеної до основи, виражатися натуральним числом?
774. Бічна сторона й основа рівнобедреного трикутника відповідно дорівнюють 5 см і 6 см. Знайдіть довжину висоти, проведеної до основи, скориставшись теоремою Піфагора (див. с. 114).
До &16
776. Знайдіть гострі кути прямокутного трикутника, якщо один із них у 4 рази більший за інший.
776. Кут и трикутника пропорційні числам 1, 2 і 3. Доведіть, що трикутник – прямокутний.
777. Один із кутів трикутника дорівнює сумі двох інших. Доведіть, що трикутник – прямокутний.
778. Один із катетів прямокутного трикутника більший за інший на 7 см і менший від гіпотенузи на 1 см. Знайдіть сторони трикутника, якщо його периметр дорівнює 30 см.
779. Медіана трикутника дорівнює половині сторони, до якої вона проведена. Доведіть, що трикутник – прямокутний.
780. Знайдіть менший катет прямокутного трикутника, гіпотенуза якого дорівнює 10 см, а один із кутів – 30°.
781. Гіпотенуза прямокутного трикутника дорівнює 12 см, а один з кутів – 30°. Знайдіть відрізки, на які висота, проведена з вершини прямого кута, ділить гіпотенузу.
782. У трикутнику ABC ∠C = 90°, ∠B = 60°, ВР – бісектриса, ВР = 5 см. Знайдіть АС.
783. У трикутнику ABC ∠C = 90°, ∠А = 30°, СК ⏊ АВ, К ∈ АВ. Знайдіть відстань від точки К до сторони ВС, якщо АС = 8 см.
781. Гіпотенуза рівнобедреного прямокутного трикутника дорівнює 10 см. Знайдіть довжину висоти, проведеної з вершини прямого кута.
785. Катети рівнобедреного прямокутного трикутника дорівнюють по 10 см. СК – висота, проведена з вершини прямого кута. Знайдіть відстань від точки К до катетів.
786. М, N, Р i К – середини сторін квадрата ABCD. Доведіть, що MNPK – квадрат.
До &17
787. Хорда АВ кола з центром О дорівнює радіусу цього кола. Знайдіть ∠AOB.
788. Знайдіть відстань від центра О кола радіуса r до хорди АВ, якщо ∠AOB = 120°.
789. Діаметри АВ і CD кола з центром О – перпендикулярні. Доведіть, що ∠ACB = 90°.
790. У колі з центром О проведено хорди АВ і СD. ∠AOB = 90°, ∠COD = 120. Яка з хорд лежить далі від центра кола і чому?
791. Хорди АВ і CD – паралельні і лежать на однаковій відстані від центра кола. Доведіть, що АВ = CD.
792. Дано два кола з радіусами 3 см і 5 см. Як розміщені ці кола, якщо відстань між їх центрами дорівнює: а) 6 см; б) 8 см; в) 10 см?
793. Два кола дотикаються зовні. Відстань між їх центрами дорівнює 12 см. Знайдіть радіуси цих кіл, якщо один із них більший за інший на 2 см.
794. Два кола мають внутрішній дотик. Відстань між їх центрами дорівнює 8 см. Знайдіть радіуси кіл, якщо один із них у 3 рази менший за інший.
795. Три кола з центрами О1, О2 і О3 попарно дотикаються одне до одного зовнішнім способом. Знайдіть їх радіуси, якщо вони пропорційні числам 2, 3 і 4, а периметр трикутника О1О2О3 дорівнює 36 см.
796. Із точки А до кола проведено дотичні АВ і АС. Пряма КР дотикається до кола в точці М (мал. 272). Знайдіть довжини відрізків АВ і АС, якщо периметр трикутника АКР дорівнює 36 см.
797. Із точки А до кола з центром О проведено дотичні АВ і АС, ∠BOC = 120°, АВ = 7 см. Знайдіть периметр трикутника ABC.
Мал. 272
Мал. 273
798. Знайдіть ширину кільця, утвореного концентричними колами радіусів 10 см і 7 см.
799. Знайдіть радіуси двох концентричних кіл, якщо вони відносяться як 2 : 5, а ширина кільця дорівнює 9 см.
800. Дано два концентричні кола. Із точки А кола радіуса 10 см до кола меншого радіуса проведено дотичні АВ і АС (мал. 273). Знайдіть радіус меншого кола, якщо ∠ВАС = 60°.
До & 18
801. Поділіть даний відрізок у відношенні 1 : 3.
802. Побудуйте прямий кут і проведіть його бісектрису.
803. Побудуйте прямокутний трикутник із катетами 3 см і 4 см.
804. Побудуйте трикутник зі сторонами б см, 7 см і 9 см.
805. Побудуйте рівнобедреник трикутник з основою а і бічною стороною b.
806. Побудуйте рівнобедреник трикутник з основою а і кутом при основі а.
807. Побудуйте гострокутний і тупокутний трикутники та впишіть у них кола.
808. Побудуйте прямокутний трикутник із катетами а і b та опишіть навколо нього коло.
809. Побудуйте трикутник зі сторонами а і b та кутом між ними 120°. Знайдіть центр описаного кола та опишіть це коло.
810. Побудуйте трикутник за двома сторонами і зовнішнім кутом при їх спільній вершині.
811.Накресліть дві паралельні прямі, відстань між якими дорівнює даному відрізку.
До & 19
812. Знайдіть геометричне місце точок, рівновіддалених від кінців хорди АВ кола з центром О.
813. Знайдіть геометричне місце точок, рівно віддалених від кінців основи рівнобедреного трикутника.
814. Знайдіть геометричне місце точок, рівновіддалених від вершин рівностороннього трикутника.
815. Знайдіть геометричне місце точок, рівновіддалених від сторін рівностороннього трикутника.
816. Знайдіть геометричне місце точок, рівновіддалених від двох прямих, що перетинаються.
817. Знайдіть геометричне місце центрів кіл, які дотикаються до двох паралельних прямих.
818. Дано коло з центром О радіуса r. Знайдіть геометричне місце точок, які лежать на відстані 2r від точки О.
819. Дано коло радіуса 10 см. Знайдіть геометричне місце центрів кіл з радіусами 3 см, які з даним колом мають дотик:
А) зовнішній; б) внутрішній.
820. Дано два кола рівних радіусів, які дотикаються зовні. Доведіть, що геометричним місцем точок, рівновіддалених від центрів кіл, є спільна дотична цих кіл, яка проходить через точку дотику.
До &20
821. Кут В прямокутного трикутника ABC дорівнює 60°, катет ВС – 5 см. Знайдіть радіус описаного кола.
822. Сторони прямокутного трикутника ABC дорівнюють 9 см, 12 см і 15 см. Знайдіть радіуси описаного і вписаного кіл.
823. У прямокутний трикутник з гіпотенузою 20 см вписано коло радіуса З см. Знайдіть периметр даного трикутника.
824. Точка дотику кола, вписаного у трикутник, ділять одну з його сторін на відрізки завдовжки 5 см і 7 см. Знайдіть сторони трикутника, якщо його периметр дорівнює 44 см.
825. У трикутнику ABC сторона АС дорівнює 15 см. Точка дотику вписаного в трикутник кола ділить сторону АВ у відношенні 2 :1, починаючи від вершини А. Знайдіть сторони трикутника, якщо йоге периметр дорівнює 42 см.
826. Сторони трикутника дорівнюють 5 см, 7 см і 10 см. Знайдіть відрізки, на які точка дотику вписаного кола ділить найбільшу сторону трикутника.
827. Бічна сторона рівнобедреного трикутника дорівнює: 8 см, кут при основі – 30°. Знайдіть радіус описаного кола.
828. У трикутнику центри вписаного и описаного кіл збігаються. Знайдіть кути трикутника.
829. У трикутник ABC вписано коло, ВС = а. Доведіть, що відстань від точки А до найближчої точки дотику дорівнює р – а, де р – півпериметр трикутника ABC.
830. У прямокутний трикутник зі сторонами АВ = 10 см, АС = 8 см і ВС = 5 см вписано коло. MN – дотична до кола, проведена паралельно до сторони ВС (М ∈ АВ, N ∈ АС). Знайдіть периметр трикутника AMN.
831. Дано ДАВС зі сторонами 7 см, 9 см і 10 см. Hа його менших сторонах АВ і ВС взято точки Р i К такі, що пряма РК дотикається до кола, вписаного в трикутник. Знайдіть периметр трикутника РВК.
До &21
832. Побудуйте трикутник, периметр якого дорівнює 18 см, а сторони пропорційні числам 2, 3 і 4.
833. Побудуйте прямокутник, периметр якого дорівнює: 20 см, а нерівні сторони відносяться як 2 : 3.
831. Дано прямі а і с, що перетинаються, і відрізок КР. Hа його прямій а вкажіть точку, віддалену від прямої с на відстань КР.
835. Побудуйте трикутник за двома сторонами і висотою, проведеною до однієї з цих сторін.
836. За допомогою циркуля і лінійки побудуйте кут, який дорівнює: а) 30°; б) 60°; в) 15°; г)120°; Г)150°; д) 76°.
837. Побудуйте трикутник за двома його зовнішніми кутами і стороною, що з’єднує вершини цих кутів.
838. Опишіть навколо даного кола:
А) квадрат; б) рівносторонній трикутник.
839. Впишіть у дане коло:
А) квадрат; б) рівносторонній трикутник.
840. Дано коло радіуса r. Побудуйте геометричне місце середин його хорд, довжина яких дорівнює r.
841. Дано точки А, В і С. Проведіть через точку А пряму, рівновіддалену від точок В і С.
842. Навколо даного кола опишіть трикутник, два кути якого дані.
843. Побудуйте коло даного радіуса, дотичне до обох сторін даного кута.
844. Побудуйте коло даного радіуса, яке б дотикалося до однієї сторони даного кута і мало б центр на другій його стороні.
845. Побудуйте коло даного радіуса, яке б дотикалося до даної прямої в даній її точці.
846. Побудуйте геометричне місце точок, з яких дане коло видно під: а) прямим кутом; б) кутом 60°.
847. Побудуйте коло, що дотикається до кожного з двох даних концентричних кіл.
ЗАДАЧІ ПІДВИЩЕНОЇ СКЛАДНОСТІ
848. Відстань від Землі до Сонця дорівнює приблизно 149 500 тис. км, а до Місяця – 400 тис. км.
Знайдіть відстань від Місяця до Сонця під час:
А) сонячного затемнення;
Б) місячного затемнення.
849. Точки А, В і С лежать на одній прямій; точки К, Р і Т – середини відрізків АВ, АС і ВС відповідно. Доведіть, що КР = ВТ.
850. Точка С – середина відрізка АВ. Знайдіть на відрізку АВ таку точку X, щоб виконувалась рівність ХА = 1,5 (ХВ + ХС).
851. Один із суміжних кутів v три рази більший за їх різницю. Знайдіть міри цих кутів.
852. Точки А, В, С і D розміщені на площині так, що АВ = ВС = СА і DA = DB = ВС. Знайдіть міру кута ADB.
853. Знайдіть суму кутів А, В, С, В, В, Р і К семикутної зірки (мал. 274).
Мал. 274
854. Всередині трикутника ABC взято довільну точку X. Доведіть, що кут АХС більший за кут ABC.
855. Побудуйте кут на 25 % більший від даного гострого кута.
856. Чи можуть дві висоти трикутника точкою перетину ділитися навпіл?
857. Знайдіть периметр трикутника, якщо від однієї сторони трикутника він більший на а, від другої – на Ь. а від третьої – на с.
858. Доведіть, що сума медіан трикутника менша від його периметра, але більша за півпериметр.
859. Доведіть, що будь-який трикутник можна розрізати на кілька рівнобедрених трикутників.
860. Відрізки АВ і CD перетинаються в точці О так, що АС = АО = ВО = BD. Доведіть, що ОС = OD.
861. Відрізок ВВ1- бісектриса трикутника ABC. Доведіть, що АВ > АВ1 і ВС >В1С.
862. Доведіть, що сума відстаней від довільної точки основи гострокутного рівнобедреного трикутника до його бічних сторін є сталою.
863. У трикутнику АВС АВ = ВС, ∠B = 20°. Hа стороні АВ взято точку М таку, що ВМ = АС. Знайдіть кут ACM.
864. Гострі кути прямокутного трикутника відносяться як 1: 3. Доведіть, що бісектриса ного прямого кута дорівнює одному з катетів.
865. Один із гострих кутів прямокутного трикутника на n° більший за інший. Знайдіть кут між медіаною і висотою трикутника” проведеними з вершини прямого кута.
866. Висота і медіана, проведені з вершини трикутника, ділять його кут на три рівні частини. Знайдіть кути цього трикутника.
867. Доведіть, що кожну сторону трикутника з центра вписаного в нього кола видно під тупим кутом.
868. Навколо рівностороннього трикутника ABC описано коло. Точка К кола лежить усередині кута С. Доведіть, що КА + КВ = КС.
869. Гіпотенуза прямокутного трикутника в 4 рази довша за проведену до неї висоту. Знайдіть міри гострих кутів трикутника.
870. Знайдіть помилку в міркуваннях.
Доведемо, що прямий кут дорівнює тупому. Нехай ∠ABC – тупий, a ∠DAB прямий (мал. 275). Відкладемо AD = ВС, проведемо відрізок DC і серединні пераендикуляри КО і РО до відрізків АВ та CD. Вониперетнуться в деякій точці О, бо прямі АВ і CD – не паралельні. Сполучивши точку О з точками А, В, С і D, одержимо рівні трикутники OAD і ОВС (за трьома сторонами). Отже, ∠OAD = ∠OBC. Кути ОАВ і ОВА також рівні. Тому ∠DAB = ∠ABC, тобто прямий кут дорівнює тупому.
Мал. 275
871. Побудуйте прямокутний трикутник за гіпотенузою і сумою катетів.
872. Побудуйте прямокутний трикутник:
1) за катетом і різницею двох інших його сторін;
2) за гіпотенузою і різницею катетів.
873. Усі вершники на конях, зображені на малюнку 276. – рівні фігури. Знайдіть площу однієї фігури, якщо точки А, В, С і D – вершини чотирикутника площею S.
Мал. 276
874. Побудуйте трикутник за двома кутами і різницею протилежних їм сторін.
875. Дано тупокутний трикутник. Проведіть пряму, що відтинала б від нього такий трикутник, дві сторони і кут якого дорівнювали б двом сторонам і куту даного трикутника.
876. Проведіть частину бісектриси кута, вершина якого недоступна (лежить за межею зошита).
877. Побудуйте трикутник за його периметром і двома кутами.
878. Розв’яжіть кросворд (мал. 277).
По горизонталі:
1. Основне геометричне поняття, що приймається без означення. 6. Наука про геометричні фігури. 7. Захищена споруда в порту. 9. Система умовних знаків для передавання інформації. 11. Пряма, яка має з колом тільки одну спільну точку. 13. Неправильність у міркуваннях, побудовах тощо. 14. Частина геометрії про фігури на площині. 17. Восьма частина прямого кута. 18. Частина площини, обмежена колом. 19. Частина круга. 20. Давньогрецький математик, автор книги “Основи”.
По вертикалі:
2. Чотирикутник з рівними сторонами. 3. Одиниця довжини. 4. Кількісна характеристика предмета або явища. 5. Тисячна частина метра. 7. Відрізок, який сполучає вершину трикутника з серединою протилежної сторони. 8. Одиниця об’єму. 9. Геометрична фігура. 10. Найбільша хорда кола. 12. Твердження, яке приймається без доведення. 13. Прилад для наближеного вимірювання площ. 16. Норма, крайній ступінь обмеження, їв. Латинська літера.

Мал. 277
Про авторів епіграфів
Леонардо да Вінчі (1462-1519) – італійський архітектор, скульптор, художник, винахідник.
Спенсер Герберт (1820-1903) – англійський філософ, соціолог, психолог.
Олександр Степанович Смогоржевський (1896-1969) – український математик.
Прокл Діадох (410-486) – грецький філософ.
