Броунівський рух. Визначення числа Авогадро
ФІЗИКА
Частина 2 МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА
Розділ 5 ЯВИЩА ПЕРЕНЕСЕННЯ
5.2. Броунівський рух. Визначення числа Авогадро
Молекулярно-кінетична теорія особливо бурхливо розвивалася в другій половині XIX ст. переважно завдяки працям Дж. Максвелла і Л. Больцмана. Хоча вона пояснювала багато явищ, проте через відсутність безпосередніх доказів існування молекул і їхнього руху ця теорія не була загальноприйнятою до початку XX ст. Повне визнання молекулярно-кінетичної теорії пов’язане з докладним вивченням так званого броунівського
Англійський ботанік Р. Броун 1827 р. спостерігав під мікроскопом рух у рідині пилку рослин та інших мікроскопічних частинок. Рух мав хаотичний характер, частинки рухалися незалежно одна від одної, описуючи складні зигзагоподібні траєкторії. Інтенсивність броунівського руху зростає з підвищенням температури середовища, зі зменшенням його в’язкості й розмірів самих частинок. Хімічна природа середовища на русі частинок не проявляється. Фізичними поглядами, що панували у першій половині XIX ст., броунівський рух пояснити було неможливо. В кінці XIX ст. під час становлення молекулярно-кінетичної теорії
Перша кількісна теорія броунівського руху з’явилася 1905 р., її автором був А. Ейнштейн. Дослідне підтвердження теорії Ейнштейна, а водночас і молекулярно-кінетичної теорії дав французький фізик Ж. Перрен і його співробітники. Видатні експериментальні дослідження цього вченого, які почалися 1906 р. і продовжувалися кілька років, змусили непримиримих противників кінетичної теорії повірити в реальне існування атомів і молекул.
Якщо в газі або рідині містяться сторонні частинки настільки великі, що за ними можна стежити за допомогою мікроскопа, то ці частинки завдяки ударам об них невидимих молекул середовища братимуть участь у тепловому русі. Природно застосувати до швидкостей броунівських частинок, як і до швидкостей молекул, розподіл Максвелла. Оскільки середня енергія поступального руху молекул визначається співвідношенням (4.15)
То таким самим співвідношенням має визначатися середня кінетична енергія броунівських частинок. За цієї температури середня кінетична енергія броунівських частинок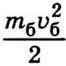 
дорівнює середній кінетичній енергії молекул середовища 
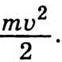Відповідно середні квадратичні швидкості броунівських частинок і молекул зв’язані співвідношенням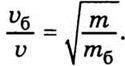 
Подібні уявлення про броунівський рух дали змогу Ж. Перрену дійти такого висновку: якщо розміри броунівських частинок значно менші, ніж середні відстані між ними, то до них можна застосовувати закони ідеального газового стану.
Відповідно до такої ідеї розподіл броунівських частинок у полі сили тяжіння має описуватися формулою Больцмана
Де mg – вага молекули. Цю формулу можна використовувати для описання розподілу молекул в ізотермічній атмосфері, утвореній ідеальним газом, на основі порівняння кількості частинок n2 і n1 в однакових елементарних об’ємах, розміщених на різних висотах h2 i h1. Якщо ж (5.8) застосовувати до броунівських частинок, то потрібно врахувати виштовхувальні сили, які діють на ці частинки з боку середовища, в якому вони розміщуються. Інакше кажучи, у формулі (5.8) замість mg подаємо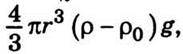 
де ρ – густина броунівських частинок; r – радіус їх; ρ0 – густина середовища. Враховуючи рівність 
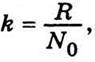вираз (5.8) можна записати так:
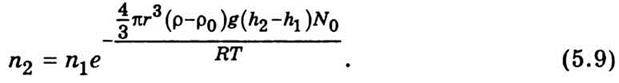
Із співвідношення (5.9) можна визначити число Авогадро:
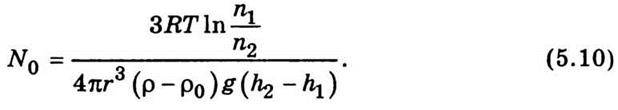
Такий метод визначення числа Авогадро розробив і здійснив Ж. Перрен. Основна складність в його дослідах полягала у виготовленні емульсії з однакових частинок. Проте цю складність усунули: однорідну емульсію одержали зі смолистих речовин центрифугуванням. Емульсію поміщали в плоску кювету з прозорим склом і ретельно термостатували. За допомогою мікроскопа досліджували розподіл завислих частинок на висоті і за даними вимірів визначали число Авогадро. З подібних дослідів Ж. Перрен визначив, що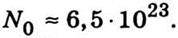 
Це значення досить добре узгоджувалося з результатами визначення числа Авогадро іншими методами.
(1 votes, average: 5.00 out of 5)
Loading...