Дії над натуральними числами
Математика – Алгебра
Натуральні числа і дії над ними
Дії над натуральними числами
Додавання
У записі 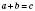 числа a і b – доданки, число с, а також вираз
числа a і b – доданки, число с, а також вираз 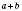 – сума чисел а і b.
– сума чисел а і b.
Властивості додавання
1. Переставна. Від перестановки доданків сума не змінюється: 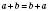 .
.
2. Сполучна. Щоб до суми двох чисел додати третє число, можна до першого числа додати суму другого й третього чисел: 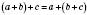 .
.
Переставна й сполучна властивості
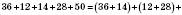
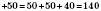 .
.3. Якщо один із двох доданків 0, то їх сума дорівнює другому доданку:
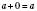 ;
; 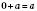 .
.Віднімання
Дія, за допомогою якої за відомою сумою двох доданків і одним із них знаходять другий доданок, називається дією віднімання: 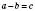 .
.
У цьому записі число а – зменшуване, b – від’ємник, c – різниця.
Різниця двох натуральних чисел показує, на скільки перше число більше від другого або на скільки
Властивості віднімання
1. Щоб відняти суму від числа, можна спочатку відняти від цього числа один доданок, а потім від отриманої різниці – другий:
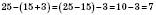 .
.2. Щоб від суми відняти число, можна відняти його від одного з доданків, а до отриманої різниці додати другий доданок:
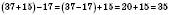 ;
;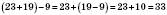 .
.3. Якщо від числа відняти нуль, воно не зміниться:
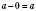 .
.4. Якщо від числа відняти те ж саме число, одержимо 0:
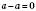 .
.Множення
Помножити число a на число b означає знайти суму b доданків, кожний із яких дорівнює а:
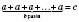 або
або 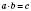 ,
,
де a і b – множники, c – добуток.
Властивості множення
1. Переставна. Від перестановки множників добуток не змінюється:
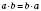 .
.
2. Сполучна. Щоб добуток двох чисел помножити на третє число, можна перше число помножити на добуток другого й третього чисел:
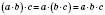 .
.
Сполучна й переставна властивості множення поширюються на довільну кількість множників і дозволяють виконувати множення у довільному порядку: 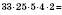
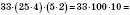
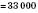 .
.
3. Розподільна.
Щоб помножити суму на число, можна кожний доданок помножити на це число і знайдені добутки додати:
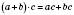 .
.
Щоб помножити різницю на число, можна зменшуване і від’ємник помножити на це число й від першого добутку відняти другий:
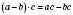 .
.
4. Якщо одиницю помножити на будь-яке число, дістанемо те саме число:
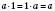 .
.
5. Якщо хоча б один множник дорівнює 0, добуток дорівнює 0:
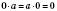 .
.
Приклади
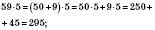
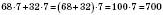 ;
;
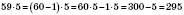 .
.
Ділення
Ділення – дія, за допомогою якої за відомим добутком і одним із множників знаходиться другий множник.
Якщо 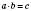 , то
, то 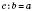 і
і 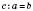 .
.
У записі 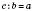 число с – ділене, b – дільник, число а, а також вираз
число с – ділене, b – дільник, число а, а також вираз 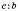 – частка.
– частка.
Частка показує, у скільки разів ділене більше дільника.
Властивості ділення
1. На 0 ділити не можна.
2. Якщо розділити число на 1, дістанемо те саме число: 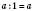 .
.
3. Якщо розділити число на себе, дістанемо 1: 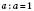
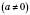 .
.
4. Якщо розділити 0 на будь-яке число, крім 0, дістанемо 0: 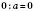
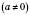 .
.
Ділення з остачею
Число а ділиться на число b націло, якщо 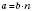 , де n – яке-небудь натуральне число.
, де n – яке-небудь натуральне число.
Наприклад, 15 ділиться націло на 3, оскільки 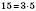 .
.
В іншому випадку можна поділити а на b з остачею. Наприклад:
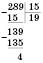
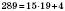 .
.
У цьому записі число 289 – ділене, 15 – дільник, 19 – неповна частка, 4 – остача.
Для будь-яких чисел а та b завжди знайдуться такі числа с і r (натуральні або 0), що 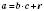 , де
, де 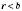 . Коли
. Коли 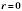 , то
, то 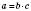 , тобто число а ділиться як на число b, так і на число c.
, тобто число а ділиться як на число b, так і на число c.