Елементи теорії пружності
ФІЗИКА
Частина 1 МЕХАНІКА
Розділ З ОСНОВИ МЕХАНІКИ СУЦІЛЬНОГО СЕРЕДОВИЩА
3.4. Елементи теорії пружності
Розглядаючи механіку твердого тіла, ми користувалися поняттям абсолютно твердого тіла. Однак у природі абсолютно твердих тіл немає, оскільки всі реальні тіла під дією сил змінюють свою форму і розміри, тобто деформуються.
Деформація називається пружною, якщо після припинення дії зовнішніх сил тіло відновлює первинні розміри і форму. Деформацію, що зберігається в тілі після припинення дії зовнішніх сил, називають пластичною
У теорії пружності доводиться, що всі види деформації (розтягу або стиску, зсуву або згину, крутіння тощо) можуть бути зведені до деформації розтягу, стиску і зсуву, які відбуваються одночасно.
Розглянемо однорідний стрижень завдовжки l і площею поперечного перерізу s (рис. 3.10), до кінців якого прикладено сили F1 і F2 (F1 =F2 = F), що спрямовані вздовж
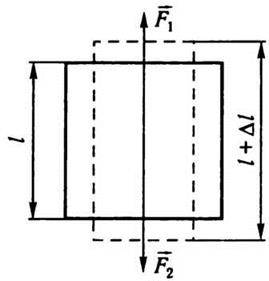
Рис. 3.10
Силу, що діє на одиницю площі поперечного перерізу, називають напруженням:

Якщо сила напрямлена по нормалі до поверхні, то напруження називається нормальним, а якщо по дотичній до поверхні – тангенціальним.
Кількісною мірою, що характеризує ступінь деформації тіла, є відносна деформація. Так, відносна зміна довжини стрижня (поздовжня деформація)

Відносний поперечний розтяг (стиск)

Де d – діаметр стрижня. Величини ε і ε’ завжди мають різні знаки (при розтягу величина Δl позитивна, а Δd – негативна; при стиску, навпаки, Δl – негативна, а Δd – позитивна). Із досвіду випливає взаємозв’язок ε і ε’:
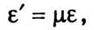
Де μ – позитивний коефіцієнт, що залежить від властивостей матеріалу і називається коефіцієнтом Пуассона.
Англійський фізик Р. Гук (1635-1703) встановив, що для будь-якої малої деформації сила пружності пропорційна деформації, або для малих деформацій напруження а, що виникає всередині тіла, прямо пропорційне відносній деформації є (закон Гука):

Де коефіцієнт пропорційності Е називають модулем Юнга. Із виразу (3.17) видно, що модуль Юнга визначається напруженням, що спричинює відносне видовження, яке дорівнює одиниці. Знак мінус вказує на протилежний напрям напруження і деформації.
Із формул (3.14), (3.15) і (3.17) випливає, що

Або
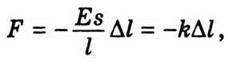
Де k – коефіцієнт пружності. Вираз (3.18) випливає із закону Гука, відповідно до якого видовження стрижня при пружній деформації пропорційне силі, що діє на стрижень.
Деформація твердих тіл описується законом Гука до певної межі. Зв’язок між деформацією і напруженням можна показати у вигляді діаграми напружень, яку розглянемо для металевого зразка (рис. 3.11). Із рисунка видно, що лінійна залежність σ від ε, встановлена Гуком, виконується у дуже вузьких межах до так званої межі пропорційності σп. При подальшому збільшенні напруження деформація ще пружна (хоча залежність σ (ε) уже нелінійна) і до межі пружності σп’ залишкові деформації не виникають. За межами пружності в тілі виникають залишкові деформації і графік, що описує повернення тіла в початкове положення, після припинення дії сили зобразиться кривою СF паралельною ВО. Напруження, при якому виникає помітна залишкова деформація, називають межею текучості σт – точка С на кривій залежності σ (ε). У ділянці СD деформація зростає без збільшення напруження, тобто тіло немов би “тече”. Цю область називають ділянкою текучості (або пластичної деформації).
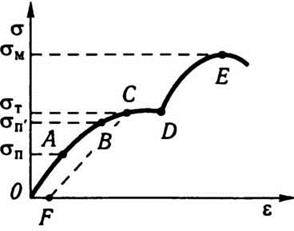
Рис. 3.11
Матеріали, для яких ділянка плинності значна, називають в’язкими, для яких її практично немає – крихкими. При подальшому розтягу (за точку D) тіло руйнується. Максимальне напруження, що виникає в тілі до руйнування, називають границею міцності σм. Діаграма напружень для реальних твердих тіл залежить від різних факторів. Одне й те саме тверде тіло може при короткочасній дії сил виявити крихкі властивості, а при тривалій дії і слабких силах – текучі властивості. Деформацію зсуву найпростіше здійснити, якщо взяти брусок у формі прямокутного паралелепіпеда і прикласти до нього силу F (рис. 3.12), дотичну до поверхні (нижня частина бруска закріплена нерухомо). Відносну деформацію зсуву визначають за формулою

Де Δl – абсолютний зсув паралельних шарів тіла один відносно одного; h – відстань між шарами (для малих кутів 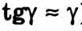 ).
).
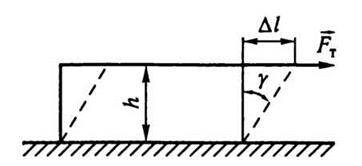
Рис. 3.12