СИЛА ПРУЖНОСТІ. ЗАКОН ГУКА. ДИНАМОМЕТРИ
Розділ ІІІ Взаємодія тіл. Сила
& 22. СИЛА ПРУЖНОСТІ. ЗАКОН ГУКА. ДИНАМОМЕТРИ
Види деформацій
Деформацією називають зміну форми і розмірів тіла. Перелічимо види деформації. Деформація розтягу-стиску виникає, наприклад, якщо ми розтягуємо чи стискаємо пружину (мал. 22.1, випадок 1, 2). Якщо кінці лінійки обертати в різні сторони – отримаємо деформацію кручення (випадок 3). Зігнувши дугою лінійку, ви спричините деформацію згину (випадок 4). Стругаючи ножем дерев’яну паличку, ми здійснюємо деформацію зсуву (випадок 5).
Однак усі
Підвісимо легку пружину так, щоб вона могла вільно зайняти вертикальне положення (мал. 22.3). Довжину пружини у недеформованому стані позначимо l0. Потягнемо вільний кінець пружини з деякою силою F вниз. Довжину пружини після видовження позначимо через l. Різницю l – l0називають видовженням і позначають літерою “х”.
Пружна деформація
Деформація називається пружною, якщо після припинення дії сил, що спричинили деформацію,
Сила, прикладена до пружини видовжуватиме її доти, поки сила пружності, яка напрямлена вгору, не врівноважить цю силу. Якщо припинити дію зовнішньої сили, то сила пружності повертає пружині форму і розмір, що їх вона мала до початку досліду.

Мал. 22.1. Деформація корпусу автомобіля при ударі збоку (креш-тест)
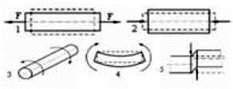
Мал. 22.2. Види деформацій
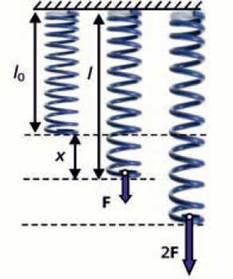
Мал. 22.3. l0 – довжина недеформованої пружини, l – довжина деформованої пружини. Видовження x = l – l0
Прикладемо до пружини вдвічі більшу силу і переконаємося, що видовження стало вдвічі більшим. Утричі більша сила дасть втричі більше видовження.
Закон Гука
До тих пір, поки пружина зберігає пружні властивості, видовження пружини прямо пропорційне величині сили, яка її деформує. Цей простий закон поведінки пружних тіл, відкритий англійським фізиком Робертом Гуком, названо на його честь – закон Гука. В математичній формі закон можна записати так:
F = kx, (22.1)
Де F – це сила, що видовжує пружину. Коефіцієнт пропорційності “к” називають жорсткістю пружини і його можна визначити з формули (22.1) як:
К =  . (22.2)
. (22.2)
Жорсткість вимірюють у Н/м, якщо “X” вимірювати в метрах; або Н/см, якщо x виміряли в сантиметрах. Жорсткість показує, яку силу треба прикласти до пружини, щоб вона видовжилася на одиницю довжини.
Приклад 22.1
Жорсткість пружини k = 0,5 Н/см.
А) Який фізичний зміст вказаного значення жорсткості? б) Складіть таблицю залежності сили F і жорсткості k від видовження х цієї пружини. в) Накресліть графік залежності сили від видовження F(x).
Розв’язання. а) Жорсткість 0,5 Н/см означає, що сила 0,5 Н видовжує пружину на 1 см. Чим більша жорсткість, тим важче пружину розтягувати чи стискати.
Б)
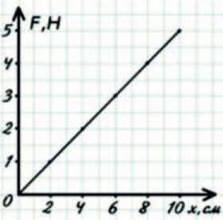
Мал. 22.4. Графік F(x).
Х, см | 2 | 4 | 6 | 8 | 10 |
F, H | 1 | 2 | 3 | 4 | 5 |
К, Н/см | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 |
В) Див. мал. 22.4.
Зауваження. Жорсткість не залежить від прикладеної сили і від величини видовження, тобто є сталою величиною для даної пружини. Це означає також, що графіком F(x) при пружних деформаціях є пряма.
Завдання. Побудуйте на тому самому малюнку (мал. 22.4) графік залежності величини деформуючої сили від видовження пружини, жорсткість якої 1 Н/см.
Динамометр вимірює силу
Прямо пропорційна залежність
Між деформацією “х” та деформуючою силою “F” дозволяє використати пружину для вимірювання сили. Прилад, за допомогою якого вимірюютьвеличину сили, називають динамометром. Цей термін походить від двох грецьких слів: динос – сила і метрон – вимірювати.
Основною деталлю динамометра є стальна пружина. Сталь вибрана тому, що це достатньо пружний матеріал. До вільного кінця пружини прикріплено стрілку, яка рухається вздовж шкали з поділками, проти яких зазначено величину сили (мал. 22.5). Динамометр має обмежувач, який не дозволяє пружині видовжуватися за межі прямої пропорційності.

Мал. 22.5. Вимірювання сили
Приклад 22.2
А) Яка жорсткість пружини динамометра (мал. 22.3), якщо відстань між нульовою і першою позначкою шкали становить 2,5 см? б) З якою силою діє на пружину батарейка?
Розв’язання. а) Згідно формули (16.2) k = 1H/2.5 см = 0,4 Н/см.
Б) Ціна поділки шкали динамометра становить 0,1 Н, отже він показує силу 1,9 Н. Стандартний запис результату вимірювання сили:
F=(1,90±0,05)H
Зауваження. Початкове положення стрілки динамометра не зовсім точно співпадає з нулем шкали, тому тягар діє на пружину з дещо меншою силою, ніж вказує стрілка. Можна спробувати оцінити поправку.
Практична цінність наукового дослідження
При будівництві кораблів, літаків, будинків, мостів, веж використовують балки, які служать опорами або ж перекриттям.
Дослід 22.1
Проведемо простий дослід, ідея якого спричинила революцію в будівельній індустрії. Візьмемо довгий гумовий ластик і ввіткнемо в нього кілька голок так, щоб вони виступали з обох сторін (мал. 22.6). Зігнемо ластик, моделюючи прогин балки. Видно, що з одного боку кінці голок зблизилися, а з іншого – розійшлися. Це свідчить про те, що нижня сторона нашої “балки” стискається, а верхня – розтягується.
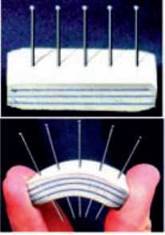
Мал. 22.6. Деформація згину показує, що внутрішня частина гумки не деформується
А як поводить себе середина балки? Очевидно, що вона деформується мало. Це означає, що внутрішня частина балки може бути порожньою без суттєвої шкоди для міцності балки. Круглу суцільну балку можна замінити трубою, прямокутну – П-подібною, Т-подібною, хвилястою (як шифер) або ж схожою на рейки, з яких монтують залізничні колії.
Ви, мабуть, бачили, що залізобетонні плити, якими перекриваються поверхи багатоповерхових будинків, мають усередині трубоподібні порожнини(мал. 22.7). Ці “хитрощі” дають наступні вигоди: а) зменшення затрат матеріалу; б) зменшення ваги конструкції; в) поліпшення тепло – та звукоізоляції.
Другою ідеєю, яка суттєво змінила спосіб будівництва, стало використання армованого залізними прутами бетону. Справа в тому, що залізо добре витримує деформацію розтягу, а бетон міцний “на стиск”. Таким чином залізобетон витримує будь-які деформації.

Мал. 22.7. Конструкції різних профілів
Дослід 22.2
А) Візьміть аркуш паперу й покладіть його краї на дві опори (ними можуть бути дві склянки чи дві сірникові коробки). Отримаєте щось схоже на міст. Під дією власної ваги він прогнеться. б) Потім складіть аркуш, зробивши його гофрованим (мал. 22.8). Який максимальний вантаж із сірникових коробок може витримати така конструкція?

Мал. 22.8. Гофрований папір витримує значний вантаж
Тема для дослідження
22.1. Знайдіть спосіб визначення міцності зовнішньої частини сірникової коробки в різних напрямках.
22.2. Побудуйте модель підвісного моста.
22.3. Як виготовляють і де використовують “попередньо напружений бетон”? Підготуйте на цю тему реферат
Підведемо підсумки
– Закон Гука дозволяє описати усі види деформації.
– Формула закону Гука для пружної деформації розтягу-стиску: F = kx.
– Силу вимірюють динамометром. Основна деталь приладу – стальна пружина.
– Знання фізики деформацій призвело до революції в будівельній індустрії.
Вправа 22
1. При яких деформаціях виконується закон Гука?
2. Яка властивість пружини дозволяє використовувати її як прилад для вимірювання сили?
3. Як деформується середня частина балки при деформації згину?
4. Яка лінія зображає графік F(x) при пружній деформації?
5. Яку ще вигоду крім міцності і малої ваги мають від пустих всередині перекриттів?
6. Назвіть дві ознаки того, що деформація тіла пружна.
7. Чому не прогинається гофрований аркуш паперу?
8. Рама велосипеда зроблена із трубок. Чим це вигідно?
9. Чому пружину динамометра виготовляють зі сталі, а не з міді?
10. Запропонуйте спосіб вимірювання згину балки.
11. Накресліть профіль поперечного перерізу ободу велосипедного колеса.
12. Накресліть профіль перерізу залізничної рейки і поясніть, чому він саме такий.
13. Як деформується: а) трос підвісного мосту; б) самий міст; в) пілони (стовпи, до яких кріпляться троси)?
14. Яку силу покаже динамометр, якщо до нього підвісити дві батарейки (мал. 22.5)?
15. Знайдіть жорсткість пружини, яка видовжується на 3 см під дією сили 36 Н. Виразіть жорсткість в Н/см.
16. Яку силу необхідно прикласти до пружини жорсткістю 20 Н/см, щоб видовжити її на 3 см?
17. Побудуйте два графіки залежності сили, яка деформує пружину, від видовження для пружин, жорсткості яких: а) 2 Н/ см; б) 4 Н/см.
18. За графіком залежності сили, що деформує пружину від видовження визначте жорсткість пружини (мал. 22.9).
19. Якщо дві однакові пружини жорсткістю k з’єднати послідовно одна за одною, то якою буде жорсткість складеної пружини?
20. Запишіть значення сили F, яку показує динамометр (мал. 22.10), визначивши ціну поділки та абсолютну і відносну похибку вимірювання.
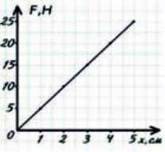
Мал. 22.8. До задачі 18.
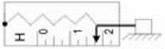
Мал. 22.10.
Роберт Гук (1635-1703). Гук народився 1635 року на острові Уайт у сім’ї церковного служителя. Після закінчення школи навчався в Оксфордському університеті. Спочатку працював асистентом відомого фізика Роберта Бойля, допомагаючи йому конструювати повітряний насос. Гук побудував великий дзеркальний телескоп і відкрив зоряне скупчення в сузір’ї Оріона – так звану Трапецію Оріона, а також уперше помітив, що Юпітер обертається довкола власної осі. Крім того, Гук удосконалив мікроскоп і вивчав будову кристалів, зокрема сніжинок; увів поняття “клітина” в біології; розглядав можливість створення штучних волокон; у 1672 році відкрив дифракцію світла і, щоб пояснити це явище, запропонував хвильову теорію світла. Гук виявився першим, хто довів, що тіла при нагріванні розширюються, і висловив гіпотезу, що повітря складається з маленьких частинок, розташованих на відносно великих відстанях. Він також здогадався, що планети рухаються навколо Сонця по еліпсах і притягаються до нього з силою, обернено пропорційною квадрату відстані від планети до Сонця (але не зумів це довести). Гук запропонував використовувати для дослідження сили тяжіння маятник. У 1660 році вчений відкрив закон пружних деформацій, тобто довів, що пружне видовження твердих тіл пропорційне прикладеній силі. Він навіть зробив спробу теоретично пояснити свій закон взаємодією атомів, з яких складаються тіла, і показав, що жорсткість пружини залежить не тільки від матеріалу пружини, а й від її довжини та площі перерізу. Гук застосував закон пружних деформацій для дослідження годинникових пружин.
