Додавання і віднімання багатоцифрових чисел

НУМЕРАЦІЯ БАГАТОЦИФРОВИХ ЧИСЕЛ

Додавання і віднімання багатоцифрових чисел

374. Прочитай про дію додавання та її закони. Будь-які два натуральних числа можна додати. Числа, які додають, називають доданками, а результат додавання – сумою. Наприклад: 7 + 5 = 12. Тут 7 і 5 – доданки, а 12 – сума. Знак додавання + (плюс). Дію додавання можна визначити за допомогою послідовності натуральних чисел.

Позначимо в цьому ряді число 7. Відлічимо від нього вправо п’ять чисел. Дістанемо число 12, яке називають сумою

Переставний закон додавання. Позначимо в натуральному ряді спочатку число 5, а потім відлічимо від нього вправо сім чисел.

Дістанемо знову число 12. Отже, 7 + 5 = 5 + 7.

Так само для будь-яких натуральних чисел а і b виконується рівність а + b = b + а, яка виражає переставний закон додавання.

Від перестановки доданків сума не змінюється.

Сполучний закон додавання. Додамо три числа 4, 3 і 6. Спочатку до суми чисел 4 і 3, яка дорівнює 7, додамо число 6. Для цього від суми чисел 4 і 3, тобто від числа 7, відлічимо вправо 6 чисел. Дістанемо число 13.

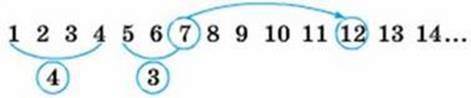
(4 + 3) +

Від числа 4 відлічимо вправо дев’ять чисел. Одержимо 4 + (3 + 6) = 13.

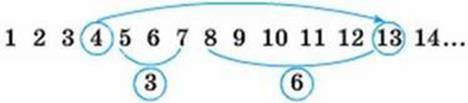
В обох випадках дістали одну й ту саму суму.

(4 + 3) + 6 = 4 + (3 + 6)

Так само для будь-яких натуральних чисел а, b і с виконується рівність (а + b) + с = а + (b + с), що виражає сполучний закон додавання.

Якщо до суми двох чисел потрібно додати третє число, можна до першого додати суму другого і третього.

З переставного та сполучного законів дістаємо ще одну властивість дії додавання.

У сумі кількох доданків можна переставляти доданки і брати їх у дужки будь-яким чином.

Наприклад:

1 + 2 + 3 + 4 = (1 + 4) + (2 + 3)

34 + 249 + 26 = (34 + 26) + 249 = 60 + 249 = 309

375. (Усно.)

237 + 190 + 10 75 + 160 + 40 +125

280 + 467 + 20 289 + 60 + 11 + 13

376. Які з поданих задач розв’язуються дією додавання? Запиши розв’язання цих задач.

1) Від смужки відрізали 8 дм, а потім – ще 5 дм. Скільки всього сантиметрів смужки відрізали?

2) У конверті були листівки. Дівчинка взяла з конверта 8 листівок. У конверті залишилося 4 листівки. Скільки листівок було у конверті спочатку?

3) Перше число а, воно на b менше від другого. Знайди друге число. Склади вираз.

377.

8 + 5 54 + 31 340 + 120 157 + 284 + 343

7 + 6 28 + 17 584 + 175 354 + 168 + 242

378. 356 + 49 + 188 107 + 285 + 74 + 399

379. З двох міст одночасно назустріч один одному вийшли два поїзди. Перший поїзд пройшов до зустрічі 245 км, а другий – на а км більше. Яка відстань між цими містами? Склади вираз для розв’язування задачі та знайди його значення, якщо а = 78.

Розгадай математичний ребус:

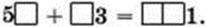
380°. З одного міста одночасно в протилежних напрямках виїхали велосипедист і мотоцикліст. За деякий час велосипедист подолав 42 км, а мотоцикліст за той самий час – на 89 км більше. Знайди відстань між ними в ту мить.

381°.

34 + 25 57 + 28 340 + 200 458 + 249

34 + 20 57 + 1 340 + 20 307 + 127

382. Поясни, як з рівності на додавання склали рівності на віднімання.

8 + 5 = 13 13 – 5 = 8 13 – 8 = 5

383. Прочитай пояснення про дію віднімання.

Відніманням називають дію, за допомогою якої за сумою двох доданків та одним з них знаходять другий доданок. Число, від якого віднімають, називають зменшуваним, число, яке віднімають, – від’ємником, а результат – різницею. Наприклад: 13 – 5 = 8. Тут 13 – зменшуване, 5 – від’ємник, 8 – різниця. Знаходження різниці 13 – 5 можна показати за допомогою натурального ряду.

Позначимо в натуральному ряді число 13. Відлічимо від нього вліво п’ять чисел. Дістанемо число 8.

13 – 5 = 8

Для з’ясування прийомів віднімання важливе значення має правило віднімання суми від числа.

Щоб від числа відняти суму двох інших чисел, достатньо послідовно відняти кожний доданок окремо.

28 – (8 + 9) = (28 – 8) – 9 = 20 – 9 = 11

Так само число можна віднімати частинами.

37 – 9 = 37 – (7 + 2) = (37 – 7) – 2 = 30 – 2 = 28.

384. Які з поданих задач розв’язуються дією віднімання? Запиши розв’язання цих задач.

1) Середньодобовий приріст маси бичка 800 г, а телички – на 70 г менший. Який середньодобовий приріст маси телички?

2) На двох дослідних ділянках посіяли жито й пшеницю. Жита зібрали 22 кг, а пшениці – 36 кг. На скільки кілограмів більше зібрали пшениці, ніж жита?

3) Невідоме число зменшили на 15 і дістали 20. Знайди невідоме число.

4) Сума двох чисел дорівнює 40. Перше з них 8. Знайди друге число.

5) У бензобаку автомобіля було а л бензину. Це на b л більше, ніж залишилося після поїздки. Скільки літрів бензину залишилося в бензобаку? Склади вираз для розв’язування задачі та знайди його значення, якщо а = 80,b = 65.

6) Учень задумав число. Якщо відняти його від 80, то буде 20. Яке число задумав учень?

385.

8 – 7 75 – 23 680 – 350 573 – 268

14 – 8 61 – 25 487 – 259 840 – 352

386. 857 – 509 834 – (400 – 218) 834 – 400 – 218

387. Із 950 кг пшениці намололи 818 кг борошна, а решту становили висівки. На скільки кілограмів більше дістали борошна, ніж висівок?

* Перевір розв’язання, склавши обернену задачу.

388°. Запиши різницю таких чисел: зменшуване k, а від’ємник виражений часткою чисел b і 10. Знайди значення різниці, якщо k = 200, b = 180.

389°.

380 – 200 475 – 258 356 – (104 – 87)

380 – 20 854 – 126 356 – 104 – 87

390. Учневі потрібно було знайти суму й різницю чисел 483 і 255.

Перевір, чи правильно учень виконав завдання. Поясни, як треба записувати числа при письмовому додаванні чи відніманні.

Письмове додавання і віднімання багатоцифрових чисел виконують так само, як додавання і віднімання трицифрових чисел.

391. 1) Виконай дії з поясненням.

45 374 + 8406 5478 – 2349 82 346 – 5478

2) Знайди значення виразів а + b і b – а, якщо:

А) а = 3575 і b = 75 431; б) а = 4306 і b = 54 068.

3) х + 34 013 = 764 354 х – 20 244 = 45 645

392. В овочесховищі зберігалася картопля. Коли звідти вивезли 7250 кг картоплі, залишилося на 3240 кг менше, ніж вивезли. Скільки кілограмів картоплі зберігалося в овочесховищі?

393. З 22 кг бавовняного насіння одержали 5 кг олії. Скільки кілограмів насіння потрібно, щоб одержати 75 кг такої олії?

394*. У хлопчика є 10 білих українських монет. Доведи, що серед них є принаймні 4 однакові монети.

395°.

76 032 + 13 452 89 482 – 76 032

28 340 + 2451 28 340 + 32 451

913 452 – 13 452 5459 – 825

396°. Робітники відремонтували 3650 м шосе, і їм залишилося відремонтувати ще на 1270 м більше. Скільки всього метрів шосе потрібно було відремонтувати?

397. 1) Якщо а – b = с, то b + с = а. Як віднімання перевірити дією додавання?

2) Перевір, чи правильно виконано віднімання: 847 294 – 235 451 = 611 843.

3) Якщо а + b = с, то с – а = b. Як додавання перевірити дією віднімання?

4) Перевір, чи правильно виконано додавання:

29 035 + 43 462 = 72 497.

398.

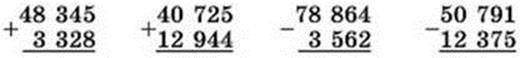
399. На 3 машини навантажили 10 480 кг піску. На першу і другу машини разом навантажили 8350 кг, а на другу і третю – 6180 кг.

Розглянь вирази 10 480 – 8350 і 10 480 – 6180, складені за умовою задачі. Про що дізнаємося, знайшовши їх значення? Виконай обчислення.

400. У трьох цистернах було 10 720 л пального. У першій і третій цистернах разом було 7870 л, у другій і третій – 6020 л. Скільки літрів пального було в третій цистерні?

401. На двох баржах було 18 600 кавунів. Коли з першої баржі вивантажили 2600 кавунів, на обох баржах кавунів стало порівну. Скільки кавунів було на кожній баржі спочатку?

402*. Онук запитав дідуся, скільки тому років. Дідусь відповів: “Якщо проживу ще половину того, що прожив, та ще 1 рік, то мені буде 100 років”. Скільки років дідусеві?

403°. 1) Знайди суму чисел: двісті тисяч чотириста сорок сім і десять тисяч двісті вісім.

2) Зменшуване 90 666, від’ємник 70 238. Знайди різницю.

3) Зменш 87 840 на 9535.

4) Обчисли і перевір: 28 540 – 6807, 13 575 + 95 880.

404°. За даними таблиці знайди, скільки тканини використали для пошиття однієї наволочки.

405. Заповни таблицю.

406. 1) Поясни обчислення.

2) Виконай дії письмово.

1998 + 8 2000 – 2 10 008 – 125 100 000 – 37

407. Виконай дії і зроби перевірку.

307 857 + 84 408 67 082 – 9556

408. За 3 місяці завод випустив 4603 автомобілі. Скільки автомобілів випустив завод окремо за кожний місяць, якщо за перший і другий місяці він випустив 2978 автомобілів, а за перший і третій місяці – 3093?

409*. Дріт завдовжки 250 м розрізали на 3 частини. Дві з них рівні між собою, а третя частина на 10 м довша від кожної з перших двох. Яка довжина більшої частини дроту?

410°. Маса автомобілів “Таврія”, “Ланос” і “Нива” разом 4120 кг. Яка маса кожного окремо, якщо маса “Таврії” і “Ланоса” 2020 кг, а маса “Ланоса” і “Ниви” 3460 кг?

411°.

56 + 185 + 357 121 393 – 65 850

375 + 109 – 251 69 760 – 23 580

68 000 : 100 720 – 20 ∙ 7

412. (Усно.) 1) Зменш на 4 тис. кожне число: 55 778; 9000; 60 000; 4375.

2) 1 ∙ 12 – 7 250 ∙ 100 + 1 60 000 : 100 – 10

413. Обчисли з коментуванням.

25 + 43 + 35 + 37 + 20 180 + 230 + 20 + 70

414. 30 001 – 7 40 004 – 38 700 020 – 30 003

415. Перевір, чи правильно виконано додавання.

416. Обчисли суми, записуючи доданки стовпчиком.

57 453 + 8480 + 876 3405 + 34005 + 25 788

417. Довжина Південного Бугу 806 км. Дністер на 556 км довший за Південний Буг. Дніпро на 839 км довший за Дністер. Знайди довжину Дніпра.

Південний Буг Дністер Дніпро

418. Периметр трикутника 12 см 6 мм. Довжина однієї сторони 4 см 8 мм, другої – 3 см 9 мм. Знайди довжину третьої сторони.

419. Віднови нерівності.

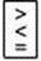
240 – 80 < 300 – 80 350 – 70 … 350 – 40

240 + 80 … 300 + 80 350 + 70 … 350 + 40

420°. У першому овочесховищі було 3850 ц капусти, а в другому – 4090 ц. У перше овочесховище привезли ще 358 ц капусти, а в друге – 245 ц. У якому овочесховищі стало більше капусти й на скільки центнерів?

421. (Усно.)

35 – 7 – 8 40 – 8 ∙ 2 58 – 8 + 16

42 + 8 – 14 40 : 8 ∙ 2 56 : 8 +17

422. Запиши в метрах: 5 км 600 м; 2 км 80 м; 1000 см; у сантиметрах: 4 м; 8 м 20 см; 10 м 5 см; 300 мм.

423. Обчисли.

50 778 – 21 930 – 19 855 5888 – 3409 + 1758

54 127 +(25 705 – 9777) 17 788 – (9473 – 6207)

424. Розглянь розв’язання задачі з буквеними даними.

Задача. Крісло коштує b грн, а стілець – у 3 рази дешевший. Скільки коштують крісло й стілець разом?

Розв’язання:

B – вартість крісла;

B : 3 – вартість стільця;

B + b : 3 – вартість крісла й стільця разом.

425. Перше число с, а друге – у 4 рази більше. Знайди суму цих чисел. Склади вираз та обчисли його, якщо с = 224.

426. Склади й розв’яжи задачу.

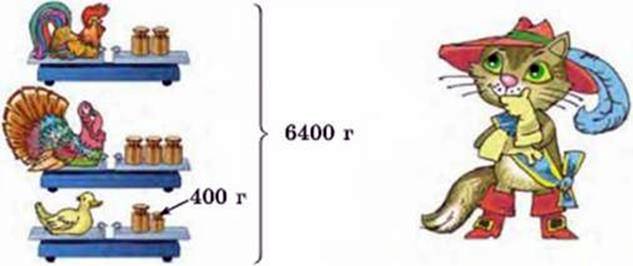
427. Знайди масу кожного птаха.

428. Із чисел 1, 5, 20, 30 випиши ті значення змінної, для яких істинні нерівності.

60 : k > 4 50 – k < 25 17 + k > 40

429°. З двох клубків вовни сплели 3 шапочки. Скільки таких шапочок можна сплести з 10 клубків?

430°. 72 420 – (11 725 – 9428) 7807 – (3655 + 977)

ДОДАВАННЯ І ВІДНІМАННЯ ІМЕНОВАНИХ ЧИСЕЛ

431. (Усно.)

1т – 250 кг 10 т – 2 ц

1 м – 37 см 10 дм – 4 см

2 кг – 300 г 2 м – 30 см

432. 1) Перевір, чи правильно виконано віднімання, і поясни, чим різняться подані записи.

53 м 08 см – 9 м 73 см = 43 м 35 см

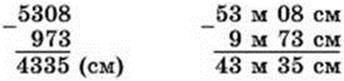
2) Знайди різницю і суму: 7 км 080 м і 5 км 185 м.

433. За 10 с дівчинка налічила в себе 12 ударів пульсу. Скільки ударів налічить дівчинка за хвилину?

434. 1) Перевір, чи правильно виконано додавання.

27 т 459 кг + 9 т 780 кг = 37 т 239 кг

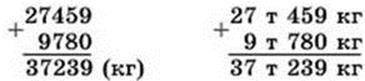
2) Знайди суму і різницю: 19 кг 450 г і 7 кг 080 г.

435. Маса гуски 5 кг 720 г, курки – на 3 кг 345 г менша, ніж гуски, а індика – на 4 кг 390 г більша, ніж маса гуски й курки разом. Яка маса курки, гуски та індика разом?

436. Маса 50 однакових пакетів борошна 1 ц 50 кг. Яка маса 100 таких пакетів?

437°. Придбали 180 л бензину. Для заправлення автомобіля використали третю частину бензину, а трьох мотоциклів – по 9 л бензину. Скільки літрів бензину залишилося?

438°.

10 ц 9 кг – 5 ц 68 кг 25 073 – (785 + 7453)

5 кг 708 г + 4 кг 840 г 49 507 – (4305 – 947)

439. Прочитай тільки числа, що закінчуються нулем: 15; 40; 99; 100; 151; 250; 1000; 1009; 1200.

Як називають числа, що закінчуються нулем або кількома нулями? 40, 100, 250, 1000, 1200 – круглі числа.

440. Кожне число можна записати у вигляді суми або різниці круглого й одноцифрового чисел. Наприклад:

37 = 30 + 7 37 = 40 – 3

152 = 150 + 2 152 = 160 – 8

Запиши кожне із чисел 76 і 379 у вигляді суми й різниці круглого та одноцифрового чисел.

441. Розв’яжи задачу складанням виразу.

З міста в село вийшов турист, а із села назустріч йому виїхав велосипедист. До зустрічі турист пройшов с км, а велосипедист проїхав у 3 рази більшу відстань. Яка відстань між містом і селом?

442. 340 055 – 43 380 424 888 – 285 099

443. Знайди периметр кожної ділянки за планом.

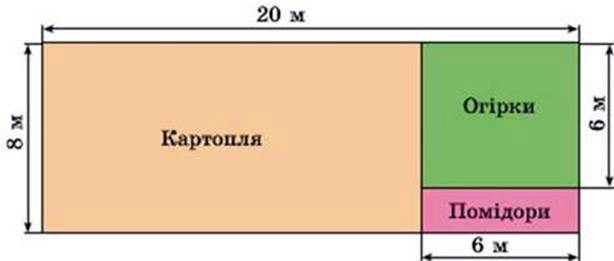
444. Першого дня фабрика виробила 13 730 м тканини, другого дня – стільки ж, скільки першого, а третього – на 11 800 м менше, ніж першого і другого разом. Скільки всього метрів тканини фабрика виробила за 3 дні?

445. Склада і розв’яжи задачі за короткими записами.

1)

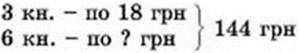
2)

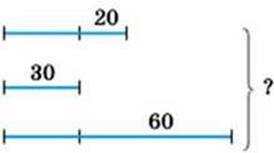
446°. Зі складу вивезли вугілля на 15 вантажівках, по 3 т на кожній. На складі залишилося 60 т вугілля. Про що дізнаємося, обчисливши вирази?

3 ∙ 15 60 : 3 3 ∙ 15 + 60 60 – 3 ∙ 15 15 + 60 : 3

447°.

185 407 + 20 470 + 338 7 922 т 75 кг – 990 кг

25 754 – (9457 – 7090) (2 ц – 50 кг) : 2

448. Відстань від міста А до міста В поїзд подолав за 5 год 48 хв, а від міста В до міста С – за 3 год 34 хв. Скільки часу поїзд був у дорозі? Поясни обчислення.

Розв’язання:

5 год 48 хв + 3 год 34 хв = 9 год 22 хв

449. Перевір обчислення.

450. Обчисли.

15 год 16 хв + 9 год 49 хв 10 хв 30 с + 25 хв 45 с

5 діб 6 год – 2 доби 18 год 7 год 34 хв – 2 год 40 хв

451. У стійловий період одній корові згодовували за день 37 кг силосу. Стійловий період тривав з 25 жовтня по 10 травня. Скільки кілограмів силосу згодували 96 коровам за третину стійлового періоду?

452. Перша зерноочисна машина за 6 хв очищає 90 кг зерна, а друга за 4 хв – 80 кг зерна. За який час обидві машини разом очистять 7 т зерна?

453°. Дві бригади зібрали 24 корзини моркви, усього 288 кг. Перша бригада зібрала 156 кг моркви, а друга – решту. Скільки корзин моркви зібрала кожна бригада?

454°. Обчисли.

21 год 17 хв – 12 год 45 хв 7 хв 12 с – 5 хв 16 с

9 год 16 хв + 8 год 57 хв 11 р. 4 міс. – 6 р. 6 міс.

455. (Усно).

2 год – 35 хв 3 доби – 6 год 3 год 20 хв – 50 хв

4 хв – 26 с 5 діб 4 год – 8 год 10 год – 7 хв

456. Знайди різниці та перевір дією додавання.

14 год 35 хв – 8 год 57 хв

16 діб 10 год – 6 діб 15 год

457. Магазин розпочинає роботу о 8 год ранку, а зачиняється о 9 год вечора. Скільки годин працює магазин, якщо обідня перерва триває 1 год? (Розв’яжи задачу за допомогою годинникового циферблата.)

458. Розглянь розв’язання задач на визначення тривалості події, її закінчення та початку.

Задача 1. Перерва розпочалась о 10 год 10 хв і закінчилась о 10 год 30 хв. Скільки часу вона тривала?

10 год 30 хв – 10 год 10 хв = 20 хв

Задача 2. Перерва розпочалась о 9 год 15 хв і тривала 10 хв. Коли вона закінчилася?

9 год 15 хв + 10 хв = 9 год 25 хв

Задача 3. Перерва тривала 30 хв і закінчилась о 10 год 35 хв. Коли вона розпочалася?

10 год 35 хв – 30 хв = 10 год 5 хв

459. Сонце зійшло о 7 год 55 хв ранку, а зайшло о 4 год 16 хв вечора. Визнач тривалість дня.

460*. З трьох учнів на ім’я Тимко, Андрійко і Сергій – ко двоє – відмінники. Визнач, хто відмінник, якщо в парі Тимко й Андрійко – один відмінник, один – ні, а в парі Андрійко і Сергійко – теж один відмінник, один – ні.

461°. 1) Сонце зійшло о 6 год 35 хв. Тривалість дня становила 11 год 10 хв. Визнач час заходу Сонця.

2) Тривалість дня – 16 год 17 хв. Сонце зайшло о 9 год 5 хв вечора. Визнач час сходу Сонця.

462°.

160 034 : 46 600 280 – 158 430 349 ∙ 86

30 014 ∙20 88 370 + 71 684 441 850 : 5

463. Обчисли вирази, у яких другою є дія ділення.

480 : 6 – 16 240 – 80 : 4 + 100

60 ∙ 4 : 30 + 100 60 + 100 : 4 ∙ З

(500 + 300) : 2 – 250 560 : 8 – 10 ∙ 4

464. Розглянь розв’язання задачі на визначення часу. Задача. Учні виїхали на екскурсію 7 вересня о 10 год ранку, а повернулися 15 вересня о 8 год вечора. Скільки часу тривала екскурсія?

Розв’язання:

1) Екскурсія розпочалася, коли минуло 6 діб 10 год від початку вересня.

Екскурсія закінчилася, коли минуло 14 діб 20 год від початку вересня.

14 діб 20 год – 6 діб 10 год = 8 діб 10 год

465. Гетьман українського реєстрового козацтва Петро Сагайдачний помер 20 квітня 1622 р. Скільки минуло часу з дня його смерті до сьогоднішнього дня?

466. З пункту А поїзд вийшов 22 травня о 6 год вечора і у пункт Б прибув 25 травня о 9 год ранку. Скільки часу поїзд був у дорозі?

Гетьман Петро Сагайдачний

467. Теплохід ішов від Миколаєва до Одеси. Коли він пробув у дорозі 2 год 45 хв, йому залишилося йти на 13 год 10 хв більше, ніж він ішов. За який час теплохід має пройти шлях від Миколаєва до Одеси?

468. Тарас Шевченко народився 9 березня 1814 року. Скільки років, місяців і днів минуло з того часу?

469. Розв’яжи рівняння з перевіркою.

1083 – х = 137 х – 2604 = 1074 2370 + х = 1230

470*. Накресли на прямій відрізки АВ = 2 см 3 мм, ВС = 3 см та С К = 5 см 4 мм. Знайди довжину АК. (Розглянь різні випадки.)

471°.

560 : 70 + 2730 (7 ц 50 кг – 70 кг) : 5 кг

3920 – 390 ∙ 5 3 т 4 ц – 540 кг

472°. Екскурсія містом триває 3 год 20 хв. Початок екскурсії о 8 год 10 хв, о 12 год, о 16 год. На які екскурсії може піти турист, якщо йому треба встигнути на поїзд, який від’їжджає о 18 год?

473. Щоб додати або відняти числа, іноді доцільно користуватися способом округлення. Розглянь записи й поясни, як застосовується спосіб округлення.

474. Обчисли, застосовуючи спосіб округлення.

38 + 18 47 + 99 360 – 37 92 – 46 485 + 198

475. Із чисел 1, 3, 5, 8, 10 вибери ті значення букви для яких істинна кожна нерівність.

30 ∙ х > 100 240 : х < 120 20 – х > 12

476. У спортивному таборі було 217 дітей. На змагання з футболу виїхало кілька команд, по 11 гравців у кожній. У таборі залишилося 173 дитини. Скільки футбольних команд виїхало на змагання?

477. Господарство планувало здати 3250 кг масла. Але воно здало 3800 кг, а потім – ще 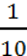цієї кількості.

На скільки більше кілограмів масла господарство здало, ніж планувало?

478. Довжина відрізка АВ дорівнює 6 см. Радіус кола із центром у точці А дорівнює 1 см 2 мм, а із центром у точці В – 9 мм. Знайди відстані КМ і CD. (Результати обчислень перевір вимірюванням.)

479. Тарас купив 10 зошитів, а Юрко – 8. До них приєднався Олесь, і вони поділили всі зошити порівну. Олесь повернув їм за зошити 36 грн. Скільки грошей із цієї суми одержить Тарас і скільки – Юрко?

480°. Обчисли, записуючи лише вираз і його значення.

64 + 19 235 + 98 117 + 37 218 – 29

620 + 178 140 – 87 2400 – 388 167 + 395

481°. У академії, коледжі й ліцеї навчається всього 8658 студентів. Скільки студентів навчається окремо в академії, коледжі й ліцеї, якщо в академії і коледжі навчається 5087 студентів, а в коледжі й ліцеї – 4756?

482. Співвідношення між величинами можна наочно зобразити стовпчиками або відрізками.

Нехай маємо дані про максимальну довжину деяких морських тварин: китова акула – 15 м; біла акула – 11 м; тигрова акула – 5 м 5 дм; акула-молот – 4 м 5 дм.

Накреслимо прямий кут і позначимо на його горизонтальній стороні назви акул, а на вертикальній – шкалу довжини. Тоді довжину акул можна зобразити стовпчиками відповідної висоти. Вийде стовпчаста діаграма. Якщо замість стовпчиків накреслити відрізки, то вийде лінійна діаграма.

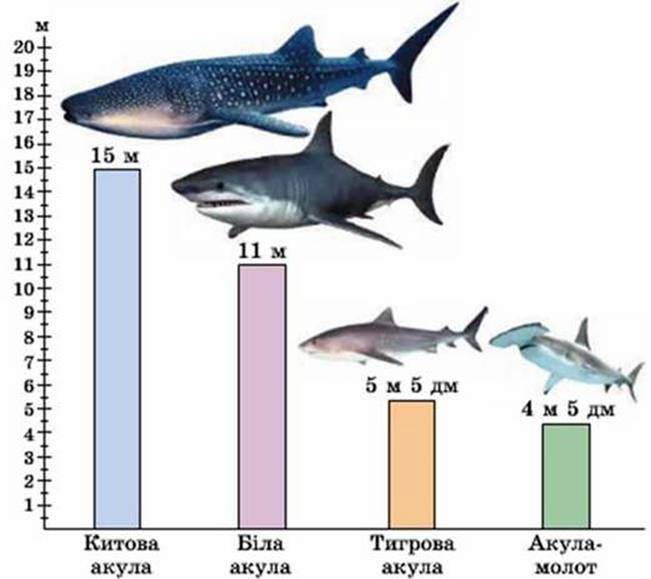
За діаграмами визначають особливості відношень між величинами. На нашій діаграмі видно, що найдовшою є китова акула, акула-молот коротша від білої тощо.

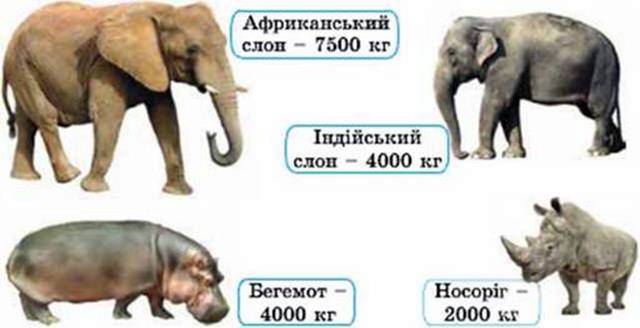
483. Побудуй лінійну або стовпчасту діаграму найбільших мас тварин. Склади задачі за цими даними.

484. Поїзд був у дорозі 3 год і пройшов 230 км. За першу годину він пройшов 78 км 500 м. Це на 6 км більше, ніж за другу годину. Який шлях пройшов поїзд за третю годину?

485.

198 + 250 3640 + 87 3648 + 350

397 + 150 2630 – 287 1648 – 350

269 + 2199 1269 – 199 1648 – 550

486. Коли зі складу вивезли 8 вантажівок овочів, по 24 ц на кожній, залишилося ще на 215 ц овочів більше, ніж вивезли. Скільки центнерів овочів було на складі спочатку?

487*. Відомо, що а ∙ b = 240. Чому дорівнює а ∙ (b – 8), якщо а = 20?

488°.

5 т 970 кг + 56 ц 15 км – 8 км 500 м

12 т – 3 ц 40 кг 12 км 390 м + 1 км 510 м

489°. Для кролів заготовили 1400 кг коренеплодів і 1250 кг картоплі. За півроку згодували 870 кг коренеплодів, це на 180 кг більше, ніж картоплі. Якого корму залишилося більше і на скільки кілограмів?