ДОДАВАННЯ СИЛ. РІВНОДІЙНА. МАСА І СИЛА
Розділ ІІІ Взаємодія тіл. Сила
& 23. ДОДАВАННЯ СИЛ. РІВНОДІЙНА. МАСА І СИЛА
Якщо на тіло діє декілька сил, то їх можна замінити однією, яку називають рівнодійною силою.
Графічне зображення сил. Додавання сил, напрямлених вздовж однієї прямої
Розглянемо сили, що діють вздовж однієї прямої.
А) Коли сили напрямлені в один бік, то величина їх рівнодійної дорівнює сумі величин цих сил і направлена в той самий бік.
Б) Якщо сили протилежно напрямлені, то величина їх рівнодійної дорівнює різниці величин цих сил і напрямлена в бік
На мал. 23.1 вибрано масштаб, при якому 1 см відповідає силі 1 Н. Тоді сила F1 = 4H зобразиться вектором, довжина якого становить 4 см, а силаF2 = 3H – вектором, довжина якого становить 3 см.
Рівнодійну сил F1 і F2 позначимо як F, це записують так: F = F1 + F2.
У випадку а) результат спільної дії сил F1 і F2 на дане тіло буде такий
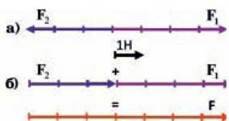
Мал. 23.1.
А) Сили віднімаються, коли вони напрямлені в протилежні сторони. б) Сили додаються, коли вони діють в одному напрямі
Самий, як у сили F величиною 1 H, направленої вправо. У випадку б), коли сили F1 і F2 діють в одному напрямі, їх рівнодійна дорівнює
Додавання сил, напрямлених довільним чином
Сили додаються як вектори, тобто так само, як переміщення і швидкості (мал. 23.2). При додаванні сил прийнято проводити їх з однієї точки (точки прикладання), як на мал. 23.3. Очевидно, що результат додавання сил за правилом трикутника і правилом паралелограма однаковий. Намал. 23.4. зображено частинний випадок, коли сили напрямлені під прямим кутом. У кожному випадку рівнодійна сила F = F1 + F2. Як вже говорилося в попередніх параграфах, отримати числове значення суми сил, направлених довільним чином, можна, вибравши довжину стрілок в певному масштабі.
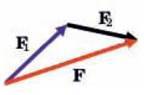
Мал. 23.2. Додавання сил за правилом трикутника
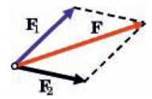
Мал. 23.3. Додавання сил за правилом паралелограма
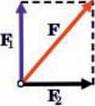
Мал. 23.4. Додавання сил, напрямлених під прямим кутом
Приклад 23.1
На тіло в точці А (мал. 23.5) діють три сили, пронумеровані як 1, 2 і 3. Яким буде результат дії цих сил на тіло?
Розв’язання. Знайдемо рівнодійну сил 1 і 3. З мал. 23.6 видно, що рівнодійна цих сил є вектор сили 4, який компенсує силу 2. Отже, рівнодійна сил в точці А дорівнює нулю і тіло не змінюватиме свій стан руху.
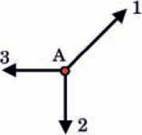
Мал. 23.5. На тіло в точці А діють три сили
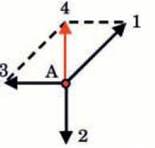
Мал. 23.6. Замінимо сили 1 і 3 рівнодійною 5
Сила, маса і прискорення
Прискорення тіла залежить від величини рівнодійної тих сил, що на нього діють і від маси тіла. Чим більша, наприклад, маса автомобіля, тим повільніше він буде набирати швидкість при даній силі тяги, тобто тим меншим буде його прискорення. Маса тіла є мірою інертності цього тіла, і чим більша маса, тим більше зусилля потрібно прикласти, щоб змінити швидкість тіла, тобто надати йому прискорення. Цей факт відображено у другому законі Ньютона:
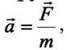(23.1)
Де “т” – маса тіла, “а” – його прискорення, а F – рівнодійна сил тяги і сил тертя, тобто їх різниця (бо вони протилежні).
Формула (23.1) показує, що прискорення “а” тіла буде тим більшим, чим більшою є рівнодійна сил, які на нього діють (при незмінній масі), і прискорення “а” тим менше, чим більша маса тіла (при незмінній рівнодійній силі).
Залежно від того, направлена рівнодійна сила вперед чи назад, тіло збільшуватиме чи зменшуватиме свою швидкість.
Силу вимірюють у ньютонах (Н), масу в кілограмах (кг), а прискорення у м/с2 . Згідно формули F = m ∙ а, яку можна отримати з (23.1): Н = кг ∙ м/с2 – це означає, що рівнодійна сила 1 Н надає тілу масою 1 кг прискорення 1 м/с2 у напрямі, що співпадає з напрямом рівнодійної сили.
Приклад 23.2
Два однакових за масою автомобілі стартують одночасно. Рівнодійна сили тяги і сил опору першого автомобіля вдвічі більша за рівнодійну сил другого (мал. 23.7). У результаті через 10 секунд (характерний відрізок часу для старт – тестів) перший автомобіль розвине у два рази більшу швидкість (тобто рухатиметься з прискоренням, яке вдвічі більше від прискорення другого автомобіля).
Мал. 23.7. При однакових масах вперед вирветься той автомобіль, у якого сильніший двигун
Приклад 23.3
Двигуни двох автомобілів, розвивають однакові зусилля. Маси автомобілів відрізняються втричі. За однаковий час від моменту старту автомобіль меншої маси розвине втричі більшу швидкість (мал. 23.8).
Щоб два тіла з різними масами рухалися з однаковими прискореннями, потрібно до тіла більшої маси прикласти більшу силу.
Якщо потрібно збільшити швидкість тіла, треба подіяти на нього силою, яка збігається з напрямком його швидкості. І навпаки, для зменшення швидкості, сила має бути направлена проти напрямку руху.
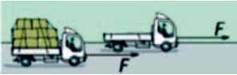
Мал. 23.8. При однаковій силі двигунів вперед вирветься менший за масою автомобіль
Підведемо підсумки
– Якщо на тіло діє декілька сил, їх потрібно векторно додати. Результат додавання називають рівнодійною всіх доданих сил:
F = F1 + F2 .
– Прискорення тіла прямо пропорційне рівнодійній силі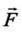 
і обернено пропорційне масі тіла: 
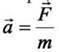– ІІ закон Ньютона.
– Маса тіла є мірою його інертності (цю масу називають інертною).
Вправа 23
1. Якщо на тіло діє декілька сил, то як називають їх векторну суму?
2. Якщо сили напрямлені вздовж прямої в одну сторону, то чому дорівнює величина і напрям рівнодійної цих сил?
3. Якщо сили напрямлені вздовж прямої в протилежні сторони, то чому дорівнює величина і напрям рівнодійної цих сил?
4. Як зміниться прискорення тіла, якщо: а) при незмінній масі збільшити рівнодійну силу? б) при незмінній рівнодійній силі збільшити масу тіла?
5. Як виразити одиницю вимірювання сили через основні одиниці СІ?
6. Яку властивість тіла описує маса при дії на тіло сил, що не компенсуються?
7. Масу автомобіля збільшили в п’ять разів, не змінюючи силу тяги двигуна. Як зміниться його прискорення?
8. Як зміниться прискорення тіла, якщо його масу і значення рівнодійної сили збільшити в однакову кількість раз?
9. Упродовж трьох секунд тіло масою 5 кг збільшило швидкість від 6 до 18 м/с. Обчисліть величину сили, яка діяла на тіло.
10. На тіло масою 2 кг діє направлена вправо рівнодійна сила 10 Н. а) Яким буде напрям прискорення і його величина?
Б) На скільки зросте швидкість тіла за дві секунди?
11. а) Якою була рівнодійна сила, що діяла на менш потужний автомобіль в прикладі 23.2, якщо за 10 с він зі старту набрав швидкість 72 км/год.? Маса автомобіля 1500 кг. б) Яку швидкість набрав більш потужний автомобіль?
12. У скільки разів відрізняються прискорення автомобілів у прикладі 23.3?
13. Яка маса тіла, якщо сила 24 Н надала йому прискорення 6 м/с2?
14. На тіло в точці А (мал. 23.9) діють чотири сили, пронумеровані як 1, 2 3 і 4. Величина четвертої сили становить 5 Н.
А) Яка величина рівнодійної цих сил і куди вона напрямлена?
Б) Яку силу потрібно забрати, щоб тіло знаходилось в стані спокою?
15. Величина вектора сили F1 дорівнює 2 Н (мал. 23.10). а)
Яка величина і напрям рівнодійної усіх трьох сил? б) Чому дорівнює величина сили F2 і F3?
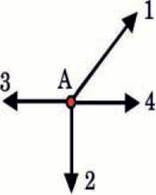
Мал. 23.9. До задачі 13
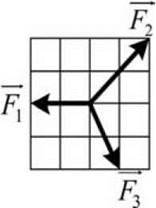
Мал. 23.10. До задачі 14
(1 votes, average: 5.00 out of 5)
Loading...