Енергія магнітного і електромагнітного полів
ФІЗИКА
Частина 3 ЕЛЕКТРИКА І МАГНЕТИЗМ
Розділ 9 МАГНЕТИЗМ. МАГНІТНЕ ПОЛЕ ЕЛЕКТРИЧНОГО СТРУМУ
9.10. Енергія магнітного і електромагнітного полів
Магнітне поле є виявом електричного струму. Струм завжди утворює навколо себе магнітне поле. Будь-яка зміна струму приводить до зміни індукції його магнітного поля, і, навпаки, всяка зміна індукції магнітного поля спричинює появу електричного поля, а отже, струму в колі. Це дає змогу зробити висновок, що енергія магнітного поля утворюється за рахунок кінетичної енергії рухомих електричних
Під дією цієї ЕРС електрони почнуть упорядковано рухатися, виникне струм. Одночасно з цим виникає і магнітне поле. При цьому електрони в провіднику кола дістануть певну кінетичну енергію поступального руху вздовж електричного поля. Магнітне поле струму також набуде певного значення. До настання такого стаціонарного стану енергія електричного поля витрачалася на джоулеву теплоту і на збільшення кінетичної енергії електронів, тобто на створення магнітного поля струму.Щоб
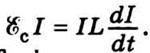Проте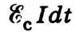 
– це робота за час dt. Отже, dА = LIdІ. Тоді
Величину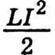 
називають власною енергією струму І в контурі з індуктивністю L. Збільшення сили струму в провіднику супроводжується підсиленням його магнітного поля. Тому природно допустити, що власна енергія струму є не що інше, як енергія його магнітного поля. Отже,
У цьому разі енергія поля виражена через параметри L та І, якими характеризується контур зі струмом. Бажано відшукати зв’язок енергії магнітного поля з параметрами, що характеризують саме поле: напруженість Н, магнітна індукція В та об’єм V простору, в якому зосереджене поле. Для цього розглянемо магнітне поле, яке створює соленоїд, що має на кожну одиницю довжини п витків і по якому проходить струм І. Нехай соленоїд, довжина якого l, має N витків. Тоді кількість витків пу що припадає на одиницю довжини, дорівнює відношенню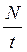 
. Визначимо енергію магнітного поля, що зосереджена в просторі, обмеженому соленоїдом. Використовуючи формулу (9.20), запишемо вираз для напруженості магнітного поля всередині соленоїда
Магнітний потік через один виток
Де s – площа витка. Магнітний потік через N витків
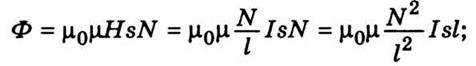
Де V = sl – об’єм соленоїда. Звідси можна визначити індуктивність соленоїда, виходячи з того, що Ф = LІ,
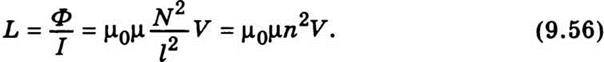
Виразивши силу струму через Н, матимемо
Підставивши значення I та L у (9.52), дістанемо
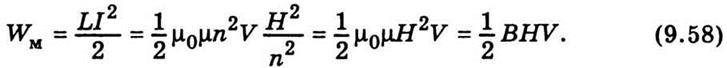
Отже, енергія магнітного поля, зосередженого в просторі об’ємом V, пропорційна напруженості поля і магнітній індукції. Виходячи з формули (9.58), неважко дістати вираз для густини енергії магнітного поля
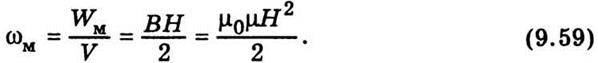
У загальному випадку для будь-яких магнітних полів (неоднорідних) густина ωм визначається так:
Енергію електромагнітного поля можна визначити як суму енергій електричного й магнітного полів:
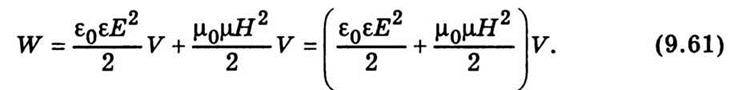
Звідси неважко визначити густину енергії електромагнітного поля
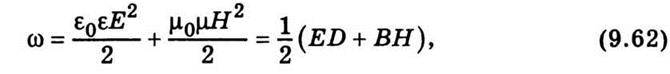
Де E – напруженість електричного поля; D – електрична індукція; В – магнітна індукція; Н – напруженість магнітного поля.
(1 votes, average: 5.00 out of 5)
Loading...