Гідродинаміка в’язкої рідини
ФІЗИКА
Частина 1 МЕХАНІКА
Розділ З ОСНОВИ МЕХАНІКИ СУЦІЛЬНОГО СЕРЕДОВИЩА
3.3. Гідродинаміка в’язкої рідини
В’язкість (внутрішнє тертя) – це властивість реальних рідин (газів) чинити опір переміщенню однієї частини рідини відносно іншої. При переміщенні одних шарів реальної рідини відносно інших виникають сили внутрішнього тертя, що спрямовуються по дотичній до поверхні шарів. Дія цих сил виявляється в тому, що з боку шару, який рухається швидше, на шар, який рухається повільніше, діє прискорювальна сила. І навпаки, з боку
Сила внутрішнього тертя F тим більша, чим більша виділена площа поверхні шару s (рис. 3.8), і залежить від зміни швидкості течії рідини при переході від шару до шару. На рис. 3.8 показано два шари, які розміщуються один від одного на відстані Δх і рухаються зі швидкостями 
1 і 2, при цьому 1 – 2 = Δ. Напрям, в якому відраховується відстань між шарами, перпендикулярний до швидкості течії шарів. Відношення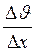 
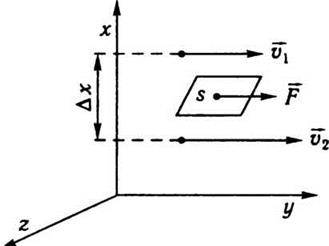
Рис. 3.8
Отже, модуль сили внутрішнього тертя
Де коефіцієнт пропорційності η, що залежить від природи рідини, називається коефіцієнтом динамічної в’язкості (або просто в’язкістю). В’язкість виражається в паскаль-секунд ах (Па∙с): один паскаль-секунда дорівнює коефіцієнту динамічної в’язкості середовища, в якому при ламінарній течії і градієнті швидкості з модулем, що дорівнює 1 м/с на 1 м, виникає сила внутрішнього тертя в один ньютон на 1 м2 поверхні дотику шарів (1 Па ∙ с = 1 Н ∙ с/м2). Чим більша в’язкість, тим більше рідина відрізняється від ідеальної, тим більші сили внутрішнього тертя в ній виникають. В’язкість залежить від температури, причому характер цієї залежності для рідин і газів різний: зі збільшенням температури в’язкість рідин зменшується, а газів, навпаки, збільшується. Це свідчить про різну природу в них механізмів внутрішнього тертя. Від температури особливо залежить в’язкість деяких масел. Наприклад, в’язкість касторового масла за температури 18…40 °С зменшується в чотири рази. Відомий фізик П. Л. Капиця (1894-1984) відкрив надтекучий стан рідкого гелію, в’язкість якого за температури 2,17 К дорівнює нулю.
Існує два режими течії рідин (газу). Течія називається ламінарною, якщо вздовж потоку кожний виділений тонкий шар сковзає відносно сусідніх, не переміщуючись з ними, і турбулентною (вихровою), якщо вздовж потоку відбуваються інтенсивне вихроутворення і перемішування рідини (газу). Ламінарна течія рідини спостерігається при відносно невеликих швидкостях її руху. Зовнішній шар рідини, що межує з поверхнею нерухомого твердого тіла, завдяки силам молекулярної взаємодії прилипає до неї і залишається нерухомим. Швидкість інших шарів буде тим більша, чим більша їх відстань від поверхні тіла.
При турбулентній течії частинки рідини мають складові швидкості, перпендикулярні до течії, тому вони можуть переходити з одного шару в інший. Швидкість частинок рідини тим більша, чим далі вони перебувають від поверхні тіла. Оскільки частинки рідини переходять із одного шару в інший, то їхні швидкості в різних шарах відрізняються мало. Завдяки великому градієнту швидкості біля поверхні тіла, як правило, утворюються вихори. Англійський учений О. Рейнольдс (1842-1912) установив, що характер течії залежить від безрозмірної величини, яку називають числом Рейнольдса:
Де ρ – густина рідини; – середня швидкість рідини; r – характерний лінійний розмір (наприклад, радіус труби, радіус кулі); ν =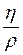 
– коефіцієнт кінематичної в’язкості.
При числах Рейнольдса, менших ніж 1000, спостерігається ламінарна течія, при великих – турбулентна. Крім того, число Рейнольдса може бути критерієм подібності для різних течій одного і того самого типу (наприклад, обтікання куль різного радіуса рідинами різної в’язкості). Течії, які можна одержати одну з іншої простою заміною масштабу вимірювання координат і швидкостей, називаються подібними. Можна сказати, що течії однакового типу з однаковим числом Рейнольдса подібні – у цьому полягає суть закону подібності.
Наведемо два характерних приклади ламінарної течії рідини.
Приклад 1. Розглянемо капіляр радіусом R і завдовжки l. У рідині подумки виділимо циліндричний шар радіусом r і завтовшки dr (рис. 3.9). У цьому разі з внутрішнього боку діє сила внутрішнього тертя, що визначається співвідношенням (3.9):
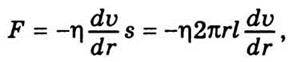
Де s = 2πrl – бокова поверхня циліндричного шару; знак ” мінус” означає, що при збільшенні радіуса швидкість зменшується з наближенням до стінки капіляра.
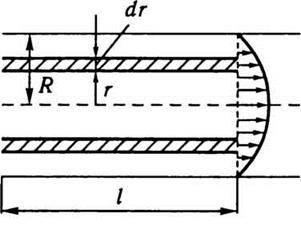
Рис. 3.9
Для усталеної течії рідини сила внутрішнього тертя врівноважується різницею тисків на кінцях циліндра
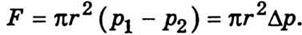
Звідси
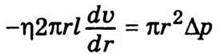
Aбо
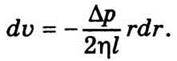
Припускаючи, що біля стінок відбувається прилипання рідини, тобто швидкість на відстані R від осі капіляра дорівнює нулю, після інтегрування дістанемо
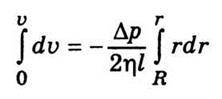
Aбо
Цей вираз уперше одержав Ж. Пуазейль (1799-1869). Вектори швидкості частинок рідини розподіляються за параболічним законом, причому вершина параболи лежить на осі капіляра.
За допомогою виразу (3.11) легко визначити об’єм рідини, що витікає з капіляра за час t:
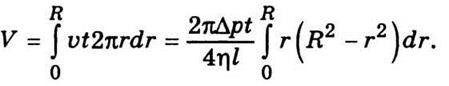
Звідси
Цю формулу прийнято називати законом Пуазейля.
Приклад 2. Розглянемо тепер повільний рух відносно малих кульок у рідині, коли їхні розміри значно менші, ніж розміри посудини, під дією сил тяжіння. На кульку, що падає в рідині вертикально вниз, діє три сили: сила тяжіння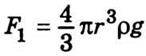 
(ρ – густина кульки, а r – її радіус); сила Архімеда 
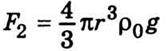(ρ0 – густина рідини) і сила опору, вираз якої емпірично встановив Дж. Стокс (1819-1903); 
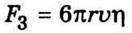(υ – швидкість кульки). При рівномірному русі кульки
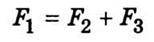
Або
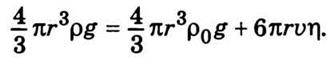
Після простих перетворень дістанемо
(1 votes, average: 5.00 out of 5)
Loading...