Комбінаторні задачі
Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ
§ 14. Комбінаторні задачі
Комбінаторика – розділ математики, який вивчає комбінації і перестановки предметів, розміщення елементів, що мають певні властивості тощо. Розглянемо задачу.
Задача 1. На пошті в продажу є 5 різних конвертів і 3 різні марки. Скількома способами можна купити конверт з маркою?
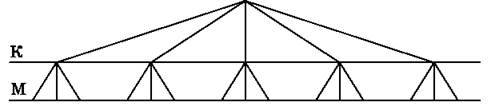
Рис. 5
Розв’язання. 1-й спосіб. Намалюємо дерево можливих варіантів (рис. 5). Позначимо конверт буквою К, марку – буквою М. Малюємо
Малюємо по 3 гілки. Рахуємо кількість отриманих внизу точок – 15 і отримуємо відповідь до задачі. Дерево можливих варіантів дає змогу розв’язувати різноманітні задачі, пов’язані з обчисленням кількості способів.
2-й спосіб. Оберемо конверт. У комплект до нього можна вибрати будь-яку з трьох марок. Тому є 3 комплекти, що містять обраний конверт. Оскільки конвертів усього 5, то кількість різних способів становить 15 (5 ∙ 3 = 15).
Дійшли до важливого правила комбінаторики – правила добутку:
Якщо
Правило добутку можна використовувати, якщо треба обрати більше 2 елементів.
Задача 2. На пошті в продажу є 5 різних конвертів, 3 різні марки і 4 різних вітальні листівки. Скількома способами можна купити комплект, що містить конверт, марку та листівку?
Розв’язання. 5 ∙ 3 ∙ 4 = 60 способів.
Розглянемо далі задачу, у якій треба полічити кількість способів, якими можна розмістити в ряд певну кількість предметів.
Задача 3. Дитина грається трьома іграшками: машиною, трактором, кораблем. Скількома способами їх можна викласти в ряд?
Розв’язання. На перше місце можемо поставити одну з трьох іграшок: машину, трактор або корабель. Після цього на друге місце можна поставити одну з двох наступних іграшок. Після цього на третє місце ставимо одну іграшку, яка залишилася після вибору перших двох. Використовуючи правило добутку, знайдемо, що іграшки можна розмістити шістьма різними способами (3 ∙ 2 ∙ 1). Перевіримо розв’язок задачі за допомогою дерева можливих варіантів (рис. 6).
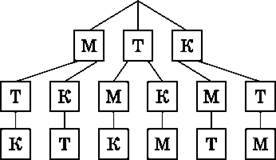
Рис. 6
Обчислили кількість способів, якими можна розмістити в ряд кілька предметів. Такі розміщення називають перестановками, вони відіграють велику роль у комбінаториці.
Позначають перестановки буквою Р. У задачі 3 кількість перестановок з трьох елементів дорівнює Р3 = 1 ∙ 2 ∙ 3; аналогічно кількість перестановок з двох елементів Р2 = 1 ∙ 2; із чотирьох елементів Р4 = = 1 ∙ 2 ∙ 3 ∙ 4 = 24; з п’яти Р5 = 1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 = 120 і т. д.
Розглянемо ще кілька комбінаторних задач.
Задача 4. З даних чисел вибрати такі, які при перестановці цифр утворюють числа, у яких число одиниць на 3 більше за число десятків: 42, 36, 74, 14, 85, 92, 47.
Розв’язання. Переставляючи цифри, маємо числа 24, 63, 47, 41, 58, 29, 74. Умову задовольняють числа 74 та 85.
Задача 5. В алфавіті племені БАБА є тільки дві літери “а” і “б”. Запиши всі слова цього племені, що містять: 1) дві літери; 2) три літери.
Розв’язання. 1) аа, ба, аб, бб (усього чотири слова); 2) ааа, ааб, аба, абб, ббб, бба, баб, баа (усього вісім слів). Зауважимо, що знайдена кількість слів узгоджується з правилом добутку. Оскільки на кожне місце є два “претенденти” – “а” і “б”, то слів, що містять дві літери, має бути 2 ∙ 2 = 4, а три літери – 2 ∙ 2 ∙ 2 = 8.
Розглянемо дві задачі на знаходження конфігурації елементів, що мають певні властивості.
Задача 6. У клітинки квадрата (рис. 7) треба поставити числа 1, 2, 3 та 4 так, щоб числа не повторювалися ні в рядках, ні в стовпчиках, ні по діагоналях (лініях, що ведуть з лівого нижнього кута в правий верхній та з правого нижнього кута в лівий верхній).
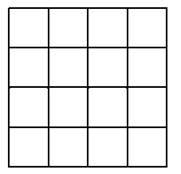
Рис. 7
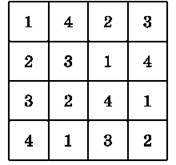
Рис. 8
Розв’язання. Один з варіантів розв’язання подано на рисунку 8.
Задача 7. Скількома способами можна розділити 5 цукерок між трьома дітьми так, щоб кожна дитина отримала хоча б по одній цукерці?
Розв’язання. Подамо розв’язок у вигляді таблиці. Отже, всього є 6 способів.
Спосіб | 1-ша дитина | 2-га дитина | 3-тя дитина |
1 | 3 | 1 | 1 |
2 | 1 | 3 | 1 |
3 | 1 | 1 | 3 |
4 | 2 | 2 | 1 |
5 | 2 | 1 | 2 |
6 | 1 | 2 | 2 |
Середній рівень
466. Які дві фігури (рис. 9) треба переставити місцями, щоб верхній рядок був таким, як нижній?
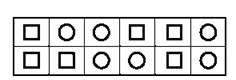
Рис. 9
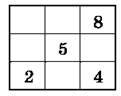
Рис. 10
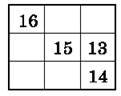
Рис. 11
467. Упиши в порожні клітинки (рис. 10) такі числа, щоб квадрат став “магічним”, тобто щоб суми чисел у кожному рядку, стовпці та по кожній діагоналі були однакові (спочатку знайди цю суму).
468. Заповни порожні клітинки (рис. 11) так, щоб квадрат став “магічним”, попередньо знайшовши суму чисел по діагоналі.
469. Костюм складається з блузки та спідниці. Скільки різних костюмів можна скласти з 5 видів блузок і
4 видів спідниць?
470. У танцювальному клубі займаються 7 юнаків і
9 дівчат. Скількома способами можна вибрати одну пару для участі в конкурсі?
471. У магазині є 7 видів ручок і 5 видів зошитів. Скількома способами можна дібрати комплект з однієї ручки й одного зошита?
472. Скількома способами можна дібрати пару з однієї голосної і однієї приголосної букви у слові “стежка”?
473. З міста А до міста В ведуть 3 дороги, а з міста В до міста С – 2 дороги (рис. 12). Скількома способами поштар Пєчкін може пройти з міста А в місто С?
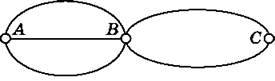
Рис. 12

Рис. 13
474. Кожну клітинку квадратної таблиці 2 х 2 (рис. 13) можна пофарбувати в зелений чи червоний колір. Скільки є різних варіантів розфарбувань цієї таблиці?
475. Скількома способами можна викласти в ряд червону, білу, чорну та зелену кульки?
476. З букв розрізної абетки складено слово “учень”. Скільки різних послідовностей букв можна отримати, переставляючи букви цього слова?
477. Скількома способами можна вишикувати в ряд чотирьох учнів?
478. Скільки існує двоцифрових чисел, у яких десятків не більше за 4, а одиниць не менше від 8?
479. Скільки існує двоцифрових чисел, у яких число десятків не менше від 7, а число одиниць не більше за 2?
480. Скільки різних трицифрових чисел можна написати цифрами:
1) 2, 5 і 5;
2) 0, 1 і 8?
481. Скільки різних чотирицифрових чисел можна написати цифрами 0, 2, 2, 5?
482. Запиши найбільше й найменше п’ятицифрове число, у яких сума цифр дорівнює 9.
483. Запиши найбільше і найменше чотирицифрові числа, у яких сума цифр дорівнює 8.
484. У магазині є книжки, які коштують 1 грн., 2 грн., 5 грн., 7 грн. і 8 грн. Учень має 10 грн. Які:
1) дві книжки;
2) три книжки він може купити, витративши всі гроші? Назви всі варіанти.
485. На вулиці гралося 12 дітей, причому хлопців було менше, ніж дівчат. Скільки надворі гралося хлопців і скільки дівчат? Назви всі варіанти.
486. Монету підкидають тричі. Скільки різних послідовностей випадання цифри та герба при цьому можна отримати?
Розв’язання. Перший раз може випасти цифра або герб (2 варіанти), другий раз – також 2 варіанти, третій раз – 2 варіанти. Отже, всього послідовностей буде 2 ∙ 2 ∙ 2 = 23 = 8.
487. Гральний кубик підкидають тричі. Скільки різних послідовностей чисел можна при цьому отримати?
488. Скільки різних трицифрових чисел можна скласти, використовуючи цифри 1 і 2, якщо цифри можуть повторюватися?
489. Скільки можна скласти різних чотирицифрових чисел, у запису яких є тільки непарні цифри (цифри можуть повторюватися)?
490. Скільки різних двоцифрових чисел можна скласти, використовуючи цифри 1, 2, 3, 4, 5, якщо цифри:
1) повторюються;
2) не повторюються?
491. У футбольній команді з 11 гравців треба вибрати капітана і його заступника. Скількома способами це можна зробити?
Розв’язання. Капітаном може бути будь-який з
11 гравців. Після вибору капітана на роль його заступника можуть претендувати 10 гравців, що залишилися. Таким чином (за правилом добутку), є 11 ∙ 10 = 110 різних варіантів.
492. Скількома способами можна вибрати старосту та його заступника в класі, у якому навчаються 28 учнів?
493. Скількома способами можна пошити двокольоровий прапор зі смужками однакової ширини, якщо є матеріал восьми різних кольорів?
494. З букв слова “сокіл” беруть деякі три і викладають у ряд. Скільки різних послідовностей букв при цьому можна отримати?
495. У мішку лежало 6 пар чорних і 6 пар білих рукавичок (усі вони переплутані). Яку найменшу кількість рукавичок необхідно взяти з мішка, не заглядаючи в нього, щоб скомплектувати хоча б одну пару однакових рукавичок?
496. У ящику лежать кульки трьох кольорів: білі, чорні та зелені. Яку найменшу кількість кульок, не заглядаючи в ящик, треба взяти, щоб серед них обов’язково було хоча б 4 кульки одного кольору?
497. Сполучи лініями два чи три числа (рис. 14), які в сумі становлять 100.
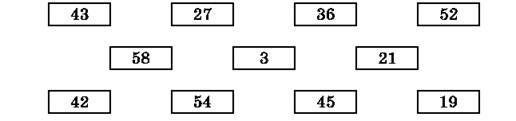
Рис. 14
498. Які два прямокутники (рис. 15) треба поміняти місцями, щоб сума чисел в обох стовпчиках зрівнялася? Знайди всі варіанти.
499. Запиши всі чотирицифрові числа, до запису яких входять лише цифри:
1) 0 і 1; 2) 1 і 2.

Рис. 15
500. Запиши всі трицифрові числа, до запису яких входять лише цифри:
1) 0 і 8; 2) 2 і 9.
501. Скільки існує двоцифрових чисел, у яких перша цифра менша від другої?
502. У кожній з 9 клітинок квадрата постав одне із чисел 4, 5, 6 так, щоб у кожному вертикальному та горизонтальному ряду числа не повторювались і щоб сума чисел, які стоять на кожній діагоналі, дорівнювала 15.
503. Постав у виразі 10 + 5 ∙ 7 – 3 одну пару дужок усіма можливими способами і знайди значення кожного виразу.
Високий рівень
504. Скількома способами можна заповнити одну картку в лотереї “Спортпрогноз”? (У цій лотереї треба передбачити підсумок одинадцяти спортивних матчів: перемогу однієї з команд або нічию; рахунок ролі не відіграє.)
505. Скільки різних трицифрових чисел можна скласти, використовуючи цифри 0, 1, 2, 3, 4, якщо цифри не повторюються?
506. Скільки існує трицифрових чисел, усі цифри яких парні й не повторюються?
507. Скільки є різних варіантів складання шифру, що містить чотири цифри, якщо цифри: 1) повторюються; 2) не повторюються?
508. Розклад на день містить 5 уроків. Визнач кількість можливих розкладів на один день, якщо в класі вивчається 9 предметів і предмети в розкладі не повторюються.
509. У країні Див 10 міст, кожні два з яких сполучено авіалінією. Скільки авіаліній у цій країні?
Розв’язання. Кожна авіалінія сполучає два міста. У ролі першого міста може виступати будь-яке з 10 міст, а в ролі другого – будь-яке з 9 міст, що залишилися. Перемножуючи, маємо 10 ∙ 9 = 90. Однак при цьому кожну з ліній враховано двічі. Тому всього авіаліній 90 : 2 = 45.
510. Під час зустрічі 8 чоловіків обмінялися рукостисканнями. Скільки рукостискань було здійснено?
511. У турнірі “Кубок Васюків” грає 12 шахістів, кожний з яких провів партію з кожним із суперників. Скільки було зіграно партій у цьому турнірі?
512. Скількома способами можна дібрати 2 олівці й 1 ручку з 5 різних олівців і 6 різних ручок?
Розв’язання. Перший олівець можна обрати 5 способами, а другий – 4 способами, бо один вже обраний. Але оскільки порядок вибору не має значення, то 2 олівці з 5 можна обрати (5 ∙ 4) : 2 = 10 різними способами. Одну ручку з 6 можна обрати 6 способами. Використовуючи правило добутку, всього маємо 10 ∙ 6 = 60 способів.
513. Скількома способами можна дібрати 2 марки і 2 конверти з 9 різних марок і 7 різних конвертів?
514. Три подружки разом купили 13 зошитів. Дві 3 них купили зошитів порівну (але більше одного). Скільки зошитів купила кожна з подружок? Розглянь усі варіанти.
515. Скільки є різних чотирицифрових чисел, сума цифр кожного з яких дорівнює 3?
516. Скільки існує різних семицифрових чисел, сума цифр кожного з яких дорівнює 2?
517. Алфавіт племені ПОТОП містить лише три літери: “П”, “О” і “Т”. Запиши всі слова цього племені, що містять:
1) дві літери; 2) три літери.
Вправи для повторення
518. Обчисли зручним способом:
1) 211 + 173 + 789; 2) 517 + 321 + 179 + 283;
3) 50 ∙ 17 ∙ 2; 4) 25 ∙ 11 ∙ 4 ∙ 7.
519. Знайди невідомі за рисунками (продуктивність праці обох робітників однакова):
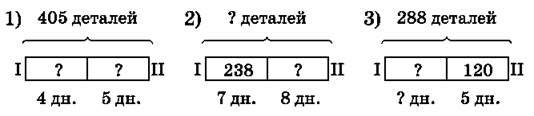
520. Маючи 12 грн., учень купив 3 олівці по 87 коп. та 2 ручки. Скільки коштує одна ручка, якщо учень отримав 2 грн. 19 коп. здачі?
521. Знайди невідоме слово за зразком: