Лінійчасті спектри
ФІЗИКА
Частина 5 АТОМНА ФІЗИКА
Розділ 15 БУДОВА АТОМА
15.3. Лінійчасті спектри
Будова спектрів атомів також суперечить законам класичної фізики. Виходячи з класичної електродинаміки, електрон, рухаючись по орбіті, повинен рівномірно випромінювати енергію, а тому атомний спектр має бути суцільним. Насправді спектр пари і газів, тобто практично ізольованих атомів, лінійчастий. Частоти ліній у спектрі пов’язані з будовою хімічних елементів. Спектри поглинання і випромінювання речовини взаємооборотні. Спектр кожного елемента
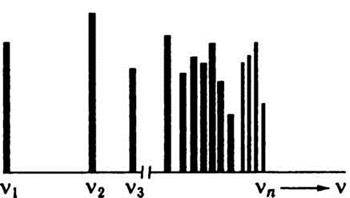
Рис. 15.3
У спектроскопії для характеристики спектральних ліній вводять величину, що дістала назву хвильового числа. Хвильове число ν’ дорівнює кількості довжин хвиль, що вміщується в 1 см. Отже,
Використання для характеристики спектральних ліній хвильового числа ν замість частоти ν’ пов’язано з тим,
Лінійчасті спектри різних елементів відрізняються один від одного. В більшості металів кількість ліній у цих спектрах дуже велика (у залізі, наприклад, понад 5000 ліній), а самі лінії мають різну інтенсивність.
Розглянемо спектр найпростішого атома – атома гідрогену. У видимій частині його найбільшу інтенсивність мають три лінії: червона, синьо-зелена і фіолетова; їх прийнято позначати символами Нα, Hβ, Нγ. Поряд з ними у видимій частині спектра є й інші лінії меншої інтенсивності. Є також чимало ліній в ультрафіолетовій та інфрачервоній ділянках спектра.
У 1885 р. швейцарський фізик Й. Бальмер установив, що довжини хвиль дев’яти відомих на той час ліній у спектрі гідрогену (ці лінії розміщуються у видимій частині спектра) можна визначити за
Де λ0 – стала величина, що дорівнює 364,613 нм, а λ для різних ліній серії набуває послідовно значень цілого ряду чисел, починаючи з трьох, тобто n = 3, 4, 5, 6,…________
Співвідношення (15.6) часто записують для хвильового числа
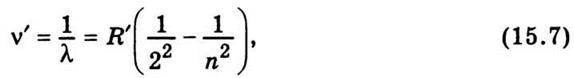
Де R’ = 10 973 731,53 м-1 – стала Рідберга; n = 3, 4, 5,… Якщо n = З, то ν’ точно збігається з хвильовим числом червоної гідрогенової лінії Нα, при n = 4 маємо хвильове число зеленої лінії Нβ і при n = 5 – хвильове число фіолетової лінії Нγ. Інші значення n точно визначають хвильові числа близько 30 ліній, спектроскопічно виявлених у видимій і близькій ультрафіолетовій частині спектра гідрогену, які утворюють так звану серію Бальмера. Зі збільшенням n дріб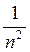 
зменшується і відповідно до формули (15.7) зменшується також різниця хвильових чисел двох сусідніх ліній. При досить великих n лінії надзвичайно тісно розміщуються одна біля одної. На рис. 15.4 схематично показано це поступове згущення ліній у спектрі гідрогену, наближення їх до межі, яка досягається при необмеженому зростанні n.
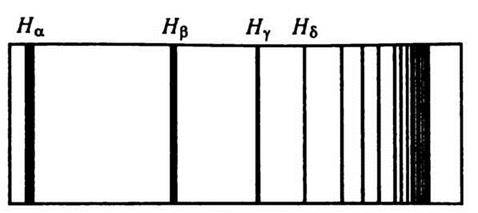
Рис. 15.4
Й. Рідберг показав, що в лінійчастих спектрах не лише гідрогену, а й інших елементів спостерігаються спектральні серії, причому частоти ν всіх ліній цієї серії задовольняють умову
Де l i n – цілі числа. Функції Т(i) і Т (n) називають спектральними термами. У межах цієї серії l є сталою величиною, а n змінюється.
У 1908 р. В. Рітц установив справедливість положення, яке називають комбінаційним принципом Рідберга – Рітца: частоти спектральних ліній випромінювання будь-якого атома можна представити як різницю двох термів. Здійснюючи різні комбінації термів, можна знайти всі можливі частоти спектральних ліній певного атома. Виходячи з комбінаційного принципу Рітца, слід чекати, що в спектрі гідрогену крім серії Бальмера є й інші серії. Наступні дослідження довели справедливість цього висновку. Частоти всіх ліній у спектрі атома гідрогену можна визначити за узагальненою формулою Бальмера:
Де R = R’c = 3,28984 ∙ 1015 с-1 також називають сталою Рідберга; l і n – цілі числа, причому n ≥ l + 1.
Значення l = 1 і n = 2,3,4,… відповідають серії Лаймана, яку знайдено в далекій ультрафіолетовій ділянці спектра; при l=2 і n = 3, 4, 5,… дістанемо серію Бальмера; l = 3, n = 4, 5, 6,… визначають серію Пашена в інфрачервоній ділянці спектра. В далекій інфрачервоній ділянці знайдено серію Брекета (l = 4, n = 5, 6,…), серію Пфунда (l = 5, n = 6, 7,…) і серію Хемфрі (l = 6, n = 7, 8, …).
Усі наведені формули емпіричні – це правила, за допомогою яких можна визначити частоти спектральних ліній для атома гідрогену. Проте з самого початку було зрозуміло, що ці правила мають глибокий фізичний зміст. Було зроблено спроби пояснити будову лінійчастих спектрів за допомогою класичної теорії внутрішньоатомних вібраторів. Теорію внутрішньоатомних вібраторів розробили X. Лоренц, П. Друде та ін. Вони виходили з уявлення, що всередині атома оптично активні електрони під дією електромагнітних хвиль світла приходять у гармонічний коливальний рух відносно деяких центрів рівноваги. На основі цієї моделі було пояснено експериментально встановлені закони поглинання й дисперсії світла. Вважали, що теорія внутрішньоатомних вібраторів, суміщена з ядерною моделлю атома, пояснить також походження лінійчастих спектрів. Однак проведені розрахунки довели неможливість навіть наближено розв’язати цю задачу таким способом.
Як уже згадувалось, із основних законів класичної електродинаміки випливає, що електрон, рухаючись по орбіті, має неперервно випромінювати енергію і при зменшенні своєї енергії наближатиметься до ядра. Отже, частота обертання ν0 і частота випромінювального світла мають поступово змінюватись.
Таким чином, якби класична електродинаміка, що знайшла своє підтвердження в численних дослідах у сфері макрофізичних процесів, була б справедливою і для внутрішньоатомних процесів, то спектр випромінювання атома складався б із серій ліній з частотами, кратними частоті обертання електрона навколо ядра (чого немає насправді). Сукупність великого числа атомів одного елемента випромінювала б суцільний спектр (тоді як випромінюється лінійчастий спектр). Унаслідок неперервних втрат енергії на випромінювання і спричинене цим наближення внутрішньоатомних електронів до ядра, всі атоми були б нестабільними. Насправді атомам властива виняткова стабільність і спектри, що характеризують їхню структуру, залишаються незмінними навіть при зіткненні атомів.
(1 votes, average: 5.00 out of 5)
Loading...