Рух зарядженої частинки в магнітному та електричному полях. Сила Лоренца
ФІЗИКА
Частина 3 ЕЛЕКТРИКА І МАГНЕТИЗМ
Розділ 9 МАГНЕТИЗМ. МАГНІТНЕ ПОЛЕ ЕЛЕКТРИЧНОГО СТРУМУ
9.6. Рух зарядженої частинки в магнітному та електричному полях. Сила Лоренца
Провідник, по якому проходить струм, відрізняється від провідника без струму тим, що в ньому відбувається впорядкований рух носіїв зарядів. Це наводить на думку про те, що сила, яка діє на провідник зі струмом, уміщений у магнітне поле, зумовлена дією сил на окремі рухомі заряди. А вже від цих зарядів дія передається провіднику, по якому вони переміщуються. Такий
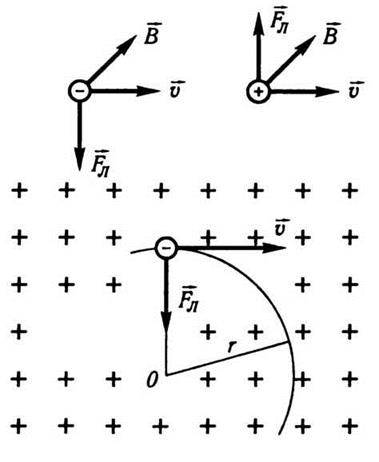
Рис. 9.7
Нехай електрон, що має швидкість 
, влітає в однорідне магнітне поле з індукцією 
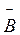, як показано на рис. 9.7. Лінії індукції магнітного поля позначені хрестиком і напрямлені від читача перпендикулярно до площини рисунка. Рухома заряджена частинка є електричним мікрострумом. Тоді для визначення сили, з якою магнітне поле діє на рухомий заряд е (е – заряд електрона), можна скористатися законом Ампера. За законом Ампера
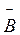діє з силою, що дорівнює IlBsin α (α – кут між напрямами поля і струму). Нехай рухомий заряд е за час t переміститься на відстань l. Це подібно до елемента струму, сила якого І = 
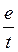. Підставивши цей вираз для І у формулу (9.21), дістанемо 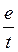LBsin α. Урахувавши, що у цьому разі sin α = l і l/t = υ, остаточно дістанемо вираз для сили Лоренца:
Для визначення напряму сили Лоренца можна застосувати правило лівої руки. Проте в цьому разі пальці потрібно розмістити не в напрямі руху електрона, а проти руху його, оскільки електрон заряджений негативно, а за напрям струму взято напрям руху позитивних зарядів. Скориставшись поняттям про векторний добуток, формулу (9.26) можна подати у такому вигляді:
Тоді співвідношення (9.27) одночасно зі значенням визначатиме і напрям сили, що діє в магнітному полі на рухомий електрон. Напрям сили, що діє в магнітному полі на позитивно заряджену частинку, збігається з напрямом векторного добутку, тобто
Формули (9.27) і (9.28) можна об’єднати
Але під q треба розуміти алгебраїчне значення заряду, що рухається (q > 0 для позитивних зарядів і q < 0 для негативних). На рис. 9.7 показано взаємне розташування векторів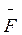 
Л, , 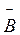для позитивного і негативного зарядів.
Оскільки сила Лоренца 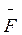Л завжди напрямлена перпендикулярно до швидкості руху зарядженої частинки, то вона не виконує роботи, а лише змінює напрям руху зарядженої частинки в магнітному полі. Абсолютне значення швидкості зарядженої частинки і кінетична енергія при цьому не змінюються. Сила Лоренца є доцентровою силою і надає зарядженій частинці доцентрового прискорення, що дорівнює 
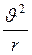, де υ – швидкість руху електрона; r – радіус кривизни траєкторії електрона в магнітному полі. Тоді, враховуючи перпендикулярність векторів i 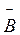, запишемо
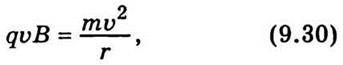
Де q – заряд частинки; m – її маса.
Із формули (9.30) видно, що траєкторія зарядженої частинки, яка влітає в однорідне магнітне поле (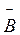 = const) під кутом 
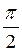до ліній магнітної індукції, має однакову кривизну, отже, є колом, радіус якого, виходячи з рівності (9.30), дорівнює
Якщо у просторі, де рухається заряджена частинка, створити магнітне поле, напрямлене під кутом α до її швидкості, то подальший рух частинки можна розглядати як геометричну суму двох рухів, що відбуваються одночасно, а саме: обертання по колу зі швидкістю υsinα у площині, перпендикулярній до силових ліній, та переміщення вздовж поля зі швидкістю υcosα. Отже, траєкторія частинки в цьому разі набуває форми гвинтової лінії, вісь якої паралельна напряму вектора 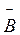(рис. 9.8).
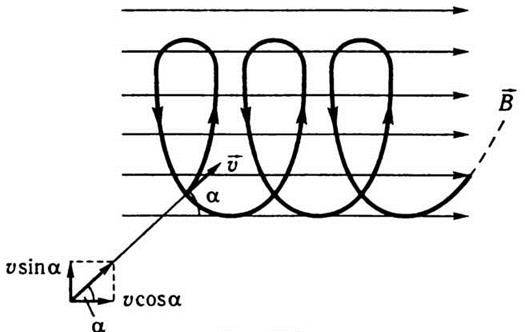
Рис. 9.8
Вплив електричного поля на рух електрона або іншої зарядженої частинки істотно відрізняється від впливу магнітного поля. Електричне поле змінює кінетичну енергію електрона, тоді як магнітне поле змінює тільки напрям руху, а не його швидкість. Рух зарядженої частинки, наприклад електрона, в електричному полі в загальному випадку подібний до руху тіла в гравітаційному полі: якщо початкова швидкість електрона протилежна напряму силових ліній однорідного електричного поля, то сила, що діє на нього, збігається з напрямом швидкості – електрон рухається рівноприскорено. При зворотному напрямі швидкості він рухатиметься рівносповільнено. Якщо початкова швидкість електрона перпендикулярна до напряму силових ліній однорідного електричного поля, то електрон рухатиметься по параболі.
Сила, що діє з боку однорідного електричного поля на електрон, який влітає в нього перпендикулярно до ліній напруженості, лише в початковий момент є доцентровою. Отже, радіус кривизни r такого електрона для початкової точки параболи можна обчислити зі співвідношення
Де Е – напруженість електричного поля; m – маса електрона. Таким чином, для електронів, що відхиляються поперечним електричним полем, радіус кривизни траєкторії пропорційний квадрату швидкості:
У загальному випадку на рухомий електричний заряд q може одночасно діяти магнітне поле з індукцією 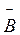і електричне поле, що характеризується напруженістю 
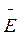. Тоді результуюча сила 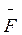, що діє на заряд, дорівнює векторній сумі сили 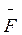Е = q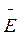, яка діє на заряд з боку електричного поля, і сили Лоренца 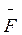Л = q :
Цей вираз називають формулою Лоренца. Згідно з (9.31) при відхиленні електрона магнітним полем радіус кривизни його траєкторії пропорційний першому степеню швидкості. Цю особливість використовують для вимірювання швидкості руху електронів методом взаємної компенсації дії електричного й магнітного полів на рух електрона.
Якщо розмістити плоскі полюси електромагніта так, щоб магнітні силові лінії були перпендикулярні до силових ліній електричного поля і потік електронів проходив одночасно між полюсами електромагніта і пластинами плоского конденсатора, то, регулюючи силу струму в обмотці електромагніта (змінюючи індукцію магнітного поля), відхилення електронів від прямолінійного шляху, спричинене електричним полем, можна повністю компенсувати однаковим за значенням, але протилежним за напрямом відхиленням, спричиненим магнітним полем. Із формул для радіусів кривизни траєкторії електронів у поперечному електричному (9.33) і магнітному (9.31) полях видно, що відхилення можна взаємно компенсувати, якщо
Виконується співвідношення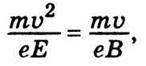 
Або
Ця формула дає змогу визначити швидкість заряджених частинок (електронів) вимірюванням напруженості електричного й індукції магнітного полів, підібраних так, щоб їхні відхильні дії взаємно компенсувались. Якщо після цього усунути електричне поле і виміряти відхилення електронів у магнітному полі, то за r, Е і В можна визначити питомий заряд електрона – відношення заряду електрона до його маси. Формулу для обчислення цього відношення можна дістати із (9.31) і (9.35):
Питомий заряд електрона був уперше визначений Дж. Томсоном. На основі вимірювань відхилення катодних променів у електричному і магнітному полях було встановлено, що
Ураховуючи, що елементарний заряд е = 1,602 ∙ 10-19 Кл, і знаючи е/m, дістанемо, що маса електрона m = 9,109 ∙ 10-31 кг.
Розглянутий метод визначення е/т, можна застосовувати тоді, коли всі частинки в потоці мають однакову швидкість. Усі електрони, що утворюють пучок, прискорюються однією і тією самою різницею потенціалів, яку прикладено між катодом, з якого вони вилітають, і анодом; тому розкид значень швидкостей електронів у потоці дуже малий.
Позитивні іони утворюються за рахунок іонізації молекул газу. Виникаючи в різних місцях, іони долають неоднакову різницю потенціалів, унаслідок чого швидкості різних іонів відрізняються одна від одної. Тому метод, за допомогою якого було визначено питомий заряд електронів, не можна застосовувати до іонів.
У 1907 р. Дж. Томсон розробив “метод парабол”, за допомогою якого можна визначити питомий заряд іонів.
Виконавши дослід з хімічно чистим неоном, Дж. Томсон з’ясував, що цей газ утворював дві параболи, які відповідають атомним масам 20 та 22. Спроби пояснити цей результат привели до припущення про існування двох хімічно неподільних різновидів атомів неону (за сучасною термінологією – два ізотопи неону). Довів це припущення Ф. Астон, який удосконалив метод визначення питомого заряду іонів. Прилад, за допомогою якого можна визначити е/m різних іонів, Ф. Астон назвав мас-спектрографом.
(1 votes, average: 5.00 out of 5)
Loading...