Способи задання функції
789. 1) Аргумент t, залежна змінна s;
2) аргумент x, залежна змінна у;
3) аргумент а, залежна змінна V;
4) аргумент x, залежна змінна f.
790. у = 10x + 1
1) Якщо x = -1, то у = 10 • (-1) + 1 = -9.
2) Якщо x = 3, то у = 10 • 3 + 1 = 31.
3) Якщо х = -1/5, то y = 10 • (-1/5) + 1 = -1.
4) Якщо x = 7, то у = 10 • 7 + 1 = 71.
791. у = х2 – 3
1) Якщо x = 5, то у = 52 – 3 = 22.
2) Якщо x = -4, то у = (-4)2 -3 = 13.
3) Якщо x = 0,1, то у = 0,12 – 3 = 0,01 – 3 = -2,99.
4) Якщо x = 0, то у = 02 – 3 = -3.
792. 1) y = -1/6x + 2
X | 12 | 6 | -6 |
Y | 0 | 1 | 3 |
0 | 1 | 2 | -4 | -3 |
2 |
|
|
|
|
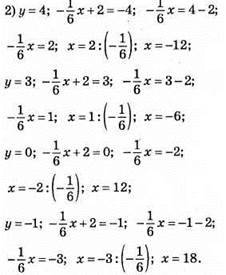
793. f(x) = 3 – 4x
1) f(-2) = -5 – рівність неправильна;
F(-2) = 3 – 4 • (-2) = 11;
2) f(1/2) = 1 – рівність правильна;
F(1/2) = 3 – 4 • 1/2 = 3 – 2 = 1;
3) f(0) = -1 – рівність неправильна;
F(0) = 3 – 4 • 0 = 3;
4) f(-1) = 7 – рівність правильна;
F(-1) = 3 – 4 • (-1) = 3 + 4 = 7.
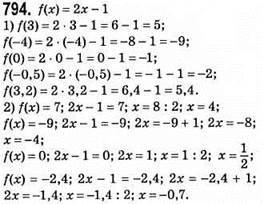
3) f(5)
F(0,3) = 0,4 – рівність неправильна, бо f(0,3) = 2 • 0,3 – 1 = -0,4;
F(-3) = -7 – рівність правильна, бо 2 • (-3) – 1 = -7.
795. у = х(х + 8)
X | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
Y | -15 | -12 | -7 | 0 | 9 | 20 | 33 |
796. у = -2/3х
X | -9 | -6 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 6 |
У | 6 | 4 | 2 |
| 2/3 | 0 | -2/3 |
| -2 | -4 |
797. 1) Функцію задано описом.
2) Область значень цієї функції шість чисел: 0, 1, 2, 3, 4, 5.
3)
X | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
Y | 5 | 0 | 1 | 2 | 3 | 4 | 5 | 0 | 1 |
798. 1) Функцію задано описом.
2) у = 2x
X | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
У | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
799. 1) у = – х; 2) у = 3х; 3) у = х2 + 4.
800. 1) у = х – 3; 2) у = 2x + 5.
801. у = х2 + 2х, де -1 ≤ х ≤ 3.
X | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
Y | -1 | -0,75 | 0 | 1,25 | 3 | 5,25 | 8 | 11,25 | 15 |
802. y = х3 – 1, де -3 ≤ х ≤ 2.
X | -3 | -2 | -1 | 0 | 1 | 2 |
Y | -28 | -9 | -2 | -1 | 0 | 7 |
803. у = 0,2х – 5.
X | 4 | 35 | -1,5 | 18 | -3 |
У | -4,2 | 2 | -5,3 | -1,4 | -5,6 |
804. у = 8 – 1/7х.
X | 14 | 56 | -1,4 | -7 |
У | 6 | 0 | 8,2 | 9 |
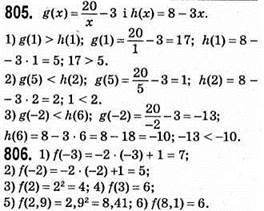
807. 1) Якщо х = 3, то у = -2 • 3 + 4 = -2.
2) Якщо x = 0,001, то у = -2 • 0,001 + 4 = -0,002 + 4 = 3,998.
3) Якщо х = 0, то у = 0,1 • 0 – 5 = -5.
4) Якщо х = -8, то у = 0,1 • (-8) – 5 = -0,8 – 5 = -5,8.
808. 1) Область визначення складають числа: 2, 4, 6, 8, тобто одноцифрові парні натуральні числа;
2) у = х + 3. Кожному натуральному одноцифровому числу поставили у відповідність число, на 3 більше відповідного значення аргументу.
809. 1) Область визначення складають одноцифрові натуральні непарні числа: 1, 3, 5, 7, 9.
2) Кожному натуральному непарному одноцифровому числу поставили у відповідність число вдвічі менше відповідного значення аргументу. y = x/2.
810. х2 – 8х = 4 – 8х; х2 – 8х + 8х = 4; х2 = 4; (х – 2)(х + 2) = 0; х – 2 = 0; х = 2 або х + 2 = 0; х = -2.
При х = 2 або х = -2 функції набувають рівних значень.
811. 3x + 5 = x; 3х – х = -5; 2х = -5; х = -5 : 2; x = -2,5.
При х = -2,5 значення функції дорівнює значенню аргументу.
812. x2 + 2x – 1 = 2x; x2 + 2x – 2x = 1; x2 = 1; (х – 1)(x + 1) = 0; х – 1 = 0; х = 1 або х + 1 = 0; х = -1.
При х = 1 і при х = -1 значення функції дорівнює подвоєному значенню аргументу.
813. f(3,7) = 3; f(0,64) = 0; f(2) = 2; f(0) = 0; f(-0,35) = -1; f(-2,8)= -3.
814. 1) 3,4(1 + 3x) – 1,2 = 2(1,1 + 5,1x); 3,4 + 10,2х – 1,2 = 2,2 + 10,2х; 10,2х – 10,2х = 2,2 + 1,2 – 3,4; 0 • х = 0; рівняння має безліч коренів.
2) |2x – 1| = 17,3;
2x – 1 = 17,3; 2х = 17,3 + 1; 2х = 18,3; x = 18,3 : 2; x = 9,15;
Або 2x – 1 = -17,3; 2x = -17,3 + 1; 2x = -16,3; x = -16,3 : 2; x = -8,15.
Рівняння має два корені.
3) 3(|x – 1| – 6) + 21 = 0; 3|x – 1| – 18 + 21 = 0; 3|x – 1| + 3 = 0; 3|x – 1| = -3; |x – 1| = -3 : 3; |x – 1| = -1; рівняння не має жодного кореня.
4) 0,2(7 – 2x) = 2,3 – 0,3(x – 6); 1,4 – 0,4x = 2,3 – 0,3x + 1,8; -0,4x + 0,3x = 2,3 + 1,8 – 1,4; -0,1x = 4,1 – 1,4; -0,1x = 2,7; x = 2,7 : (-0,1); x = -27; рівняння має один корінь.
815. Нехай x, x – 10, x + 10 – дані три числа. За умовою
X(x + 10) – 320 = (x + 10)(x – 10); x2 + 10x – 320 = x2 + 10x – 10x – 100; 10x = 320 – 100; x = 22; x – 10 = 12; x + 10 = 32.
12; 22; 32 – шукані числа.
816. а + с = 2b, а = 2b – с, тоді а2 + 8bc = (2b + c)2; (2b – c)2+ 8bс = (2b + с)2; 4b2 – 4bс + с2 + 8bс = (2b + с)2; 4b2 + 4bс + с2 = (2b + с)2 – правильна рівність, отже, коли а + с = 2b, то а2+ 8bс = (2b + с)2.
817. x + у = a2/4; у + z = – а; x + z = 1.
Додамо почленно дані рівності:
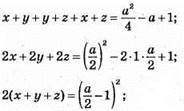
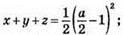
Оскільки вираз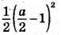 
набуває тільки невід’ємних значень, то x + у + z набуває тільки невід’ємних значень.
818.
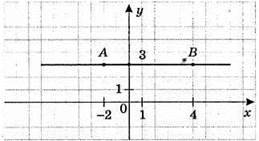
Ординати точок цієї прямої дорівнюють 3.
819.
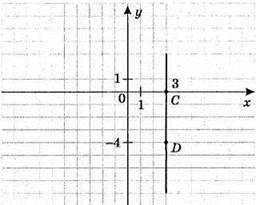
Абсциси точок цієї прямої дорівнюють 3.
(1 votes, average: 5.00 out of 5)
Loading...