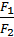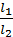Умова рівноваги важеля
Розділ IV МЕХАНІЧНА РОБОТА ТА ЕНЕРГІЯ
&46. Умова рівноваги важеля
✓ Які пристрої називають простими механізмами?
✓ Яка будова і принцип дії важільних ваг?
1. Ознайомимося докладніше з одним із найпоширеніших простих механізмів – важелем. Для того, щоб довгий стержень перетворився на важіль, він повинен мати можливість обертатися навколо нерухомої опори або осі.
На рисунку 141 важелем являється лом, який може обертатися навколо осі О обертання – лінії, перпендикулярної до повздовжньої осі важеля. Якщо на довгий кінець
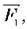його короткий кінець піднімає тягар, що діє на нього з силою 
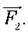Точки прикладання цих силзнаходяться на протилежних відносно точки О боках важеля.Точка прикладання сили – це точка, в якій на важіль діє інше тіло.
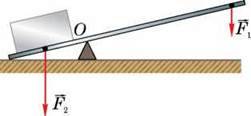
Рис. 141
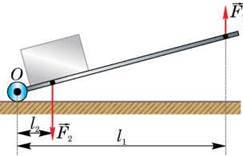
Рис. 142
На рисунку 142 показано, як принцип дії важеля використовується в роботі візка (див. рис. 138, б). Людина діє з силою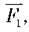 
піднімаючи візок і вантаж, що знаходиться в ньому. Нерухома точка опори важеля – точка О і вісь його обертання
В обох випадках використання важеля дає виграш у силі. Чи можна підрахувати цей виграш? Чи існує якась закономірність, що дає змогу розрахувати величину сили, яку потрібно прикласти, щоб підняти вантаж за допомогою важеля? Чи можна визначити місце прикладання сили, наприклад, м’язового зусилля, потрібного для піднімання вантажу?
Щоб відповісти на ці запитання, проробимо дослід. До важеля, який може обертатися навколо осі О, підвісимо тягарі з різною масою (рис. 143). Тягарі розміщуються по різні боки від осі О і діють на важіль із силами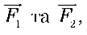 
напрямленими вертикально вниз. Важіль і діючі на нього сили схематично показані на рисунку 144. Зафіксуємо положення більшого тягаря в точці А. Залежно від місця закріплення меншого тягаря важіль може розпочати обертання за годинниковою стрілкою або проти її ходу. І лиш тільки цей тягар буде закріплено у точці В, важіль перебуватиме у рівновазі.
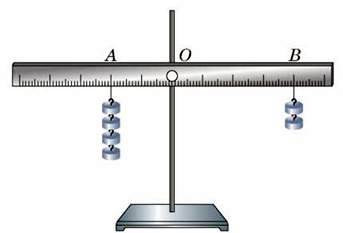
Рис. 143
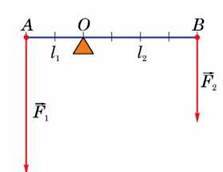
Рис. 144
Отже, за заданих значеннях сил F1 і F2 співвідношення відстаней від осі обертання до точок прикладання цих сил (ОА і ОВ) будуть строго визначеними. Оскільки у цьому досліді сили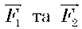 
– це ваги тягарів, і вони відповідно рівні силам тяжіння, що діють на тягарі з масами 400 г і 200 г (4 і 2 гирі з масами по 100 г кожна), то сила 
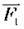удвічі більша за силу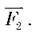 
Як показують вимірювання, відстань ОА виявляється вдвічі меншою від відстані ОВ.
Змінимо умови досліду і прикріпимо в точці А тягар, у 3 рази більший, ніж тягар у точці В. Виявиться, що для приведення важеля в рівновагу менший тягар доведеться змістити на відстань у 3 рази більшу, ніж відстань ОА. Щоб описати помічену закономірність, доведеться ввести поняття плеча сили.
Плече сили – це найкоротша відстань від осі обертання тіла до лінії дії сили.
Щоб знайти плече сили, треба опустити перпендикуляр з точки опори на лінію, вздовж якої діє сила.
На рисунках 142 і 144 плечем сили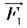 
є відстань l1 (OA) – перпендикуляр, опущений з точки О на пряму, вздовж якої діє сила
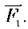Відповідно плечем сили 
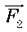є відстань l2 (OB).
На основі подібних дослідів більше двох тисяч років тому давньогрецьким ученим Архімедом було встановлене правило: важіль перебуває у рівновазі, якщо сили, що діють на нього, обернено пропорційні плечам цих сил.
Це правило (умова) рівноваги важеля можна записати у вигляді формули:
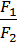, або F1l1 = F2l2,
Де F1 і F2 – сили, що діють на важіль, l i l2 – відповідно плечі цих сил.
Знаючи правило рівноваги важеля, можна зрозуміти, як за допомогою важеля можна одержати виграш у силі. Якщо до кінця довшої частини важеля прикласти певну невелику силу, то нею можна зрівноважити значно більшу силу, прикладену до коротшої його частини.
Добуток сили на її плече називають моментом сили. Одиниця моменту сили – ньютон-метр (1 Н ∙ м). Увівши момент сили і прийнявши до уваги останню формулу, можна дещо інакше сформулювати правило рівноваги важеля: важіль перебуває у рівновазі, якщо момент сили, що обертає його за годинниковою стрілкою, дорівнює моменту сили, що обертає важіль проти годинникової стрілки.
Як можна пояснити виграш у силі у прикладі з візком (див. рис. 142), використавши правило рівноваги важеля?
Сили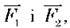 
які діють на візок, паралельні одна одній і напрямлені у протилежні боки. Сила 
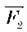прагне обертати важіль відносно осі О за годинниковою стрілкою, а сила 
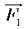– проти її ходу. Плечі сил 
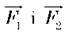відповідно дорівнюють l1 i l2 Згідно з правилом рівноваги важеля плече завдовжки l2 набагато менше від плеча l1 . Отже, щоб зрівноважити важіль, сила F1 може бути значно меншою за силу F2. Так що виграш у силі очевидний.
У багатьох машинах і механізмах, які знайшли широке використання у техніці й побуті, застосовуються важелі. Ви уже знайомі з будовою і принципом дії важільних ваг. Вони саме так і називаються – “важільні ваги”, тому що їхній основний елемент – важіль.
Розглянемо уважніше звичайні ножиці (рис. 145). Вони являють собою пару важелів, скріплених у точці О. Відносно осі, що проходить через цю точку, вони можуть обертатися. Будемо вважати, що важіль CD залишається у спокої, а до кінця важеля АВ прикладається сила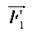 
– сила з бокупальців людини, що працює з ножицями. Сила 
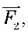яка діє з боку аркуша паперу на важіль, виявиться набагато більшою, ніж прикладена сила 
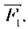На тому самому принципі заснована робота й інших інструментів: щипців, плоскогубців, садового секатора тощо.
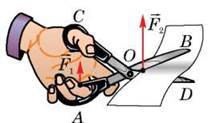
Рис. 145
Важіль часто зустрічається в живій і неживій природі. Пояснюючи, наприклад, причину падіння дерев під час бурі, доведеться згадати про правило рівноваги важеля. Сила опору грунту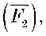 
яка діє на корені дерева (рис. 146), у деякий момент може виявитися недостатньою для того, щоб утримати дерево в рівновазі, і воно впаде під напором пориву вітру 
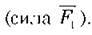В організмах людей і тварин, у тілах птахів і комах багато важелів. Тільки у вашому тілі більше 200 різних кісткових важелів. Досить цікавий висновок можна зробити, розглянувши дію важеля у ліктьовому суглобі людини (рис. 147). У цьому важелі точка опори (О)
Знаходиться всередині суглоба. Вага тягаря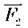 
прикладена до кінця важеля, а сила 
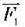виникає внаслідок скорочення м’язів руки людини.
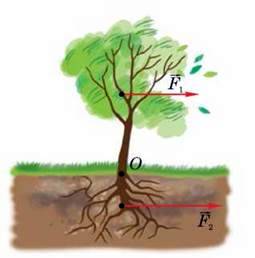
Рис. 146
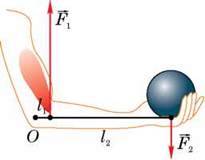
Рис. 147
Згідно з правилом рівноваги важеля сила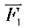 
повинна набагато перевищувати силу 
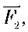оскільки плече l1, набагато менше від плеча l2. Тут важіль дає програш у силі, але виграш у відстані. Виявляється, сила м’язів руки людини значно більша за вагу тягаря, який вона піднімає.
Запитання для самоперевірки
1. У чому полягає правило рівноваги важеля?
2. Що називають плечем сили?
3. Що таке момент сили? В яких одиницях він вимірюється?
4. Наведіть різні формулювання правила рівноваги важеля.
5. Поясніть дію важеля на якому-небудь прикладі.
6. Чи можна правило рівноваги важеля назвати законом? Відповідь обгрунтуйте.
Завдання 35
1. Поясніть, чому дверну ручку прикріплюють біля краю дверей, а, наприклад, не посередині.
2. На рисунку 148 зображені кусачки, залізничний шлагбаум, гальмівна педаль автомобіля і підйомний кран. Укажіть точки опори і плечі сил у цих важелів. В яких випадках ці механізми використовуються для отримання виграшу в силі, а в яких – для виграшу у відстані?
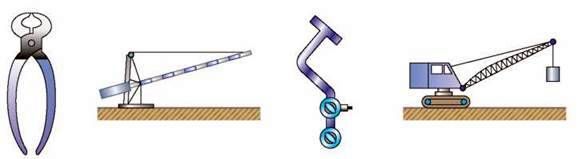
Рис. 148
3. З якою масою тягар треба підвісити до короткого плеча важеля у точці А (рис. 149), якщо до довгого плеча у точці В прикріплені два тягарі, які діють на важіль із силами 1 Н кожний?
4. Поясніть принцип дії автонапувалки, зображеної на рисунку 150, де 1 – чашка автонапувалки, 2 – педаль, 3 – труба, що підводить воду з водогону, 4 – клапан, 5 – пружина.
5. Сила, з якою рука людини стискає щипці, дорівнює 120 Н. Відстань від точки опори до стискуваного щипцями цвяха 1,5 см, а від точки опори до точки прикладання сили 15 см. З якою силою діють щипці на цвях?
6. До балки, яка лежить на двох опорах А та В (рис. 151) підвішений вантаж із масою 500 кг. Відстань від точки підвісу вантажу до одного з кінців балки в 4 рази більша, ніж до другого. З якою силою тисне балка на кожну опору?
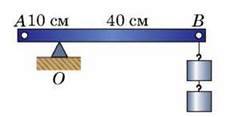
Рис. 149
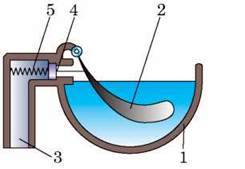
Рис. 150
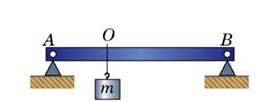
Рис. 151
7. До кінців легкого стержня завдовжки 1 м підвішені дві кулі з масами 50 г і 200 г. На якій відстані від кулі з більшою масою треба підперти стержень, щоб він перебував у рівновазі?
Робота з комп’ютером
Вивчіть матеріали уроку і виконайте завдання, запропоновані в електронному додатку.
Лабораторна робота № 11
Вивчення умови рівноваги важеля
Мета роботи. 1. Навчитися визначати момент сили. 2. Перевірити на досліді правило рівноваги важеля.
Обладнання. 1. Шкільний лабораторний важіль. 2. Штатив. 3. Набір важків масою по 100 г. 4. Динамометр. 5. Лінійка (мірна стрічка).
Хід роботи
1. Удома заздалегідь повторіть &46 підручника.
2. Закріпіть важіль у штативі і зрівноважте його в горизонтальному положенні, обертаючи гайки на кінцях важеля.
3. У першому досліді зліва на відстані 20 см від осі обертання важеля закріпіть один важок із масою m1 = 100 г. При цьому на важіль з боку важка діятиме сила F1 що є вагою важка, причому F1 = P1 = m1g. Дані цього вимірювання і наступні заносьте у звітну таблицю.
4. Справа до важеля прикріпіть два таких самих важки і, пересуваючи підвіс уздовж важеля, досягніть такого положення рівноваги, щоб важіль перебував у горизонтальному положенні. Сила F2 = Р2 = m2g, де m2 = 200 г. Виміряйте плечі сил l1 і l2.
5. У другому досліді перемістіть важок зліва ближче до осі обертання або далі від неї і знайдіть положення важків на правій частині важеля, при якому він перебуватиме у горизонтальному положенні рівноваги. Виміряйте плечі сил.
6. У третьому досліді до лівого плеча важеля на відстані 10-20 см від осі обертання підвісьте три важки з масою по 100 г, а до правого – у довільній точці прикріпіть динамометр. Розтягаючи пружину динамометра вертикально вниз, досягніть горизонтального положення рівноваги важеля. Зніміть показ динамометра і виміряйте плечі сил.
7. Додаткове завдання. Перевірте правило рівноваги важеля для випадку, коли обидві сили діють на важіль з одного боку по відношенню до осі його обертання. Використовуйте важки і динамометр. Виміряйте плечі сил і обчисліть їхні моменти. Зробіть відповідний висновок.
8. Результати вимірювань занесіть у таблицю і проведіть відповідні розрахунки.
Ліва частина важеля | Права частина важеля | |||||||||
№ досліду | Маса важкаm1, кг | Сила F1 = m1g, H | Плече силиl1, м | Момент сили М1 +F1l1,Hм | Маса важкаm2, кг | СилаF2 =m2g, Hпоказ динамометр | Плече силиl2, м | Момент сили М2 +F2l2,Hм | Відношення сили | Відношення сили |
1. | ||||||||||
2. | ||||||||||
3. | – | |||||||||
4. | – |
(1 votes, average: 5.00 out of 5)
Loading...