Відсоткові розрахунки. Формула складних відсотків
УРОК № 42
Тема. Відсоткові розрахунки. Формула складних відсотків
Мета уроку: закріпити знання учнів про формули розв’язування основних задач на відсотки. Продовжити роботу над виробленням умінь застосовувати вивчені формули для розв’язування задач на відсоткові розрахунки. Повторити розв’язання задач на складання та розв’язування математичних моделей.
Тип уроку: закріплення знань, відпрацювання вмінь.
Наочність та обладнання: опорний конспект № 24.
Хід уроку
I. Організаційний етап
Учитель перевіряє
II. Перевірка домашнього завдання
На цьому етапі уроку можна провести роботу з перевірки домашнього завдання за зразком або перевірити рівень засвоєння основних знань та вмінь учнів на попередньому уроці, запропонувавши їм виконати тестові завдання (див. нижче).
Тестові завдання
Варіант 1
1. Скільки відсотків години становлять 42 хвилини?
А) 24%; б) 42%; в) 70%; г) 170%.
2. Вміст цукру в яблуках становить 9,6%. Скільки кілограмів цукру міститься у 25 кг таких яблук?
А) 24 кг; б) 2,4 кг; в) 38,4 кг; г) 3,84 кг.
3. Ціну на товар знизили на 10%, і він став коштувати 432 грн.
А) 4320 грн; б) 480 грн; в) 442 грн; г) 475,2 грн.
4. Вкладник поклав до банку 20 000 грн під 10 % річних. Скільки гривень буде в нього на рахунку через 2 роки?
А) 20100 грн; б) 21000 грн; в) 24200 грн; г) 22000 грн.
Варіант 2
1. Скільки відсотків години становлять 48 хвилин?
А) 80%; б) 48%; в) 8%; г) 84%.
2. У сплаві міді з оловом 40 % становить мідь. Скільки кілограмів міді містить шматок такого сплаву масою 8 кг?
А) 50 кг; б) 5 кг; в) 3,2 кг; г) 32 кг.
3. Ціну на товар підвищили на 10%, і він став коштувати 495 грн. Якою була початкова ціна товару?
А) 4950 грн; б) 544,5 грн; в) 45 грн; г) 450 грн.
4. Вкладник поклав до банку 10 000 грн під 20 % річних. Скільки гривень буде в нього на рахунку через 2 роки?
А) 10400 грн; б) 40000 грн; в) 14000 грн; г) 14 400 грн
III. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів
Оскільки на попередньому уроці було розглянуто найпростіші задачі на відсотки, то цілком логічно на даному уроці продовжити роботу з формування вмінь розв’язувати задачі на відсоткові розрахунки більш високого рівня складності. Отже, основна мета даного уроку полягає в тому, щоб закріпити знання учнів про формули розв’язування задач на відсотки, а також продовжити роботу над виробленням умінь виконувати дії відповідно до цих формул.
IV. Актуалізація опорних знань та вмінь учнів
Усні вправи
1. Знайдіть:
1) 25% від числа 28;
2) 40% від числа 30;
3) 125% від числа 36.
2. Знайдіть;
1) число, 20% якого дорівнює 18;
2) число, 60% якого дорівнює 120.
3. Знайдіть, скільки відсотків становить:
1) число 7 від числа 35;
2) число 24 від числа 32.
4. Вкладник поклав до банку 1000 грн під 20% річних. Поясніть відповідно до цієї умови зміст виразу:
1) 1000 ? 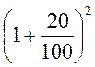 ;
;
2) 1000 ? 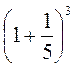 .
.
V. Відпрацювання вмінь
Письмові вправи
Для розв’язування на уроці пропонуються вправи такого змісту:
1) задачі на відшукання відсотків від числа;
2) задачі на відшукання числа за заданим значенням його відсотків;
3) задачі на відшукання відсоткового відношення двох чисел;
4) задачі на застосування формули складних відсотків.
Методичний коментар
Як було сказано вище, серед задач, які мають бути розв’язані на даному уроці, є задачі, що описують ті самі ситуації, що і на попередньому уроці, хоча мають більш високий рівень складності.
Для кращого закріплення знань учнів та свідомого виконання дій при розв’язанні всіх запропонованих вправ бажано вимагати від учнів коментарів, що спираються на вивчені формули відсоткових розрахунків.
VI. Підсумки уроку
Контрольні запитання
1. Що називають відсотком від числа?
2. Як знайти а% від числа b? Наведіть приклад.
3. Як знайти число, якщо а% від цього числа дорівнює b? Наведіть приклад.
4. Як знайти, скільки відсотків становить одне число від іншого? Наведіть приклад.
5. Як знайти нарощений через х років капітал А, якщо відсоткова ставка становить b%, а початковий внесок становив с грн?
VII. Домашнє завдання
1. Повторити формули розв’язування задач на відсоткові розрахунки.
2. Виконати самостійну роботу (див. нижче) за варіантом, указаним учителем.
3. На повторення: поняття випадкової події, ймовірність випадкової події (6 клас).
Самостійна робота
Варіант 1
Розв’яжіть задачі.
1) В автопарку було 200 машин, 115 з яких – вантажівки. Скільки відсотків усіх машин автопарку є вантажними?
2) Вкладник поклав до банку 10000 гривень під 14% річних. Скільки грошей буде на його рахунку через 2 роки?
3) Вартість деякого товару спочатку підвищили на 20%, а потім знизили на 20 %. На скільки відсотків і як змінилась початкова ціна товару?
4) Підприємець взяв кредит у банку в розмірі 30 000 гривень під деякий відсоток річних. Через два роки він повернув до банку 43 200 гривень. Під який відсоток річних дає кредити цей банк?
Варіант 2
Розв’яжіть задачі.
1) В автопарку було 300 машин, 105 з яких легкові. Скільки відсотків усіх машин автопарку є легковими?
2) Вкладник поклав до банку 4000 гривень під 15% річних. Скільки грошей буде на його рахунку через 2 роки?
3) Вартість деякого товару спочатку підвищили на 25 %, а потім знизили на 26%. На скільки відсотків і як змінилась початкова ціна товару?
4) Яку мінімальну суму грошей треба покласти до банку під 10 % річних, щоб через 3 роки отримати більше ніж 50000 грн?